当前位置：首页 > news >正文

用最简单的方式讲述离散傅里叶级数（DFS）以及离散傅立叶变换（DFT）

news 2025/4/18 23:40:10

文章目录

前言

一、傅里叶变换的多种形式

二、浅谈离散傅里叶级数（DFS）

三、浅谈离散傅里叶变换（DFT）

总结

前言

本文对四种不同的傅里叶变换做了总结与梳理，并针对其中存在联系的形式做了推导。接着又讲述了离散傅里叶级数（DFS）的一些特点，可以帮助大家理解离散傅里叶级数（DFS）是如何实现的。最后讲述了我对DFT的一些理解，个人认为有助于理解DFT的作用，知道这些数学工具的本质用途。

一、傅里叶变换的多种形式

首先我们要了解的是四种傅里叶变换形式，以及他们对应的场景

时间函数	频率函数
连续和非周期	非周期和连续
连续和周期	非周期和离散
离散和非周期	周期和连续
离散和周期	周期和离散

1.连续时间信号的傅里叶变换（CTFT）

对于连续时间信号 $f(t)$ ，其傅里叶变换 $F(\omega)$ 定义为：

$F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j \omega t} \, dt$

$f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{j \omega t} \, d\omega$

2.连续周期时间信号的傅里叶级数（FS）

当 $f(t)$ 为连续周期时间信号时，我们可以用傅里叶级数的形式来表示：

将周期为 $T$ 的信号 $f(t)$ 分解为谐波分量：

$c_n = \frac{1}{T} \int_{0}^{T} f(t) e^{-j n \omega_0 t} \, dt$

$c_n$ ：复数形式的傅里叶系数（包含幅度和相位）
$\omega_0 = \frac{2\pi}{T}$ ：基频
$n$ ：谐波次数（n=0,±1,±2,…n=0,±1,±2,…）

用系数 $c_n$ 重建原信号：

$f(t) = \sum_{n=-\infty}^{\infty} c_n e^{j n \omega_0 t}$

至于傅里叶级数的公式是如何由傅里叶变换推导的可以看以下步骤：

① $f(t)$ 是周期为 $T$ 的信号，可以将其表示为非周期信号 $f_0(t)$ 的周期延拓：

$f(t) = \sum_{k=-\infty}^{\infty} f_0(t - kT)$

② 单周期连续时间信号 $f_0(t)$ 的傅里叶变换 $F_0(\omega)$ 计算如下：

$F_0(\omega) = \int_{-T/2}^{T/2} f_0(t) e^{-j \omega t} \, dt$

③ 周期信号的傅里叶变换 $F(\omega)$ 是对 $F_0(\omega)$ 的离散采样，采样频率 $\omega_0 = \frac{2\pi}{T}$ ：

$F(\omega) = \omega_0 \sum_{n=-\infty}^{\infty} F_0(n \omega_0) \delta(\omega - n \omega_0), \quad \omega_0 = \frac{2\pi}{T}$

④ 将 $F(\omega)$ 代入傅里叶逆变换公式，可以知道 $f(t)$ ：

$f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \left( \omega_0 \sum_{n=-\infty}^{\infty} F_0(n \omega_0) \delta(\omega - n \omega_0) \right) e^{j \omega t} \, d\omega$

$f(t) = \frac{1}{T} \sum_{n=-\infty}^{\infty} F_0(n \omega_0) e^{j n \omega_0 t}$

所以式子中的 $\frac{1}{T} F_0(n \omega_0)$ 可以等效理解为级数 $c_n$

3.离散非周期时间信号的序列傅里叶变换（DTFT）

当 $f(t)$ 为离散非周期时间信号时，我们可以用序列傅里叶变换的形式来表示：

$X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x(n) e^{-j\omega n}$

$x(n)= \frac{1}{2\pi} \int_{-\pi}^{\pi} X(e^{j\omega}) e^{j\omega n} \, d\omega$

DTFT可以看作是CTFT的离散时间版本，可以通过以下步骤关联起来：

①时域采样：对连续时间信号 $f(t)$ 以间隔 $T_s$ 采样，得到离散序列 $x(n) = f(n T_s)$

②频谱周期性：采样导致CTFT频谱 $F(\omega)$ 以 $\omega_s = \frac{2\pi}{T}$ 为周期重复（奈奎斯特采样定理）：

$X(e^{j\omega}) = \frac{1}{T_s} \sum_{k=-\infty}^{\infty} F\left(\frac{\omega + 2\pi k}{T_s}\right)$

③归一化频率：定义数字频率 $\omega = \Omega T_s$ ，DTFT的频率范围限制在 $[-\pi, \pi]$

④频域周期性：DTFT的频谱 $X(e^{j\omega})$ 周期为 $2\pi$ ,因为：

$e^{j\omega n} = e^{j(\omega + 2\pi k)n}, \quad k \in \mathbb{Z}$

4.离散周期时间信号的离散傅里叶级数（DFS）

当 $f(t)$ 为离散周期时间信号时，我们则可以使用离散傅里叶级数（DFS）来表示：

$\tilde{X}(k) = \sum_{n=0}^{N-1} \tilde{x}(n) e^{-j \frac{2\pi}{N} kn}, \quad k \in \mathbb{Z}$

$\tilde{x}(n) = \frac{1}{N} \sum_{k=0}^{N-1} \tilde{X}(k) e^{j \frac{2\pi}{N} kn}, \quad n \in \mathbb{Z}$

二、浅谈离散傅里叶级数（DFS）

1.如何理解“无限长序列只有一个周期中的 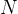$N$ 个序列值有信息”

从DTFT的图中可以看出，如果知道一个周期中 $N$ 个序列值，那么频谱就是周期连续的信号，当时域的序列按照一定周期进行周期延拓时，对应到频域就是对原频域信号进行采样，采样间隔即为 $\frac{2\pi}{N}$ ，所以横坐标 $k$ 对应的数字域频率即为 $\frac{2\pi}{N}k$ 。

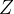2.如何理解“ $\tilde{X}[k]$ 是对 $X(z)$ 在 $Z$ 平面单位圆上采样”

首先通过第一个问题，我们可以知道，周期序列 $\tilde{X}[k]$ 就是对 $\tilde{x}(n)$ 的一个周期 ${x}(n)$ 的DTFT的等间隔采样：

$X(e^{j\omega}) = \sum_{n=0}^{N-1} x(n) e^{-j\omega n} = \sum_{n=0}^{N-1} \tilde{x}(n) e^{-j\omega n}$

$\tilde{X}(k) = X(e^{j\omega}) ,\quad \omega = 2\pi k/N$

同时，因为序列的傅里叶变换是在单位圆上的 $Z$ 变换，而 $z= e^{j\omega}$ 中的数字频率 $\omega=\frac{2\pi}{N}k$ 与所以为了得到 $\tilde{X}[k]$ ，也可以进行对 $X(z)$ 在 $Z$ 平面单位圆上采样：

$\tilde{X}(k) = X(z) ,\quad z= e^{j\omega}=e^{j(\frac{2\pi}{N} )k}$

三、浅谈离散傅里叶变换（DFT）

1.什么是离散傅里叶变换（DFT）

离散傅里叶变换（Discrete Fourier Transform, DFT） 是一种将有限长离散序列从时域转换到频域的数学工具。其核心是将信号分解为一系列有限的复指数谐波的叠加，它将有限长离散信号转换为离散频谱，解决了实际计算问题，公式如下：

$X(K) = \sum_{n=0}^{N-1} x(n )e^{-j \frac{2\pi}{N} kn}, \quad k = 0, 1, \dots, N-1$
$x(n)= \frac{1}{N} \sum_{k=0}^{N-1} X(k) e^{j \frac{2\pi}{N} kn}, \quad n = 0, 1, \dots, N-1$

2.为什么要引入离散傅里叶变换（DFT）

我们可以通过DTFT的时域频域变换图中发现，有限长离散序列的频域应该是周期连续的，然而上图中我们却看到DFT将有限长离散序列的频域用离散且有限的形式表示出来了，这是否矛盾了呢？首先我们应该了解DFT的作用：

①面向解决实际计算问题：在实际生活中我们面临的都是模拟域的连续信号，但是当我们需要用计算机计算时，却只能通过数字采样后对它的离散序列进行处理。

②弥补DTFT对计算机运算的不足：离散时间傅里叶变换（DTFT）虽然适用于离散信号，但输出是连续频谱 $X(e^{j\omega})$ ，无法直接用计算机存储或计算。DFT通过离散化频域，生成有限个频率点 ${X}(k)$ ，实现数值计算。

对于DFT的意义，我认为可以理解为是便于计算机运算的傅里叶变换（FS），也就是说对于想使用计算机来处理模拟域连续信号的我们来说，我们只能尽可能地用离散化的数值来还原出信号在模拟域中原本的摸样，而DFT就是为实现这种目的而专门为计算机设计而出的特殊计算方式。

总结

大半年没有更新博客，这次更新居然是和专业课相关的内容。至于为什么会写一篇关于傅里叶变换的博客，完全是因为自己在大三下这个学期再修数字信号处理时，又一次被这些乱七八糟的变换公式骚扰到，一怒之下猛花一天梳理完这部分内容。不过写完这篇博客后思路确实清晰了不少，虽然内容涉及的不多，有些内容也没有分析地很深入，但是在一定程度上应该可以帮助到大家理解，但愿对大家有所帮助。

查看全文

http://www.mrgr.cn/news/97910.html