【NLP 面经 9.逐层分解Transformer】
目录
一、Transformer 整体结构
1.Tranformer的整体结构
2.Transformer的工作流程
二、Transformer的输入
1.单词 Embedding
2.位置 Embedding
计算公式:
三、Self-Attention 自注意力机制
1.Self-Attention 结构
编辑
2.Q、K、V的计算
代码实现
3.Self-Attention 的输出
4.Multi-Head Attention
5.代码实现
Ⅰ、类定义与初始化
Ⅱ、线性投影层定义
Ⅲ、前向传播过程
① 输入张量分割多头
② 注意力分数计算
四、Encoder 结构
1.Add & Norm
2.Feed Forward
3.组成 Encoder
五、Decoder 结构
1.第一个 Multi-Head Attention
第四步:
第五步:
2.第二个 Multi-Head Attention
3.Softmax 预测输出单词
六、Transformer 总结
如果我能给你短暂的开心
—— 25.4.7
一、Transformer 整体结构
1.Tranformer的整体结构
Transformer 的整体结构,左图Encoder和右图Decoder,下图是Transformer用于中英文翻译的整体结构:

可以看到 Transformer 由 Encoder 和 Decoder 两个部分组成,Encoder 和 Decoder 都包含 6 个 block
2.Transformer的工作流程
第一步:获取输入句子的每一个单词的表示向量 X,X 由单词的 Embedding(Embedding就是从原始数据中提取出来的特征 Feature)和单词位置的 Embedding 相加得到

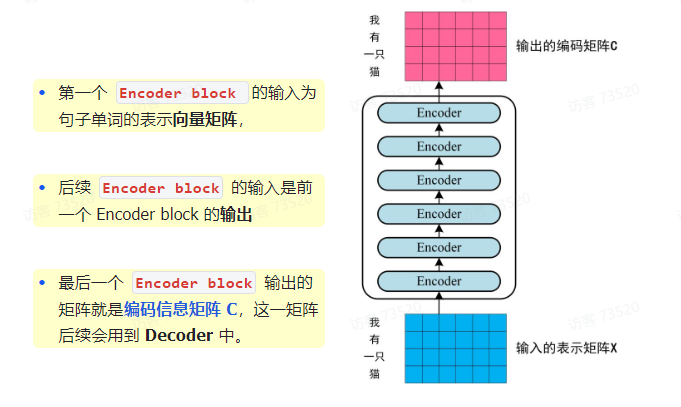
第二步:将得到的单词表示向量矩阵(如上图所示,每一行是一个单词的表示 x)传入 Encoder 中,经过 6 个 Encoder block 后可以得到句子所有单词的编码信息矩阵 C
如下图,单词向量矩阵用 X_(n × d) 表示,n 是句子中单词个数,d 是表示向量的维度(d = 512).每一个 Encoder block 输出的矩阵维度与输入完全一致

第三步:将 Encoder 输出的编码信息矩阵 C 传递到 Decoder 中,Decoder 依次会根据当前翻译过的单词 1 ~ i 翻译下一个单词 i + 1,如下图所示,在使用的过程中,翻译到单词 i + 1 时候需要通过 Mask(掩盖)操作遮盖住 i + 1 之后的单词

上图 Decoder 接收了 Encoder 的编码矩阵 C,然后首先输入一个翻译开始符 "<Begin>",预测第一个单词 "I";然后输入翻译开始符 "<Begin>" 和单词 "I”,预测单词 "have",以此类推。这是 Transformer 使用时候的大致流程,接下来是里面各个部分的细节
二、Transformer的输入
Transformer 中单词的输入表示 x 由 单词 Embedding 和 位置 Embedding(Positional Encoding)相加得到

1.单词 Embedding
单词的 Embedding 有很多种方式可以获取,例如可以采用 Word2Vec、Glove 等算法预训练得到,也可以在 Transformer 中训练得到
2.位置 Embedding
Transformer 中除了单词的 Embedding,还需要使用 位置Embedding 表示单词出现在句子中的位置。因为 Transformer 不采用 RNN 的结构,而是使用全局信息,不能利用单词的顺序信息,而这部分信息对于 NLP 来说非常重要。所以 Transformer 中使用 位置Embedding 保存单词在序列中的相对或绝对位置。
位置 Embedding 用 PE 表示,PE 的维度与单词 Embedding 是一样的,PE可以通过训练得到,也可以使用某种公式计算得到,在Transformer中采用了后者,使用公式计算得到
计算公式:

其中,pos 表示单词在句子中的位置,d 表示 PE 的维度(与词Embedding一样),2i 表示偶数的维度,2i + 1 表示奇数的维度(即 2i ≤ d,2i + 1 ≤ d)。使用这种公式计算 PE 有以下好处:
① 使 PE 能够适应比训练集里面所有句子更长的句子,假设训练集里面最长的句子是有20个单词,突然来了一个长度为21的句子,则是用公式计算的方法可以计算出第21位的 Embedding
② 可以让模型容易地计算出相对位置,对于固定长度的间距 k,PE(pos + k) 可以用 PE(pos) 计算得到,因为:sin(A+B) = sin(A) * cos(B) + cos(A) * sin(B),cos(A + B) = cos(A) * cos(B) - sin(A) * sin(B)
三、Self-Attention 自注意力机制
Transformer的内部结构图:
左侧为 Encoder block
右侧为 Decoder block
红色圈中的部分为 Multi-Head Attention,是由多个 Self-Attention 组成的

Encoder block 包含一个 Multi-Head Attention
Decoder block 包含两个 Multi-Head Attention(其中有一个用到Masked)
Multi-Head Attention 上方还包括一个 Add & Norm 层
Add 表示残差链接(Residual Connection)用于防止网络退化
Norm 表示 Layer Normalization,用于对每一层的激活值进行归一化
因为 Self-Attention 是 Transformer 的重点,所以我们重点关注 Multi-Head Attention 以及 Self-Attention
1.Self-Attention 结构
上图是 Self-Attention 的结构,在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。在实际中,Self-Attention 接收的是输入(单词的表示向量 x 组成的矩阵 X)或者上一个Encoder block的输出,而Q,K,V正是通过 Self-Attention 的输入进行线性变换得到的
2.Q、K、V的计算
Self-Attention 的输入用矩阵 X表示,则可以使用线性变换矩阵 W_Q、W_K、W_V 计算得到Q、K、V,计算如下图所示:注意,X、Q、K、V 的每一行都表示一个单词

代码实现
nn.Linear():实现全连接层的线性变换,计算公式为 y = xA^T + b,其中 A 是权重矩阵,b 是偏置项。适用于输入输出的最后一维特征变换,支持任意维度输入(如2D、3D张量),仅对最后一维进行线性映射
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
in_features | int | 是 | - | 输入张量最后一维的特征数(如输入形状 (batch, 20),则 in_features=20) |
out_features | int | 是 | - | 输出张量最后一维的特征数(如输出形状 (batch, 30),则 out_features=30) |
bias | bool | 否 | True | 是否添加可学习的偏置项。若设为 False,则 y = xA^T。 |
.permute():调整张量的维度顺序,不改变数据内容,仅重新排列轴顺序。例如将形状 (batch, height, width, channel) 转换为 (batch, channel, height, width),常用于适配不同层的数据格式(如CNN输入与全连接层的对接)
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
dims | int 可变参数 | 是 | - | 新维度的顺序,需指定所有维度索引(如原维度顺序是 (0,1,2),调用 .permute(2,0,1) 后变为 (2,0,1)) |
nn.Softmax():概率归一化,对输入张量的指定维度(dim)进行指数运算,然后归一化到 [0, 1] 区间,使得该维度所有元素的和为 1。输出结果可解释为不同类别的概率。
| 参数名 | 类型 | 可选性 | 说明 | 默认值 |
|---|---|---|---|---|
dim | int | 必选 | 指定计算 Softmax 的维度。例如输入为 3D 张量时,dim=-1 表示对最后一维操作。 | 必填,无默认 |
torch.matmul(): PyTorch 中用于执行张量矩阵乘积的核心函数,支持多维张量的批量计算和广播机制。
| 参数名 | 类型 | 是否可选 | 说明 | 默认值 |
|---|---|---|---|---|
input | torch.Tensor | 必选 | 第一个输入张量,支持 1D/2D/高维张量。 | - |
other | torch.Tensor | 必选 | 第二个输入张量,需与 input 的最后两维满足矩阵乘法规则。 | - |
out | torch.Tensor | 可选 | 指定输出张量,用于存储计算结果。 |
torch.bmm():执行批量矩阵乘法,适用于三维张量(形状为 (batch, n, m) 和 (batch, m, p)),逐个批次计算两个矩阵的乘积。常用于注意力机制中的 Q*K^T 操作或全连接层的批量并行计算
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
input | Tensor | 是 | - | 输入张量,形状为 (batch, n, m),每个批次包含一个 n×m 矩阵。 |
mat2 | Tensor | 是 | - | 输入张量,形状为 (batch, m, p),每个批次包含一个 m×p 矩阵。 |
out | Tensor | 否 | None | 可选输出张量,用于存储结果,形状为 (batch, n, p)。 |
import numpy as np
from math import sqrt
import torch
from torch import nnclass Self_Attention(nn.Module):# input: batch size * seq_len * input_dim# q: (batch size, input_dim, dim k)# k: (batch_size, input_dim, dim k)# v: (batch size, input_dim, dim_v)def __init__(self, input_dim, dim_k, dim_v):super(Self_attention, self).__init__:self.q = nn.Linear(input_dim, dim_k)self.k = nn.Linear(input_dim, dim_k)self.v = nn.Linear(input_dim, dim_v)self.__norm_fact = 1 / sqrt(dim_k)def forward(self, x):Q = self.q(x) # Q: (batch_size, seq_len, dim_k)K = self.k(x) # K: (batch_size, seq_len, dim_k)V = self.v(x) # V: (batch_size, seq_len, dim_v)# Q * K.T(): (batch_size, seq_len, seq_len)# Q: (batch_size, seq_len, dim_k)# K: (batch_size, seq_len, dim_k)# K.permute(0, 2, 1): (batch_size, dim_k, seq_len)attn_scores = torch.matmul(Q, K.permute(0, 2, 1)) # Q·K^Tattn_scores = attn_scores * self.__norm_fact # 缩放attn = nn.Softmax(dim=-1)(attn_scores) # Softmax归一化# Q * K.T() * V: batch_size * seq_len * dim_voutput = torch.bmm(attn, v)return outputX = torch.randn(4, 3, 2) # 输入维度:(batch=4, seq=3, input_dim=2)
print(X)
self_attn = Self_Attention(2, 4, 5) # input_dim:2 k_dim: 4 v_dim: 5
res = self_attn(X)
print(res.shape) # [4, 3, 5]3.Self-Attention 的输出
得到矩阵 Q、K、V 之后就可以计算出 Self-Attention 的输出了,计算的公式如下:

公式中计算矩阵 Q 和 K 每一行向量的内积,为了防止内积过大,因此除以 d_k 的平方根。Q乘以K的转置后,得到的矩阵行列数都为 n,n 为句子单词数,这个矩阵可以表示单词之间的 attention 强度。下图为 Q 乘以 K_T,1 2 3 4表示的是句子中的单词

得到 Q * K_T 之后,使用 Softmax 计算每一个单词对于其他单词的 attention 系数,公式中的 Softmax 是对矩阵的每一行进行 Softmax,即每一行的和都变为1

得到 Softmax 矩阵之后可以和 V 相乘,得到最终的输出 Z

上图中 Softmax 矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数,最终单词 1 的输出 Z1 等于所有单词 i 的值 V_i,根据 attention 系数的比例加在一起得到,如下图所示:

4.Multi-Head Attention
在上一步,我们已经知道怎么通过 Self-Attention 计算得到输出矩阵 Z,而 Multi-Head Attention 是由多个 Self-Attention 组合形成的,下图是论文中 Multi-Head Attention 的结构图

从上图可以看到 Multi-Head Attention 包含多个 Self-Attention 层,首先将输入 X 分别传递到 h 个不同的 Self-Attention 中,计算得到 h 个输出矩阵 Z。下图是 h = 8 时候的情况,此时会得到 8 个输出矩阵 Z

得到 8 个输出矩阵,Z1 到 Z8 之后,Multi-Head Attention 将它们拼接在一起(Concat),然后传入一个 Linear 层,得到 Multi-Head Attention 最终的输出 Z

可以看到 Multi-Head Attention 输出的矩阵 Z 与其输入的矩阵 X 的维度是一样的
5.代码实现
Ⅰ、类定义与初始化
input_dim:输入特征维度(如词向量维度)
dim_k:总键/查询维度(需被头数整除)
dim_v:总价值维度(需被头数整除)
nums_head:注意力头数
class Self_Attention_Muti_Head(nn.Module):def __init__(self, input_dim, dim_k, dim_v, nums_head):super(Attention_Muti_Head, self).__init__()assert dim_k % nums_head == 0 # 确保dim_k可被头数整除assert dim_v % nums_head == 0 # 确保dim_v可被头数整除Ⅱ、线性投影层定义
输入:(batch_size, seq_len, input_dim)
Q输出:(batch_size, seq_len, dim_k)
K输出:(batch_size, seq_len, dim_k)
V输出:(batch_size, seq_len, dim_v)
nn.Linear():对输入数据执行线性变换 y=xA^T+b,常用于神经网络的特征映射和分类层
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
in_features | int | 是 | 无 | 输入特征维度(如BERT隐藏层768) |
out_features | int | 是 | 无 | 输出特征维度(如词汇表30522) |
bias | bool | 否 | True | 是否启用偏置项 |
device | str | 否 | None | 张量存储设备(CPU/GPU) |
dtype | dtype | 否 | None | 张量数据类型(如float32) |
# q: batch_size , input_dim , dim_kself.q = nn.Linear(input_dim, dim_k) # Q线性变换层# k: batch_size , input_dim , dim_kself.k = nn.Linear(input_dim, dim_k) # K线性变换层# v: batch_size , input_dim , dim_vself.v = nn.Linear(input_dim, dim_v) # V线性变换层Ⅲ、前向传播过程
① 输入张量分割多头
输入 x:(batch_size, seq_len, input_dim)
分割后Q:(num_heads, batch_size, seq_len, dim_k//nums_head)
分割后K:(num_heads, batch_size, seq_len, dim_k//nums_head)
分割后V:(num_heads, batch_size, seq_len, dim_v//nums_head)
张量.reshape():在不改变数据顺序的前提下调整张量维度,支持自动推断维度(-1)
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
shape | tuple 或 int | 是 | 无 | 目标形状(如(6, -1)) |
张量.shape:返回张量的维度信息元组,如 (batch_size, seq_len, hidden_dim)
# x: batch_size, seq_len, input_dimdef forward(self, x):# Q: batch_size, seq_len, dim_kQ = self.q(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head)# K: batch_size, seq_len, dim_kK = self.k(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head)# V: batch_size, seq_len, dim_vV = self.v(x).reshape(-1, x.shape[0], x.shape[1], self.dim_v // self.nums_head)② 注意力分数计算
输入Q:(num_heads, batch, seq, d_k)
输入K:(num_heads, batch, seq, d_k)
输出attn_scores:(num_heads, batch, seq, seq)
nn.Softmax():将输入转换为概率分布(总和为1),常用于分类任务
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
dim | int | 否 | -1 | 应用Softmax的维度索引 |
torch.matmul():支持多维张量的矩阵乘法,包含广播机制
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
input | Tensor | 是 | 无 | 输入张量(如矩阵A) |
other | Tensor | 是 | 无 | 输入张量(如矩阵B) |
out | Tensor | 否 | None | 输出张量(可选) |
permute():重新排列张量的维度顺序,常用于处理图像或序列数据
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
dims | int序列 | 是 | 无 | 新维度顺序(如(2,0,1)) |
# batch_size, num_heads, seq_len, seq_lenattn_scores = (torch.matmul(Q, K, permute(0, 1, 3, 2))attn_weights = nn.Softmax(dim = -1)(attn_scores)# Q: batch_size * num_heads * seq_len * d_k# K.T():batch_size * num_heads * d_k * seq_len# Q * K.T(): batch_size * seq_len * seq_len张量.size():返回张量的维度信息(与.shape等效)或指定维度的长度
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
dim | int | 否 | None | 指定维度索引(可选) |
torch.rand():生成区间 [0,1) 内均匀分布的随机数张量
| 参数名 | 类型 | 必选 | 默认值 | 说明 |
|---|---|---|---|---|
size | tuple 或 int | 是 | 无 | 张量形状(如(2,3)) |
dtype | dtype | 否 | None | 数据类型(如torch.float32) |
device | str | 否 | None | 存储设备(如'cuda') |
# Muti-head Attention 机制的实现
from math import sqrt
import torch
import torch.nn as nn
from torch import permuteclass Self_Attention_Multi_Head(nn.Module):# 输入张量维度 input: (batch_size , seq_len , input_dim)def __init__(self, input_dim, dim_k, dim_v, nums_head):super(Self_Attention_Multi_Head, self).__init__()assert dim_k % nums_head == 0 # 确保dim_k可被头数整除assert dim_v % nums_head == 0 # 确保dim_v可被头数整除# q: (batch_size , input_dim , dim_k)self.q = nn.Linear(input_dim, dim_k) # Q线性变换层# k: (batch_size , input_dim , dim_k)self.k = nn.Linear(input_dim, dim_k) # K线性变换层# v: (batch_size , input_dim , dim_v)self.v = nn.Linear(input_dim, dim_v) # V线性变换层self.nums_head = nums_head # 头数self.dim_k = dim_k # 总键维度self.dim_v = dim_v # 总值维度self._norm_fact = 1 / sqrt(dim_k) # 缩放因子# x: (batch_size, seq_len, input_dim)def forward(self, x):# Q: (batch_size, seq_len, dim_k)Q = self.q(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head)# 实际维度:(num_heads, batch_size, seq_leng, head_dim)# K: batch_size, seq_len, dim_kK = self.k(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head)# V: batch_size, seq_len, dim_vV = self.v(x).reshape(-1, x.shape[0], x.shape[1], self.dim_v // self.nums_head)print(x.shape)print(Q.size())# batch_size, num_heads, seq_len, seq_len# Q * K.T(): batch_size * num_heads * seq_len * seq_lenattn_scores = nn.Softmax(dim=-1)(torch.matmul(Q, K.permute(0, 1, 3, 2)))# Q: batch_size * num_heads * seq_len * d_k# K.T():batch_size * num_heads * d_k * seq_len# Q * K.T(): batch_size * seq_len * seq_lenoutput = torch.matmul(attn_scores, V).reshape(x.shape[0], x.shape[1], -1)# Q * K.T() * V: (batch_size * seq_len * dim_v)return outputx = torch.rand(1, 3, 4)
print(x)
attn = Self_Attention_Multi_Head(input_dim=4, dim_k=4, dim_v=4, nums_head=2)
y = attn(x)
print(y.shape) # 输出 torch.Size([1, 3, 4])四、Encoder 结构

蓝色部分是 Transformer 的 Encoder block 结构,可以看到是由 Multi-Head Attention、Add & Norm、Feed Forward组成的,上文介绍了 Multi-Head Attention 的计算过程,现在了解一下 Add & Norm 和 Feed Forward 部分
1.Add & Norm
Add & Norm 层由 Add 和 Norm 两部分组成,其计算公式如下:

其中 X 表示 Multi-Head Attention 或者 Feed Forward 的输入,MultiHeadAttention(X) 和 FeedForward(X) 表示输出(输出与输入 X 维度是一样的,所以可以相加)
Add 指 X + Multi Head Attention(X),是一种残差连接,通常用于解决多层网络训练的问题,可以让网络只关注当前差异的部分,在 ResNet 中经常用到

Norm 指 Layer Normalization,通常用于 RNN 结构,Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的,这样可以加快收敛
2.Feed Forward
Feed Forward 层比较简单,是一个两层的全连接层,第一层的激活函数为 Relu,第二层不使用激活函数,对应的公式如下:

X 是输入,Feed Forward 最终得到的输出矩阵的维度与 X 一致
3.组成 Encoder
通过上面描述的 Multi-Head Attention,Feed Forward,Add & Norm 就可以构造出一个 Encoder block,Encoder block 接收输入矩阵 X_(n × d),并输出一个矩阵 O_(n × d)。通过多个 Encoder block 叠加就可以组成 Encoder
五、Decoder 结构

Transformer Decoder block
红色部分为 Transformer 的 Decoder block 结构,与 Encoder block 相似,但是存在一些区别:
① 包含两个 Multi-Head Attention 层
② 第一个 Multi-Head Attention 层采用了 Masked 操作
③ 第二个 Multi-Head Attention 层的 K,V 矩阵使用 Encoder 的编码信息矩阵C进行计算,而 Q 使用上一个 Decoder block 的输出计算
④ 最后有一个 Softmax 层计算下一个翻译单词的概率
1.第一个 Multi-Head Attention
Decoder block 的第一个 Multi-Head Attention 采用了 Masked 操作,因为在翻译的过程中是顺序翻译的,即翻译完第 i 个单词,才可以翻译第 i + 1 个单词。通过 Masked 操作可以防止第 i 个单词知道 i + 1 个单词之后的信息。下面以 “我有一只猫” 翻译成 “I have a cat” 为例,了解一下 Masked 操作
在 Decoder 的时候,是需要根据之前的翻译,求解当前最有可能的翻译,如下图所示,首先根据输入 “<Begin>” 预测出第一个单词为 “I”,然后根据输入 “<Begin> I” 预测下一个单词 “have”。

Decoder 可以在训练的过程中使用 Teacher Forcing 并且并行化训练,即将正确的单词序列 (<Begin> I have a cat)和对应输出(I have a cat <end>) 传递到 Decoder。那么在预测第 i 个输出时,就要将第 i + 1 之后的单词掩盖住
注意 Mask 操作是在 Self-Attention 的 Softmax 之前使用的,下面用 0 1 2 3 4 5 分别表示 <Begin> I have a cat <end>。
第一步:下图是 Decoder 的输入矩阵 和 Mask 矩阵,输入矩阵包含 “<Begin> I have a cat"(0 1 2 3 4 5)五个单词的表示向量,Mask 是一个 5 × 5 的矩阵。在 Mask 可以发现单词 0 只能使用单词 0 的信息,而单词 1 可以使用单词 0、1的信息,即只能使用之前的信息

第二步:接下来的操作和之前的 Self-Attention 一样,通过输入矩阵 X 计算得到 Q、K、V矩阵,然后计算 Q 和 K^T 的乘积 QK^T

第三步:在得到 QK^T之后,需要进行 Softmax,计算 attention score,我们在 Softmax 之前需要使用 Mask 矩阵遮挡住每一个单词之后的信息,遮挡操作如下:

得到 Mask QK^T,之后在 Mask QK^T 上进行 Softmax,每一行的和都为 1,但是单词 0 在 单词 1,2,3,4 上的 attentionn score 都为 0
第四步:
4.使用 Mask Q * K^T 与 矩阵V 相乘,得到输出 Z,则单词 1 的输出向量 Z_1 是只包含单词 1 的信息的

第五步:
5.通过上述步骤就可以得到一个 Mask Self-Attention 的输出矩阵 Z_i,然后和 Encoder 类似,通过 Multi-Head Attention 拼接多个输出 Z_i,然后计算得到第一个 Multi-Head Attention 的输出 Z,Z 与 输入X维度一样
2.第二个 Multi-Head Attention
Decoder block 第二个 Multi-Head Attention 变化不大,主要的区别在于其中 Self-Attention 的 K、V 矩阵不是使用上一个 Decoder block 的输出计算的,而是使用 Encoder 的编码信息矩阵 C 计算的
根据 Encoder 的输出 C 计算得到 K、V,根据上一个 Decoder block 的输出 Z 计算 Q(如果是第一个 Decoder block,则使用输入矩阵 X 进行计算),后续的计算方法与之前描述的一致
这样做的好处是在 Decoder 的时候,每一位单词都可以利用到 Encoder 所有单词的信息(这些信息无需 Mask)。
3.Softmax 预测输出单词
Decoder block 最后的部分是利用 Softmax 预测下一个单词,在之前的网络层我们可以得到一个最终的输出 Z,因为 Mask 的存在,使得 单词 0 的输出 Z_0 只包含单词 0 的信息,如下:

Softmax 根据输出矩阵的每一行预测下一个单词:

这就是 Decoder block 的定义,与 Encoder 一样,Decoder 是由多个 Decoder block 组合而成
六、Transformer 总结
1.Transformer 与 RNN 不同,可以比较好的并行训练。
2.Transformer 本身是不能利用单词的顺序信息的。因此需要在输入中添加位置 Embedding,否则 Transformer 就是一个词袋模型了。
3.Transformer 的重点是 Self-Attention 结构,其中用到的 Q、K、V 矩阵通过输出进行线性变换得到。
4.Transformer 中 Multi-Head Attention 中有多个 Self-Attention,可以捕获单词之间多种维度上的相关系数 attention score。

