强化学习算法系列（一）：动态规划方法——策略迭代算法(PI)与值迭代算法(VI)

强化学习算法

（一）动态规划方法——策略迭代算法(PI)和值迭代算法(VI)
（二）Model-Free类方法——蒙特卡洛算法(MC)和时序差分算法(TD)
（三）基于动作值的算法——Sarsa算法与Q-Learning算法
（四）深度强化学习时代的到来——DQN算法
（五）最主流的算法框架——AC算法（AC、A2C、A3C、SAC）
（六）应用最广泛的算法——PPO算法与TRPO算法
（七）更高级的算法——DDPG算法与TD3算法
（八）待续

---

---

前言

本章将会介绍策略迭代算法和值迭代算法这两个最基础的强化学习算法，两种算法均属于动态规划方法。从这两种算法开始学习可以对强化学习的核心理论有更深入的认识。此外，在这篇博客中将会对算法中的一些疑难问题做出个人的一些理解注释，如有不准确的地方请评论指出，万分感谢！

---

一、策略迭代算法

1. 核心思想

策略迭代算法（Policy Iteration，PI） 首先需要初始化策略${\pi }_0$，评估当前策略$\pi$的状态价值$V^{\pi }(s)$，根据状态价值$V^{\pi }(s)$更新策略，直至策略$\pi$收敛。因此策略迭代算法由两大部分构成，分别为策略评估和策略改进。

• 策略评估（Policy Evaluation）
  该过程基于贝尔曼方程完成，用于计算当前策略$\pi$的状态该价值函数，其公式为
  $$V^{\pi }(s)\leftarrow \sum _a\pi (a\mid s)[R(s,a)+\gamma \sum _{s^{\prime }}P(s\prime \mid s,a)V^{\pi }(s^{\prime })]$$
• 策略改进（Policy Improvement）
  根据当前的状态价值函数更新策略，即每处状态的动作均选择动作价值最大的（贪婪选择），其公式为
  $${\pi }_{new}(s)\leftarrow \underset{a}{\mathrm{argmax}}[R(s,a)+\gamma \sum _{s^{\prime }}P(s\prime \mid s,a)V^{\pi }(s^{\prime })]$$

个人理解：策略迭代算法的原理比较简单，我们可以以网格化的迷宫问题为例理解这一算法。
现在想要找到从起点找到终点的最短路径。在策略迭代算法的开始时，我们在每格网格上为每个方向（假定只有前后左右四个方向）的动作随机设定一定的概率，然后带入上述策略评估的贝尔曼方程对初始策略进行评估，这时我们得到了基于初始策略的状态价值。根据状态价值带入策略改进的公式计算每处网格的最大价值动作，并将该动作做为改进后的策略。按照这一过程不断迭代，每次策略改进都会使得策略变得不劣于之前的策略。对于有限状态空间问题，策略的改进过程不可能无限进行，因此算法一定会在有限步内收敛到最优策略。

2. 代码实战

下面是一个4*4网格化迷宫问题的代码实验，注释中有我碰到的一些问题和解释。

import numpy as np
import matplotlib.pyplot as plt# 定义网格世界参数
GRID_SIZE = 4
STATES = GRID_SIZE * GRID_SIZE
ACTIONS = 4  # 上(0)、右(1)、下(2)、左(3)
GAMMA = 0.9  # 折扣因子
EPSILON = 1e-4  # 收敛阈值
# 终点(3,3)，障碍物(1,1)
GOAL = (3, 3)
OBSTACLE = (1, 1)
# 动作对应的坐标变化
ACTION_DELTA = [(-1, 0), (0, 1), (1, 0), (0, -1)]  # 上、右、下、左# 环境模型构建：初始化状态转移矩阵与奖励函数
def build_model():"""这里直接用状态转移矩阵表示环境了，也可以不用。不过那样得每次重新计算在某一状态下选取动作的下一状态，这种是提前算出来所有的了。下面的R和状态转移矩阵类似也是提前初始化全部每步奖励后面学习DQN算法或者别的深度强化学习算法时拟合的就是类似这种R，这里算是提前感受一下。"""# P(s,a,s')为状态转移矩阵，用三维矩阵的形式表示# 其值表示即在某一状态选择某一动作会到达哪一状态？P = np.zeros((STATES, ACTIONS, STATES))# R(s,a)为奖励函数奖励函数，生成一个STATES*ACTIONS的二维矩阵# 矩阵元素用-1填充，因为默认每步奖励为-1R = np.full((STATES, ACTIONS), -1.0)  # 默认每步奖励-1# 遍历每一状态for s in range(STATES):x, y = s // GRID_SIZE, s % GRID_SIZEif (x, y) == GOAL:continue  # 终点无动作# 遍历每一状态下的每一动作for a in range(ACTIONS):dx, dy = ACTION_DELTA[a]x_next = x + dxy_next = y + dy# 检查边界if x_next < 0 or x_next >= GRID_SIZE or y_next < 0 or y_next >= GRID_SIZE:x_next, y_next = x, y  # 碰壁保持原位# 障碍物阻挡if (x_next, y_next) == OBSTACLE:x_next, y_next = x, ys_next = x_next * GRID_SIZE + y_next# 更新转移概率P[s, a, s_next] = 1.0  # 确定性转移# 到达终点的奖励为0if (x_next, y_next) == GOAL:R[s, a] = 0.0return P, R# 策略迭代算法
def policy_iteration(P, R, gamma=GAMMA, epsilon=EPSILON):policy = np.random.randint(0, ACTIONS, size=STATES)  # 初始随机策略V = np.zeros(STATES)policy_history = [policy.copy()]  # 记录策略变化while True:# 一、策略评估while True:V_prev = V.copy()for s in range(STATES):a = policy[s]V[s] = R[s, a] + gamma * np.sum(P[s, a] * V)# 问题（一）if np.max(np.abs(V - V_prev)) < epsilon:break# 二、策略改进policy_stable = Truefor s in range(STATES):old_action = policy[s]Q = np.sum(P[s] * (R[s].reshape(-1, 1) + gamma * V), axis=1)policy[s] = np.argmax(Q)# 改进到找不到更好的策略为止：# old_action != policy[s]：如果旧策略与新策略不一样，说明新策略做出了改进，仍有改进空间，需要重新评估策略；# old_action = policy[s]：新旧策略一样，说明已经没有改进空间了，policy_stable = True，结束算法。if old_action != policy[s]:policy_stable = Falsepolicy_history.append(policy.copy())if policy_stable:breakreturn V, policy, policy_history# 绘图函数——每个状态价值
def plot_value(V, title):plt.figure(figsize=(8, 6))grid = V.reshape((GRID_SIZE, GRID_SIZE))# 绘制网格和状态值plt.imshow(grid, cmap='viridis', origin='upper')plt.colorbar()plt.title(title)# 标注特殊状态for i in range(GRID_SIZE):for j in range(GRID_SIZE):if (i, j) == GOAL:plt.text(j, i, 'GOAL', ha='center', va='center', color='white')elif (i, j) == OBSTACLE:plt.text(j, i, 'BLOCK', ha='center', va='center', color='white')else:plt.text(j, i, f'{V[i * GRID_SIZE + j]:.1f}', ha='center', va='center', color='white')plt.xticks([])plt.yticks([])plt.show()# 绘图函数——最优策略，即每个状态的最优动作
def plot_policy(policy, title):plt.figure(figsize=(8, 6))action_symbol = ['↑', '→', '↓', '←']for i in range(GRID_SIZE):for j in range(GRID_SIZE):s = i * GRID_SIZE + jif (i, j) in [GOAL, OBSTACLE]:plt.text(j, i, 'GOAL' if (i, j) == GOAL else 'BLOCK', ha='center', va='center')else:plt.text(j, i, action_symbol[policy[s]], ha='center', va='center', fontsize=20)plt.xlim(-0.5, GRID_SIZE - 0.5)plt.ylim(-0.5, GRID_SIZE - 0.5)plt.gca().invert_yaxis()plt.title(title)plt.grid(True)plt.show()if __name__ == '__main__':P, R = build_model()V_pi, policy_pi, policy_history = policy_iteration(P, R)plot_value(V_pi, "Policy Iteration - Optimal State Values")plot_policy(policy_pi, "Policy Iteration - Optimal Policy")

问题（一）：这里是我困惑很久的地方，现在有些清楚了，按我的理解解释一下：我们对策略评估的标准就是状态价值，状态价值的计算方法就是贝尔曼方程。而贝尔曼方程我们有以下三种求解方式，简单分析一下。
①原始定义求解：即每处状态采取动作的奖励乘以折扣因子的累次幂再累加得到，低效。
②逆矩阵求解：列出当前策略下所有状态的贝尔曼方程，并化简，我们会得到一个STATES元一次方程组，利用逆矩阵的方式求解这一方程组，我们可以直接得到所有状态的价值，但是逆矩阵求解会随维度（STATES）的提升，复杂度激增。
③BootStrapping思想（自举法）：当前的估计值（或部分已知信息）来更新自身，而非完全依赖外部反馈或完整轨。利用已知自身价值和外部奖励迭代逐渐逼近真实的状态价值，这在计算机世界中很容易实现，因此强化学习领域中多采用该方法。
问题（二）：状态转移矩阵与策略
策略是智能体的决策规则，定义在状态 s 下选择动作 a 的方式。可以是：
​确定性策略：$\pi (s)=a$，直接指定动作。
​随机性策略：$\pi (a\mid s)$，选择动作的概率分布。
​状态转移矩阵：$P(s’\mid s,a)$，描述环境动态的数学模型，表示在状态 s 执行动作 a 后，转移到状态 s 的概率。
状态转移矩阵是由环境确定、固定的，策略是可以改变的。

运行结果：

---

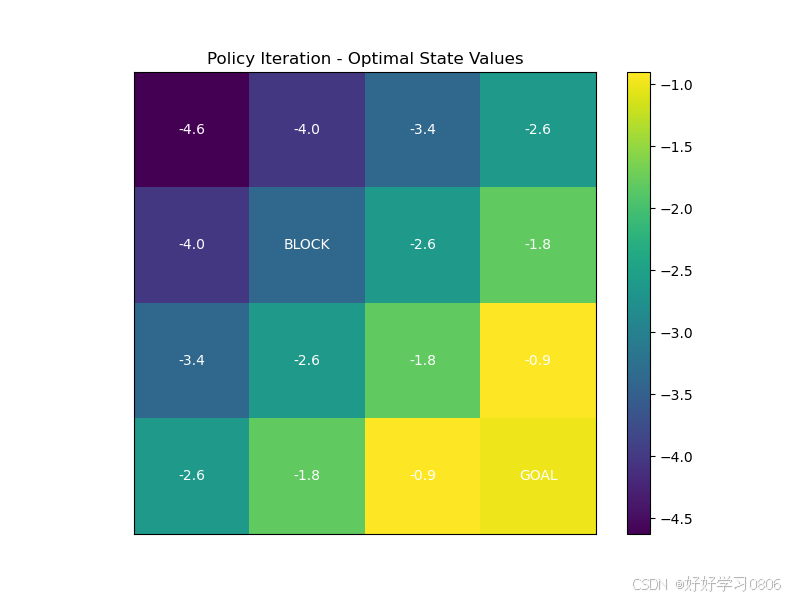
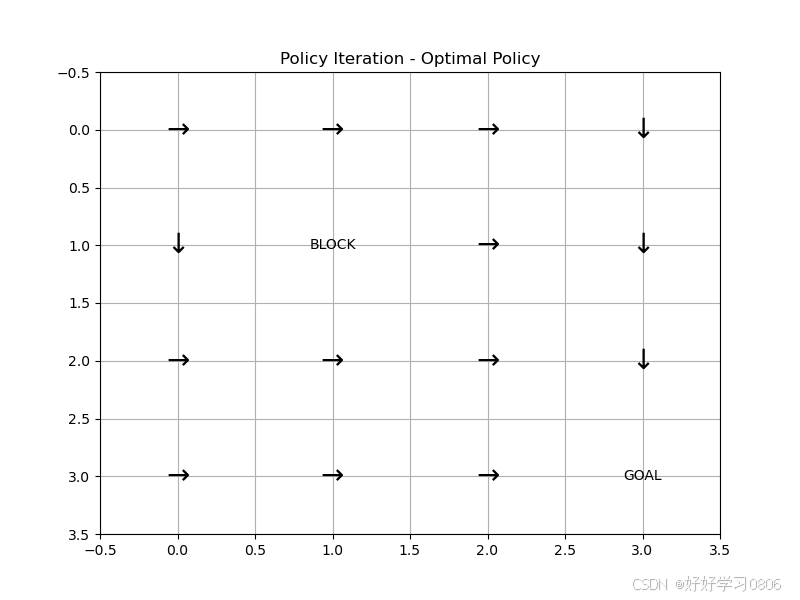
二、值迭代算法

1. 核心思想

值迭代算法（Value Iteration，VI）通过贝尔曼最优方程直接迭代更新价值函数$V(s)$，直至收敛到最优价值函数$V^{\ast }(s)$，在从中提取最优策略${\pi }^{\ast }$。值迭代算法利用了贝尔曼最优方程能够直接跳出对具体策略依赖的特性，将状态价值直接与最优动作挂钩。这里隐含了一个关键点，即在最优策略下，每个状态的动作选择都是当前最优的。我们可以一句话总结值迭代算法的核心思想：在每一状态都直接逼近最优状态价值，得到的策略就是最优策略。将贝尔曼最优方程表示为：
$$V_{k+1}(s)\leftarrow \underset{a}{\max }[R(s,a)+\gamma \sum _{s^{\prime }}P(s\prime \mid s,a)V_k(s^{\prime })]$$

这里仍以网格迷宫为例说一下个人理解，在初始时所有状态价值均为0，按照贝尔曼最优方程计算能够得到最大状态价值的动作，在初次迭代后终点附近的网格能够先找到最优的动作，而其他位置的网格没有找到，但随着迭代的进行，各处的网格都能找到最优的动作了。

2. 代码实战

此处代码和策略迭代算法的代码为同一模型，方便阅读。

import numpy as np
import matplotlib.pyplot as plt# 定义网格世界参数
GRID_SIZE = 4
STATES = GRID_SIZE * GRID_SIZE
ACTIONS = 4  # 上(0)、右(1)、下(2)、左(3)
GAMMA = 0.9  # 折扣因子
EPSILON = 1e-4  # 收敛阈值
# 终点(3,3)，障碍物(1,1)
GOAL = (3, 3)
OBSTACLE = (1, 1)
# 动作对应的坐标变化
ACTION_DELTA = [(-1, 0), (0, 1), (1, 0), (0, -1)]  # 上、右、下、左# 环境模型构建：初始化状态转移矩阵与奖励函数
def build_model():"""这里直接用状态转移矩阵表示环境了，也可以不用。不过那样得每次重新计算在某一状态下选取动作的下一状态，这种是提前算出来所有的了。下面的R和状态转移矩阵类似也是提前初始化全部每步奖励，（Q-Table是所有步的奖励）后面学习DQN算法或者别的深度强化学习算法时拟合的就是类似这种R，这里算是提前感受一下。"""# P(s,a,s')为状态转移矩阵，用三维矩阵的形式表示# 其值表示即在某一状态选择某一动作会到达哪一状态？P = np.zeros((STATES, ACTIONS, STATES))# R(s,a)为奖励函数奖励函数，生成一个STATES*ACTIONS的二维矩阵# 矩阵元素用-1填充，因为默认每步奖励为-1R = np.full((STATES, ACTIONS), -1.0)  # 默认每步奖励-1# 遍历每一状态for s in range(STATES):x, y = s // GRID_SIZE, s % GRID_SIZEif (x, y) == GOAL:continue  # 终点无动作# 遍历每一状态下的每一动作for a in range(ACTIONS):dx, dy = ACTION_DELTA[a]x_next = x + dxy_next = y + dy# 检查边界if x_next < 0 or x_next >= GRID_SIZE or y_next < 0 or y_next >= GRID_SIZE:x_next, y_next = x, y  # 碰壁保持原位# 障碍物阻挡if (x_next, y_next) == OBSTACLE:x_next, y_next = x, ys_next = x_next * GRID_SIZE + y_next# 更新转移概率P[s, a, s_next] = 1.0  # 确定性转移# 到达终点的奖励为0if (x_next, y_next) == GOAL:R[s, a] = 0.0return P, Rdef value_iteration(P, R, gamma=GAMMA, epsilon=EPSILON):V = np.zeros(STATES)V_history = []  # 记录状态值变化while True:V_prev = V.copy()V_history.append(V_prev)for s in range(STATES):if s == GOAL[0] * GRID_SIZE + GOAL[1]:continue  # 终点状态值固定为0# 贝尔曼最优方程：V(s) = max_a [ R(s,a) + γ * sum(P(s,a,s')*V(s')) ]Q = np.sum(P[s] * (R[s].reshape(-1, 1) + gamma * V), axis=1)V[s] = np.max(Q)if np.max(np.abs(V - V_prev)) < epsilon:break# 提取最优策略policy = np.zeros(STATES, dtype=int)for s in range(STATES):Q = np.sum(P[s] * (R[s].reshape(-1, 1) + gamma * V), axis=1)policy[s] = np.argmax(Q)return V, policy, V_historydef plot_value(V, title):plt.figure(figsize=(8, 6))grid = V.reshape((GRID_SIZE, GRID_SIZE))# 绘制网格和状态值plt.imshow(grid, cmap='viridis', origin='upper')plt.colorbar()plt.title(title)# 标注特殊状态for i in range(GRID_SIZE):for j in range(GRID_SIZE):if (i, j) == GOAL:plt.text(j, i, 'GOAL', ha='center', va='center', color='white')elif (i, j) == OBSTACLE:plt.text(j, i, 'BLOCK', ha='center', va='center', color='white')else:plt.text(j, i, f'{V[i * GRID_SIZE + j]:.1f}', ha='center', va='center', color='white')plt.xticks([])plt.yticks([])plt.show()def plot_policy(policy, title):plt.figure(figsize=(8, 6))action_symbol = ['↑', '→', '↓', '←']for i in range(GRID_SIZE):for j in range(GRID_SIZE):s = i * GRID_SIZE + jif (i, j) in [GOAL, OBSTACLE]:plt.text(j, i, 'GOAL' if (i, j) == GOAL else 'BLOCK', ha='center', va='center')else:plt.text(j, i, action_symbol[policy[s]], ha='center', va='center', fontsize=20)plt.xlim(-0.5, GRID_SIZE - 0.5)plt.ylim(-0.5, GRID_SIZE - 0.5)plt.gca().invert_yaxis()plt.title(title)plt.grid(True)plt.show()if __name__ == '__main__':P, R = build_model()V_vi, policy_vi, V_history = value_iteration(P, R)plot_value(V_vi, "Value Iteration - Optimal State Values")plot_policy(policy_vi, "Value Iteration - Optimal Policy")

运行结果：

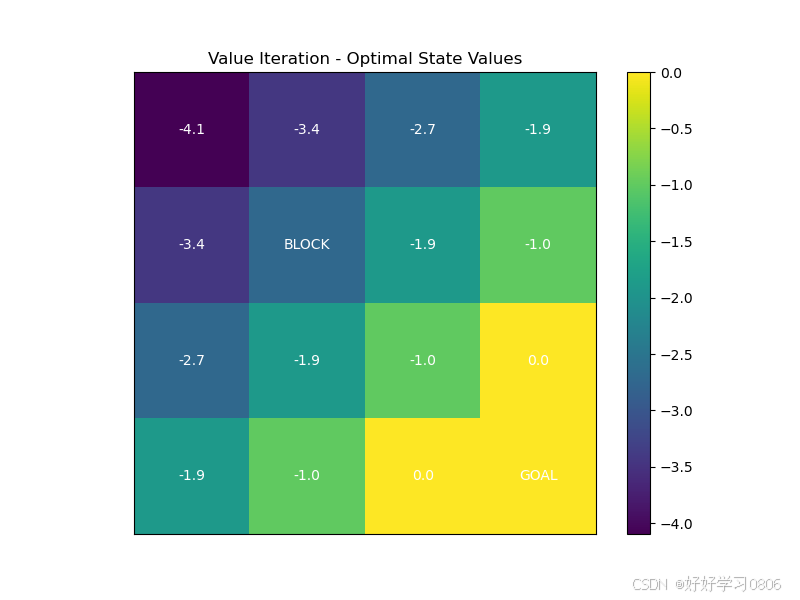
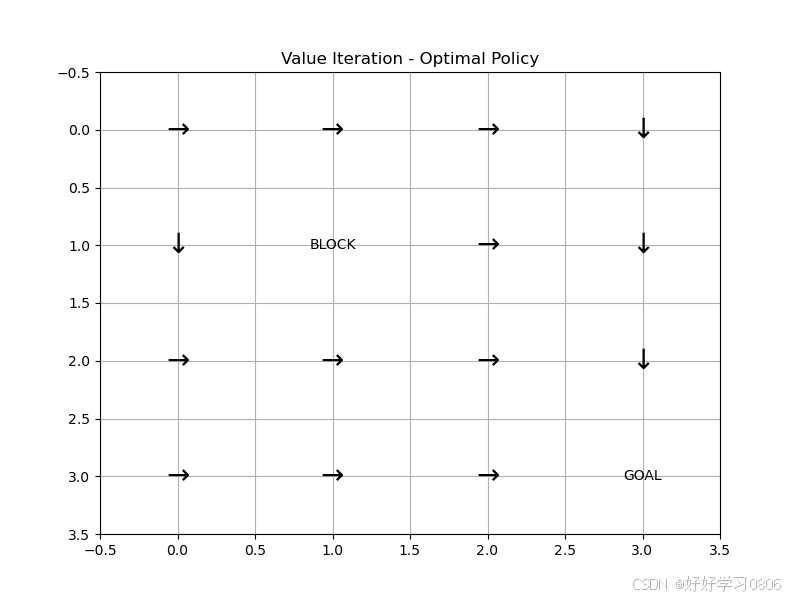
三、总结

从上面的学习，如果仅从算法实现和原理来看，似乎值迭代算法相比策略迭代算法似乎更简单好用？我们可以换个角度来看，会发现策略迭代算法的一些作用是值迭代算法无法完成的。比如收敛速度方面，在面对状态空间较大时的情况，值迭代算法需要更多迭代来调节最优价值，出现“震荡”的情况，而策略迭代每次迭代都能得到一个相对精确的价值函数（但会消耗较多计算资源），再进行修改，其收敛趋势也会更稳定，其收敛轮次也会更少。从算法灵活性来看，策略迭代算法的分步进行的特点具有天然的可改进空间，其灵活性更高。此外，策略迭代每次迭代均能获得一个较为精确的价值，因此，其可解释性也由于值迭代算法。

下表总结了两种算法的特点：

特性	值迭代算法	策略迭代算法
核心思想	直接优化值函数，最后提取策略	交替优化策略和值函数
​更新步骤	每次迭代更新所有状态的值函数	分为策略评估和策略改进两个阶段
收敛性	保证收敛，但迭代次数较多	收敛更快，但单次迭代代价高
是否显式维护策略	否（策略通过值函数隐式提取）	是（显式维护并更新策略）
灵活性	不灵活	灵活
使用场景	状态空间大、动作空间小	状态空间小、策略变化敏感

强化学习算法的系列文章我会在这个月尽量完结，大家可以点点收藏！本人现在只是一名学生，可能有很多理解错误的地方，欢迎大家评论指出，万分感谢！