路径跟踪之导航向量场（三）——无奇异点导航向量场

今天带来导航向量场最后一期文章——无奇异点导航向量场。

1. 引言

还记得我们第一期文章中关于圆的导航向量场介绍吗？导航向量场具有计算量小、实现简单、应用灵活等优点。并且前文所述的导航向量场构建方法通过将期望轨迹转化为隐函数，采用点所在的水平集作为轨迹跟踪误差，成功的避免了在轨迹上寻找最近点的繁琐计算。

不知道大家有没有思考过一个问题，在圆心$(0,0)$处如何计算导航向量场。在圆心$(0,0)$计算梯度$\nabla \varphi$时，其中有部分项分母为0。另外如果是曲线存在自相交的情况，交点处向量场应该如何计算？

在期望轨迹为闭合曲线或有自交点时，必然存在奇异点，也就是导航向量为0的点[1]。尽管有文献可证明这个奇异点集是零测度的[2]，也有很简单的策略能保证无人机掠过奇异点，然而在轨迹更复杂的情况下，这些奇异点仍然是潜在的威胁，可能带来不可预计的后果。本文介绍的文章通过引入参数，将$n$维空间中的期望轨迹映射到$n+1$维的空间中，从而得到一条$n+1$维的无交点非闭合无限曲线，从而避免了奇异点。

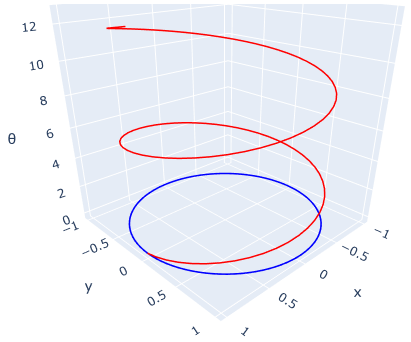
如上图所示，原始期望轨迹为二维空间中的圆（蓝线），通过添加第三轴$\theta$可将其投影为三维空间中的螺旋线（红线），称额外添加的维度$\theta$为虚拟坐标，原始的维度对应的坐标为物理坐标。对红线构建导航向量场，利用导航向量中的物理空间中的项做无人机的实际导引；用虚拟坐标上的项更新无人机的虚拟坐标，实现无奇异点的导航向量场。

2. 期望轨迹构建

一个$n$维空间中的曲线可以写为$n-1$个超曲面的交点。可以直观理解为：一个$n$维空间具有$n$个自由度，而任何一个超曲面（$n-1$维）可约束掉其中一个自由度，因此需要$n-1$个超曲面共同约束，得到仅有1个自由度的$n$维空间中的曲线。因此在二维空间中仅需要一个函数即可定义曲线，而三维空间中需要两个函数。当然，这些超曲面需要有公共交点。下面以三维空间内曲线为例进行说明，感兴趣的读者可根据需求自行推导其他维度。

根据前一篇文章可知，一条三维曲线可表示两个隐函数的零水平集的交线：
P = { x : ϕ i ( x ) = 0 , i = 1 , 2 } \mathcal P = \{\pmb x:\phi_i(\pmb x)=0, i=1,2\} P={xxx:ϕi​(xxx)=0,i=1,2}
其中$x\text{x}x=[x_1,x_2,x_3]$。

现在，我们引入参数$\tau$，将物理空间中的各个维度用参数表示，此时曲线方程变为：
$$\{\begin{array}{r}{x}_1=f_1(\tau )\\ x_2=f_2(\tau )\\ x_3=f_3(\tau )\end{array}$$

令$p\text{p}p=[x_1,x_2,x_3,\tau ]$，${\varphi }_i(p\text{p}p)=x_1-f_i(\tau ),i=1,2,3$，可得升维后的期望轨迹：
P = { p : ϕ i ( p ) = 0 , i = 1 , 2 , 3 } \mathcal P = \{\pmb p:\phi_i(\pmb p)=0, i=1,2,3\} P={p​p​​p:ϕi​(p​p​​p)=0,i=1,2,3}
与三维导航向量场相同，无奇异点导航向量场同样采用$\Phi =[{\varphi }_1,{\varphi }_2,{\varphi }_3]$表示轨迹跟踪误差。

例：假设有一个三维空间中倾斜的圆轨迹，圆心在原点处，所在平面与$XOY$平面夹角$45°$，则其可表示为一个球面和一个平面的交线，也即是：
$$\begin{array}{rl}{\varphi }_1& =x^2+y^2+z^2-r^2=0\\ {\varphi }_2& =x-y=0\end{array}$$
现在引入参数$\tau$分别表示$xyz$，可表示为：
$$\begin{array}{rl}x& =r\frac{\cos \tau }{\sqrt{2}}\\ y& =r\frac{\cos \tau }{\sqrt{2}}\\ z& =r\sin \tau \end{array}$$
因此，该曲线在四维空间下的隐函数表示就可以写作：
$$\begin{array}{rl}{\varphi }_1& =x-r\frac{\cos \tau }{\sqrt{2}}\\ {\varphi }_2& =y-r\frac{\cos \tau }{\sqrt{2}}\\ {\varphi }_3& =z-r\sin \tau \end{array}$$
至此，一个$xyz$三维空间下的曲线就转化到了$xyz\tau$的四维空间下。

3. 无奇异点导航向量场的构建

如前一篇文章所述，导航向量场由收敛项和传播项两项组成：
$$\chi (p\text{p}p)={\chi }_n(p\text{p}p)+{\chi }_t(p\text{p}p)$$
根据前述的期望轨迹形式，计算可得各个超曲面的偏导数$\nabla {\varphi }_i$:
$$\nabla \Phi =\left[\begin{array}{c}\nabla {\varphi }_1\\ \nabla {\varphi }_2\\ \nabla {\varphi }_3\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& -f_1^{\prime }(\tau )\\ 0& 1& 0& -f_2^{\prime }(\tau )\\ 0& 0& 1& -f_3^{\prime }(\tau )\end{array}\right]$$
由此，可计算得到收敛项${\chi }_n$：
$$\begin{array}{rl}{\chi }_n=& -\Phi K\text{K}K\nabla \Phi \\ =& -\sum _{i=1}^3{k}_i{\varphi }_i\nabla {\varphi }_i\\ =& -\left[\begin{array}{cccc}{k}_1{\varphi }_1& k_2{\varphi }_2& k_3{\varphi }_3& -{\sum }_{i=1}^3{k}_i{\varphi }_i{f}_i^{\prime }(\tau )\end{array}\right]\end{array}$$
式中 K = d i a g { k i , k 2 , k 3 } , k i > 0 \pmb K=diag\{k_i,k_2,k_3\},k_i>0 KKK=diag{ki​,k2​,k3​},ki​>0 为收敛项增益矩阵。

同样可以计算得到传播项${\chi }_t$:
$${\chi }_t={\nabla }_{\times }\Phi =\left[\begin{array}{cccc}{f}_1^{\prime }(\tau )& f_2^{\prime }(\tau )& f_3^{\prime }(\tau )& 1\end{array}\right]$$
式中${\nabla }_{\times }\Phi$表示$\nabla \Phi$的楔积。

可证明${\chi }_t$与$\nabla {\varphi }_i$均正交，而${\chi }_n$为$\nabla {\varphi }_i$的线性组合，因此，${\chi }_t$与${\chi }_n$正交。由于${\chi }_n$总是沿着误差$\Phi$的负梯度方向，因此总是倾向于使$||\Phi ||$减小；而传播项${\chi }_t$与误差$\Phi$梯度正交，也就意味着无人机沿着${\chi }_t$运动不会引起误差改变，当误差收敛为$0\text{0}0$时，${\chi }_t$方向即为轨迹切线方向。

由导航向量场的表示形式也可见，由于${\chi }_t$和${\chi }_n$正交，且$||{\chi }_t||$恒大于0，因此$||\chi (p\text{p}p)||>0$，也就意味着这种导航向量场没有奇异点，可实现全局收敛。

4. 数值仿真

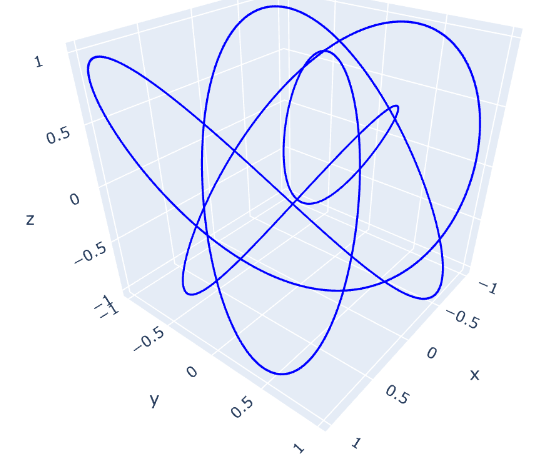
以李萨如曲线为例，定义期望轨迹为：
$$\begin{array}{rl}{x}_1& =f_1(\tau )=\sin (3\tau )\\ x_2& =f_2(\tau )=\sin (4\tau +\pi /4)\\ x_3& =f_3(\tau )=\sin (5\tau +\pi /5)\end{array}$$

1. 写为隐函数形式：
   $$\begin{array}{rl}{\varphi }_1(p\text{p}p)& =x_1-\sin (3\tau )\\ {\varphi }_2(p\text{p}p)& =x_2-\sin (4\tau +\pi /4)\\ {\varphi }_3(p\text{p}p)& =x_3-\sin (5\tau +\pi /5)\end{array}$$
2. 计算超曲面梯度
   根据前文，计算误差梯度有：
   $$\nabla \Phi =\left[\begin{array}{cccc}1& 0& 0& -3\cos (3\tau )\\ 0& 1& 0& -4\cos (4\tau +\pi /4)\\ 0& 0& 1& -5\cos (3\tau +\pi /5)\end{array}\right]$$
3. 计算导航向量场
   取收敛项增益均为$k$，计算其导航向量场有：
   $$\begin{array}{rl}\chi =& {\chi }_t+{\chi }_n\\ =& {\left[\begin{array}{c}3\cos (3\tau )\\ 4\cos (4\tau +\pi /4)\\ 5\cos (5\tau +\pi /5)\\ 1\end{array}\right]}^{\top }+k{\left[\begin{array}{c}\sin (3\tau )-x_1\\ \sin (4\tau +\pi /4)-x_2\\ \sin (5\tau +\pi /5)-x_3\\ {\sum }_{i=1}^3{\varphi }_i{f}_i^{\prime }(\tau )\end{array}\right]}^{\top }\end{array}$$
4. 设置初值进行仿真
   设置初始位置为$p\text{p}p=[x_0,y_0,z_0,{\tau }_0]$，其中$x_0,y_0,z_0$需要根据无人机实际位置给出，${\tau }_0$可任意给定，若能找到更为贴近期望轨迹的${\tau }_0$，可加快收敛过程。本例中给定$p\text{p}p=[0,0,0,0]$（设置速度$v=0.1$，增益$k=5$，仿真飞行$200s$）可得飞行结果如下：
   

5. 总结

本文所介绍的无奇异点导航向量场，在上一篇文章的基础上，通过引入参数将原始轨迹升维，使得原始的$n$维轨迹（不管是闭合的还是有自交点的）在$n+1$维的空间中映射为一条无限不自交的曲线，从而避免了可能存在的奇异点问题；同时由于该方法仍然使用水平集表示轨迹跟踪误差，因此保留了原方法计算量小的特点。

此外，由于此方法采用参数轨迹作为期望轨迹，也就意味着用户可以使用多项式曲线或者B样条曲线等参数曲线作为无人机飞行的期望轨迹，给期望轨迹的设计灵活性带来了极大的提高，使得此方法更具有实用意义。

此处附上我们团队采用多项式轨迹作为期望轨迹、利用三自由度固定翼无人机模型得到的仿真飞行轨迹图。

6. 参考文献

[1] H. Khalil, Nonlinear Systems, 3rd ed. Prentice Hall, 2002.

[2] GONCALVES V M,PIMENTA L C A,MAIA C A,et al. Vector fields for robot navigation along time-varying curves in ndimensions[J]. IEEE Transactions on Robotics,2010,26(4): 647-659

END

后续会陆续带来规划、控制相关的文章、仿真分享。

迅翼SwiftWing致力于固定翼技术共享，汇聚固定翼领域技术极客，推动固定翼技术持续创新！