当前位置：首页 > news >正文

LeetCode从入门到超凡（三）回溯算法

news 2024/9/25 7:12:45

head-bar

引言

大家好，我是GISer Liu😁，一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年9月学习赛的LeetCode学习总结文档；本文主要讲解回溯算法。💕💕😊

介绍

回溯算法（Backtracking） 是一种基于试错思想的搜索算法，旨在通过系统地探索所有可能的解空间来寻找问题的解。它通过逐步构建候选解，并在发现当前路径无法满足求解条件时，回退到上一步（即回溯），重新选择其他可能的路径，从而避免不必要的搜索。这种“走不通就回退”的策略使得回溯算法在处理复杂问题时具有较高的效率。

回溯算法的核心思想可以概括为：

试探与回退：在搜索过程中，算法会尝试每一种可能的选择，如果发现当前选择无法继续构建有效的解，则回退到上一步，尝试其他选择。
递归实现：回溯算法通常通过递归的方式来实现，每一层递归对应于解空间中的一个决策点。

在回溯过程中，可能会出现以下两种情况：

找到解：在尝试过程中，如果找到了一个满足所有条件的解，算法会将其作为最终答案。
无解：如果尝试了所有可能的路径后，仍然无法找到满足条件的解，算法会宣布问题无解。

通过这种逐步试探与回退的机制，回溯算法能够有效地处理那些需要穷举所有可能解的问题，同时避免陷入不必要的搜索路径。

一、理解回溯算法的思想

以求解 $[1, 2, 3]$ 的全排列为例，我们来讲解一下回溯算法的过程。

选择以 $1$ 为开头的全排列。
1. 选择以 $2$ 为中间数字的全排列，则最后数字只能选择 $3$ 。即排列为： $[1, 2, 3]$ 。
2. 撤销选择以 $3$ 为最后数字的全排列，再撤销选择以 $ 2 $ 为中间数字的全排列。然后选择以 $3$ 为中间数字的全排列，则最后数字只能选择 $2$ ，即排列为： $[1, 3, 2]$ 。
撤销选择以 $2$ 为最后数字的全排列，再撤销选择以 $ 3 $ 为中间数字的全排列，再撤销选择以 $1$ 为开头的全排列。然后选择以 $2$ 开头的全排列。
1. 选择以 $1$ 为中间数字的全排列，则最后数字只能选择 $3$ 。即排列为： $[2, 1, 3]$ 。
2. 撤销选择以 $3$ 为最后数字的全排列，再撤销选择以 $1$ 为中间数字的全排列。然后选择以 $3$ 为中间数字的全排列，则最后数字只能选择 $1$ ，即排列为： $[2, 3, 1]$ 。
撤销选择以 $1$ 为最后数字的全排列，再撤销选择以 $3$ 为中间数字的全排列，再撤销选择以 $2$ 为开头的全排列，选择以 $3$ 开头的全排列。
1. 选择以 $1$ 为中间数字的全排列，则最后数字只能选择 $2$ 。即排列为： $[3, 1, 2]$ 。
2. 撤销选择以 $2$ 为最后数字的全排列，再撤销选择以 $1$ 为中间数字的全排列。然后选择以 $2$ 为中间数字的全排列，则最后数字只能选择 $1$ ，即排列为： $[3, 2, 1]$ 。

总结一下全排列的回溯过程：

按顺序枚举每一位上可能出现的数字，之前已经出现的数字在接下来要选择的数字中不能再次出现。
对于每一位，进行如下几步：
1. 选择元素：从可选元素列表中选择一个之前没有出现过的元素。
2. 递归搜索：从选择的元素出发，一层层地递归搜索剩下位数，直到遇到边界条件时，不再向下搜索。
3. 撤销选择：一层层地撤销之前选择的元素，转而进行另一个分支的搜索。直到完全遍历完所有可能的路径。

对于上述决策过程，我们也可以用一棵决策树来表示：

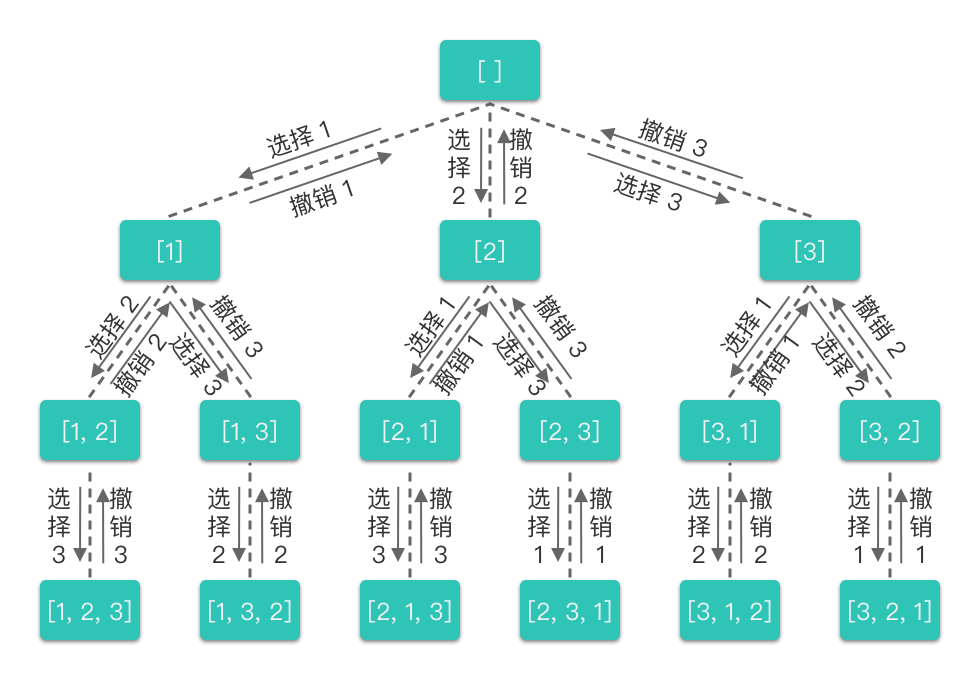
从全排列的决策树中我们可以看出：

每一层中有一个或多个不同的节点，这些节点以及节点所连接的分支代表了「不同的选择」。
每一个节点代表了求解全排列问题的一个「状态」，这些状态是通过「不同的值」来表现的。
每向下递推一层就是在「可选元素列表」中选择一个「元素」加入到「当前状态」。
当一个决策分支探索完成之后，会逐层向上进行回溯。
每向上回溯一层，就是把所选择的「元素」从「当前状态」中移除，回退到没有选择该元素时的状态（或者说重置状态），从而进行其他分支的探索。

根据上文的思路和决策树，我们来写一下全排列的回溯算法代码（假设给定数组 $n u m s$ 中不存在重复元素）。则代码如下所示：

class Solution:def permute(self, nums: List[int]) -> List[List[int]]:res = []    # 存放所有符合条件结果的集合path = []   # 存放当前符合条件的结果def backtracking(nums):             # nums 为选择元素列表if len(path) == len(nums):      # 说明找到了一组符合条件的结果res.append(path[:])         # 将当前符合条件的结果放入集合中returnfor i in range(len(nums)):      # 枚举可选元素列表if nums[i] not in path:     # 从当前路径中没有出现的数字中选择path.append(nums[i])    # 选择元素backtracking(nums)      # 递归搜索path.pop()              # 撤销选择backtracking(nums)return res

根据上文全排列的回溯算法代码，我们可以抽象提炼出回溯算法的通用模板，回溯算法的通用模板代码如下所示：

res = []    # 存放所欲符合条件结果的集合
path = []   # 存放当前符合条件的结果
def backtracking(nums):             # nums 为选择元素列表if 遇到边界条件:                  # 说明找到了一组符合条件的结果res.append(path[:])         # 将当前符合条件的结果放入集合中returnfor i in range(len(nums)):      # 枚举可选元素列表path.append(nums[i])        # 选择元素backtracking(nums)          # 递归搜索path.pop()                  # 撤销选择backtracking(nums)

二、整理解决方案

1.思考

网络教程中的思路如下：

1.根据所给问题，定义问题的解空间：要定义合适的解空间，包括解的组织形式和显约束。

解的组织形式：将解的组织形式都规范为⼀个 $n$ 元组 ${x_1, x_2 …, x_n}$ 。
显约束：对解分量的取值范围的限定，可以控制解空间的大小。

2.确定解空间的组织结构：解空间的组织结构通常以解空间树的方式形象地表达，根据解空间树的不同，解空间分为⼦集树、排列树、 $m$ 叉树等。

3.搜索解空间：按照深度优先搜索策略，根据隐约束（约束函数和限界函数），在解空间中搜索问题的可⾏解或最优解。当发现当前节点不满⾜求解条件时，就回溯，尝试其他路径。

如果问题只是求可⾏解，则只需设定约束函数即可，如果要求最优解，则需要设定约束函数和限界函数。

这种回溯算法的解题步骤太过于抽象，不利于我们在日常做题时进行思考。其实在递归算法知识的相关章节中，我们根据递归的基本思想总结了递归三步走的书写步骤。同样，根据回溯算法的基本思想，我们也来总结一下回溯算法三步走的书写步骤。

回溯算法的基本思想是：以深度优先搜索的方式，根据产生子节点的条件约束，搜索问题的解。当发现当前节点已不满足求解条件时，就「回溯」返回，尝试其他的路径。

那么，在写回溯算法时，我们可以按照这个思想来书写回溯算法，具体步骤如下：

明确所有选择：画出搜索过程的决策树，根据决策树来确定搜索路径。
明确终止条件：推敲出递归的终止条件，以及递归终止时的要执行的处理方法。
将决策树和终止条件翻译成代码：
1. 定义回溯函数（明确函数意义、传入参数、返回结果等）。
2. 书写回溯函数主体（给出约束条件、选择元素、递归搜索、撤销选择部分）。
3. 明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

2.明确所有选择

决策树是帮助我们理清搜索过程的一个很好的工具。我们可以画出搜索过程的决策树，根据决策树来帮助我们确定搜索范围和对应的搜索路径。

3.明确终止条件

回溯算法的终止条件也就是决策树的底层，即达到无法再做选择的条件。

回溯函数的终止条件一般为给定深度、叶子节点、非叶子节点（包括根节点）、所有节点等。并且还要给出在终止条件下的处理方法，比如输出答案，将当前符合条件的结果放入集合中等等。

###4. 将决策树和终止条件翻译成代码
在明确所有选择和明确终止条件之后，我们就可以将其翻译成代码了。这一步也可以分为 $ 3 $ 步来做：

定义回溯函数（明确函数意义、传入参数、返回结果等）。
书写回溯函数主体（给出约束条件、选择元素、递归搜索、撤销选择部分）。
明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

5.定义回溯函数

在定义回溯函数时，一定要明确递归函数的意义，也就是要明白这个问题的传入参数和全局变量是什么，最终返回的结果是要解决的什么问题。

传入参数和全局变量：是由递归搜索阶段时的「当前状态」来决定的。最好是能通过传入参数和全局变量直接记录「当前状态」。

比如全排列中，backtracking(nums) 这个函数的传入参数是 $ nums $（可选择的元素列表），全局变量是 $ res $（存放所有符合条件结果的集合数组）和 $ path $（存放当前符合条件的结果）。$ nums $ 表示当前可选的元素，$ path $ 用于记录递归搜索阶段的「当前状态」。$ res $ 则用来保存递归搜索阶段的「所有状态」。

返回结果：返回结果是在遇到递归终止条件时，需要向上一层函数返回的信息。

一般回溯函数的返回结果都是单个节点或单个数值，告诉上一层函数我们当前的搜索结果是什么即可。

当然，如果使用全局变量来保存「当前状态」的话，也可以不需要向上一层函数返回结果，即返回空结果。比如上文中的全排列。

6.书写回溯函数主体

根据当前可选择的元素列表、给定的约束条件（例如之前已经出现的数字在接下来要选择的数字中不能再次出现）、存放当前状态的变量，我们就可以写出回溯函数的主体部分了。即：

for i in range(len(nums)):          # 枚举可选元素列表if 满足约束条件:                  # 约束条件path.append(nums[i])        # 选择元素backtracking(nums)          # 递归搜索path.pop()                  # 撤销选择

7.明确递归终止条件

这一步其实就是将递归终止条件和终止条件下的处理方法转换为代码中的条件语句和对应的执行语句。

三、回溯算法案例

八皇后问题

51. 八皇后 - 力扣（LeetCode）

1.题意

描述：给定一个整数 $ n = 8 $，返回所有不同的「八皇后问题」的解决方案。每一种解法包含一个不同的棋子放置方案，其中 Q 代表皇后，. 代表空位。

2.说明

八皇后问题：将 8 个皇后放置在 $ 8 \times 8 $ 的棋盘上，使得皇后彼此之间不能攻击。
攻击规则：任何两个皇后不能在同一行、同一列或同一斜线上。

3.示例

示例 1：
- 输入：n = 8
- 输出：[[“.Q…”,“…Q…”,“…Q…”,“…Q.”,“Q…”,“…Q…”,“…Q.”,“…Q…”], […]]
- 解释：八皇后问题存在多个不同的解法。

4. 解题思路

这道题是经典的回溯问题。我们按行顺序放置皇后，从第一行开始逐行放置，直到最后一行。

uml

对于 $\times 8$ 的棋盘，每一行有 8 种放法。我们尝试选择其中一列，检查是否与之前的皇后冲突。如果没有，则继续在下一行放置皇后，直到成功放置所有皇后。之后，我们通过回溯尝试其他可能的分支。

5.回溯步骤

明确所有选择：根据当前行的所有列位置选择放置皇后，形成决策树。
明确终止条件：当遍历到决策树的叶子节点（即最后一行放置完皇后）时，递归终止。
将决策树和终止条件翻译成代码：

def isValid(self, row: int, col: int, chessboard: List[List[str]]):for i in range(row):if chessboard[i][col] == 'Q':return Falsefor i, j in zip(range(row - 1, -1, -1), range(col - 1, -1, -1)):if j >= 0 and chessboard[i][j] == 'Q':return Falsefor i, j in zip(range(row - 1, -1, -1), range(col + 1, 8)):if j < 8 and chessboard[i][j] == 'Q':return Falsereturn Truefor col in range(8):if self.isValid(row, col, chessboard):chessboard[row][col] = 'Q'backtrack(row + 1, chessboard)chessboard[row][col] = '.'

6. 回溯函数定义

使用一个 $\times 8$ 的二维数组 chessboard 表示棋盘状态，初始都为 .。
定义回溯函数 backtrack(chessboard, row)，传入当前棋盘和正在考虑放置的行。全局变量 res 存放所有结果。

res = []
chessboard = [['.' for _ in range(8)] for _ in range(8)]def backtrack(chessboard, row):if row == 8:  # 终止条件res.append([''.join(r) for r in chessboard])return

7. 回溯函数主体

遍历当前行的所有列，判断是否可以放置皇后。如果可以，则放置并递归处理下一行，最后撤销选择。

for col in range(8):if isValid(row, col, chessboard):chessboard[row][col] = 'Q'  # 放置皇后backtrack(chessboard, row + 1)  # 递归处理下一行chessboard[row][col] = '.'  # 撤销选择

8. 递归终止条件

当放置到最后一行时，存储当前棋盘状态到结果数组中。

if row == 8:  # 终止条件res.append([''.join(r) for r in chessboard])return

9.完整解决代码

from typing import Listclass Solution:def __init__(self):self.res = []def solveNQueens(self, n: int) -> List[List[str]]:self.res.clear()chessboard = [['.' for _ in range(n)] for _ in range(n)]self.backtrack(n, 0, chessboard)return self.resdef backtrack(self, n: int, row: int, chessboard: List[List[str]]):# 终止条件：如果放置到最后一行，保存当前解if row == n:temp_res = []for temp in chessboard:temp_str = ''.join(temp)temp_res.append(temp_str)self.res.append(temp_res)returnfor col in range(n):if self.isValid(n, row, col, chessboard):chessboard[row][col] = 'Q'  # 选择位置放置皇后self.backtrack(n, row + 1, chessboard)  # 递归放置下一行chessboard[row][col] = '.'  # 撤销选择，回溯def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]):# 检查列是否有冲突for i in range(row):if chessboard[i][col] == 'Q':return False# 检查左上对角线是否有冲突for i, j in zip(range(row, -1, -1), range(col, -1, -1)):if chessboard[i][j] == 'Q':return False# 检查右上对角线是否有冲突for i, j in zip(range(row, -1, -1), range(col, n)):if chessboard[i][j] == 'Q':return Falsereturn True# 使用示例
if __name__ == "__main__":solution = Solution()results = solution.solveNQueens(8)for res in results:for row in res:print(row)print()

演示代码

1.八皇后问题演示Demo

import matplotlib.pyplot as plt
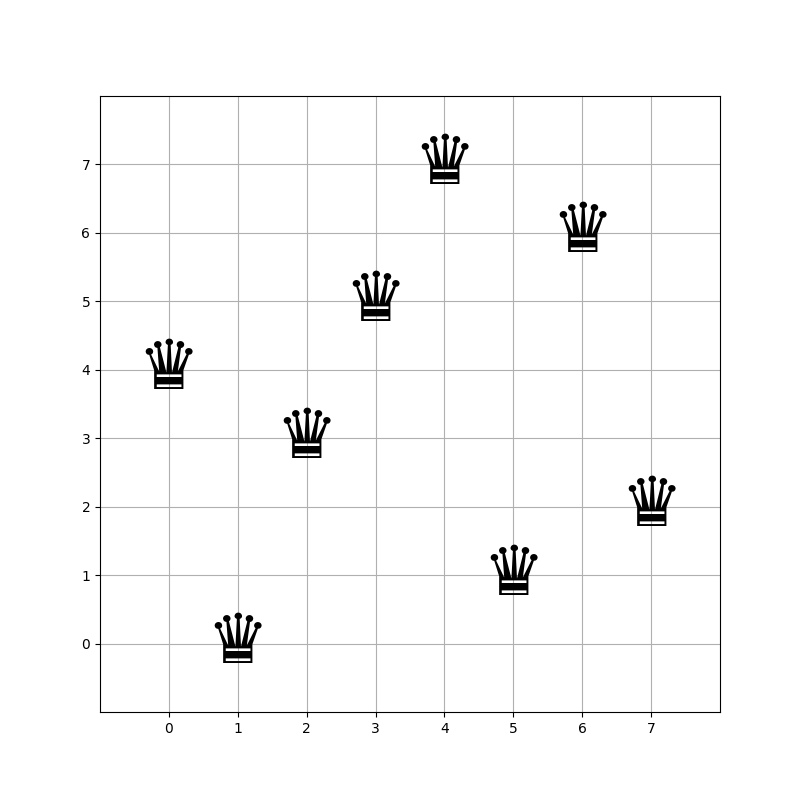
import numpy as npclass NQueens:def __init__(self, n):self.n = nself.solutions = []def is_safe(self, board, row, col):# 检查列是否安全for i in range(row):if board[i] == col or \board[i] - i == col - row or \board[i] + i == col + row:return Falsereturn Truedef solve_n_queens(self, board, row):if row == self.n:self.solutions.append(board.copy())returnfor col in range(self.n):if self.is_safe(board, row, col):board[row] = col  # 放置皇后self.solve_n_queens(board, row + 1)board[row] = -1  # 回溯，撤回皇后def visualize(self):fig, ax = plt.subplots(figsize=(8, 8))for solution in self.solutions:ax.clear()ax.set_xlim(-1, self.n)ax.set_ylim(-1, self.n)ax.set_xticks(range(self.n))ax.set_yticks(range(self.n))ax.grid(True)for r in range(self.n):c = solution[r]ax.text(c, r, '♛', fontsize=50, ha='center', va='center')plt.pause(1)  # 暂停1秒以显示每个解plt.show()if __name__ == "__main__":n = 8  # 皇后的数量board = [-1] * n  # 初始化棋盘queens = NQueens(n)queens.solve_n_queens(board, 0)  # 开始解决问题queens.visualize()  # 可视化解决方案

各位读者可以自行运行测试；如下图所示，感谢GPT-4o的辅助教学😘；

2.排列组合问题演示Demo

代码如下：

import matplotlib.pyplot as plt
import numpy as npclass PermutationTree:def __init__(self):self.fig, self.ax = plt.subplots(figsize=(12, 8))self.results = []self.depth = 0  # 记录当前深度def backtrack(self, path, nums, depth):if len(path) == len(nums):self.results.append(path.copy())self.visualize(path, depth, is_solution=True)returnfor i in range(len(nums)):if nums[i] is not None:  # 确保当前元素未被使用path.append(nums[i])temp = nums[i]nums[i] = None  # 标记为已使用self.visualize(path, depth)self.backtrack(path, nums, depth + 1)nums[i] = temp  # 回溯，恢复状态path.pop()  # 移除最后一个元素def visualize(self, path, depth, is_solution=False):self.ax.clear()self.ax.set_xlim(-1, len(path) + 1)self.ax.set_ylim(-1, depth + 1)self.ax.set_xticks(range(len(path) + 1))self.ax.set_yticks(range(depth + 1))self.ax.grid(True)for i, value in enumerate(path):self.ax.text(i, depth, str(value), fontsize=20, ha='center', va='center')if is_solution:self.ax.text(len(path) // 2, depth + 0.5, "Solution!", fontsize=20, color='green', ha='center')plt.pause(1)  # 暂停1秒以显示当前状态def generate_permutations(self, nums):self.backtrack([], nums, self.depth)plt.show()if __name__ == "__main__":nums = [1, 2, 3]  # 要排列的数字pt = PermutationTree()pt.generate_permutations(nums)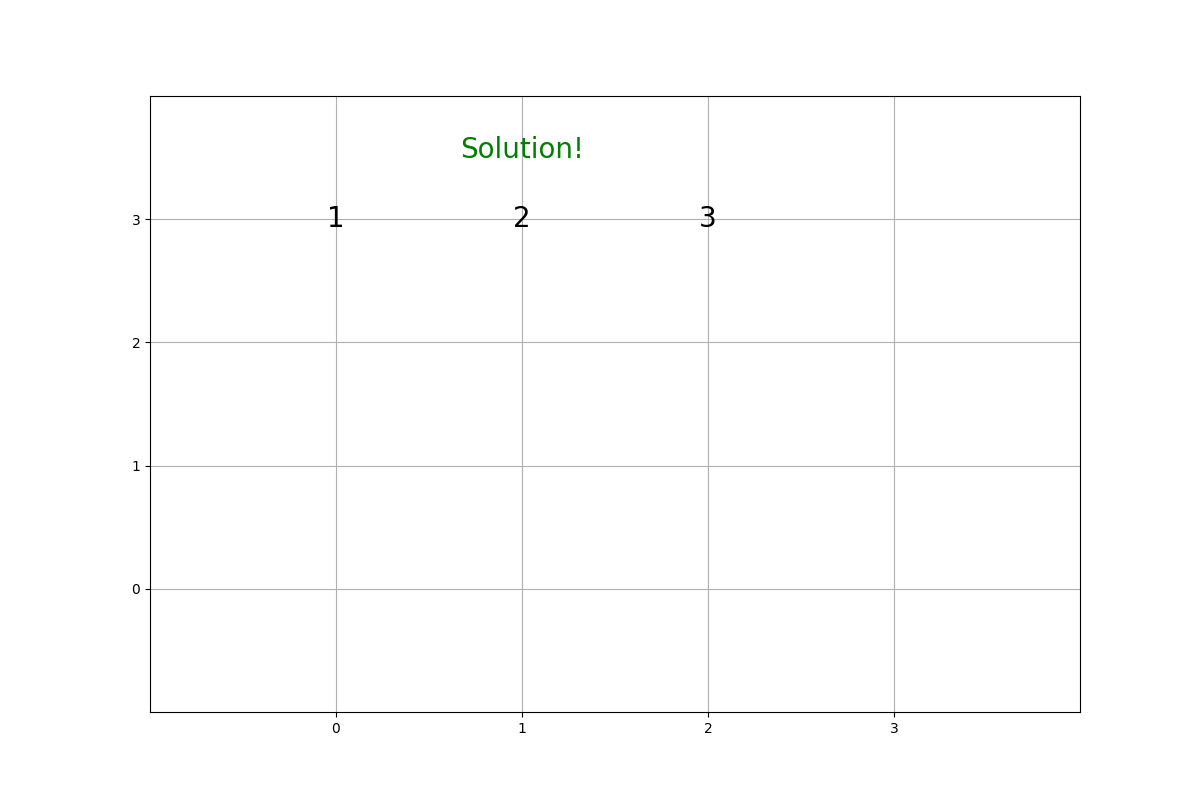

Over!! 今天就学习到这了，各位同好，一起刷题呀😘👌👌