9. 什么是 Beam Search?深入理解模型生成策略
是不是总感觉很熟悉?Beam Search 是生成任务中常用的一种方法。
在之前第5,7,8篇文章中,我们都曾经用到过与它相关的参数,而对于早就有着实操经验的同学们,想必见到的更多。这篇文章将从示例到数学原理和代码带你进行理解。Beam Search 对应的中文翻译为“集束搜索”或“束搜索”。你可以将其当作是贪心算法的拓展,其实是很简单的概念:贪心算法每次只选择最好的,而 Beam Search 会在多个候选中进行选择。通过这篇文章,你将了解到:
- Beam Width(束宽) 的实际作用,常对应于参数名
num_beams。- 所有候选序列生成结束标记 的含义,常对应于参数名
early_stopping。- Beam Search 的基本原理和工作机制。
强烈建议访问:Beam Search Visualizer,这是一个非常 Amazing 的交互式项目,在即将完成这个文章攥写的时候我通过官方文档发现了它,让理论与实际搭上了桥。
notebook 代码下载
文章目录
- Beam Search 的工作原理
- 生成示例
- 怎么处理 `<eos>` ?
- 处理示例图(k=3)
- 进一步深入 Beam Search
- 使用对数概率
- 参数解释
- 代码演示
- 数学描述
- 序列概率
- 评分函数
- Beam Search 的更新步骤
- 最终选择
- 实际应用
- 代码示例
- 对比不同束宽的输出
- 推荐阅读
Beam Search 的工作原理
Beam Search 是一种宽度优先搜索算法,通过保留多个候选序列来探索可能的输出空间,这与贪心算法每次只选择一个当前最优序列不同,可以将贪心算法当成一个候选序列下的 Beam Search。
具体来讲,每一步生成时,Beam Search 会保留束宽 k k k 个最有可能的候选序列(k=1即贪心),并为每个候选序列计算它们的累积概率或对数概率。在每一步搜索时,Beam Search 会生成所有可能的下一个词汇,并从中选择得分最高的 k k k 个序列继续下一步。所以,束宽越大,搜索空间越广,计算成本越高。
以下是 Beam Search 的基本步骤:
- 初始化:从一个初始序列(通常为空或特殊起始标记)开始,设定束宽 k k k,初始化候选序列集 B 0 = { start } B_0 = \{ \text{start} \} B0={start}。
- 迭代生成:对于当前所有候选序列 B t − 1 B_{t-1} Bt−1,扩展一个新的词汇或符号,生成所有可能的下一个词汇组合,并计算每个序列的概率。
- 选择顶束:从所有扩展的候选序列中,选择得分最高的 k k k 个序列,作为下一步的候选序列 B t B_t Bt。
- 终止条件:当所有候选序列都生成了结束标记(如
<eos>)或达到设定的最大长度 T T T 时,停止生成。 - 选择最终序列:从最终的候选序列集中,选择得分最高的序列作为输出。
注:以GPT为例,扩展实际对应于去获取 tokens 的概率。
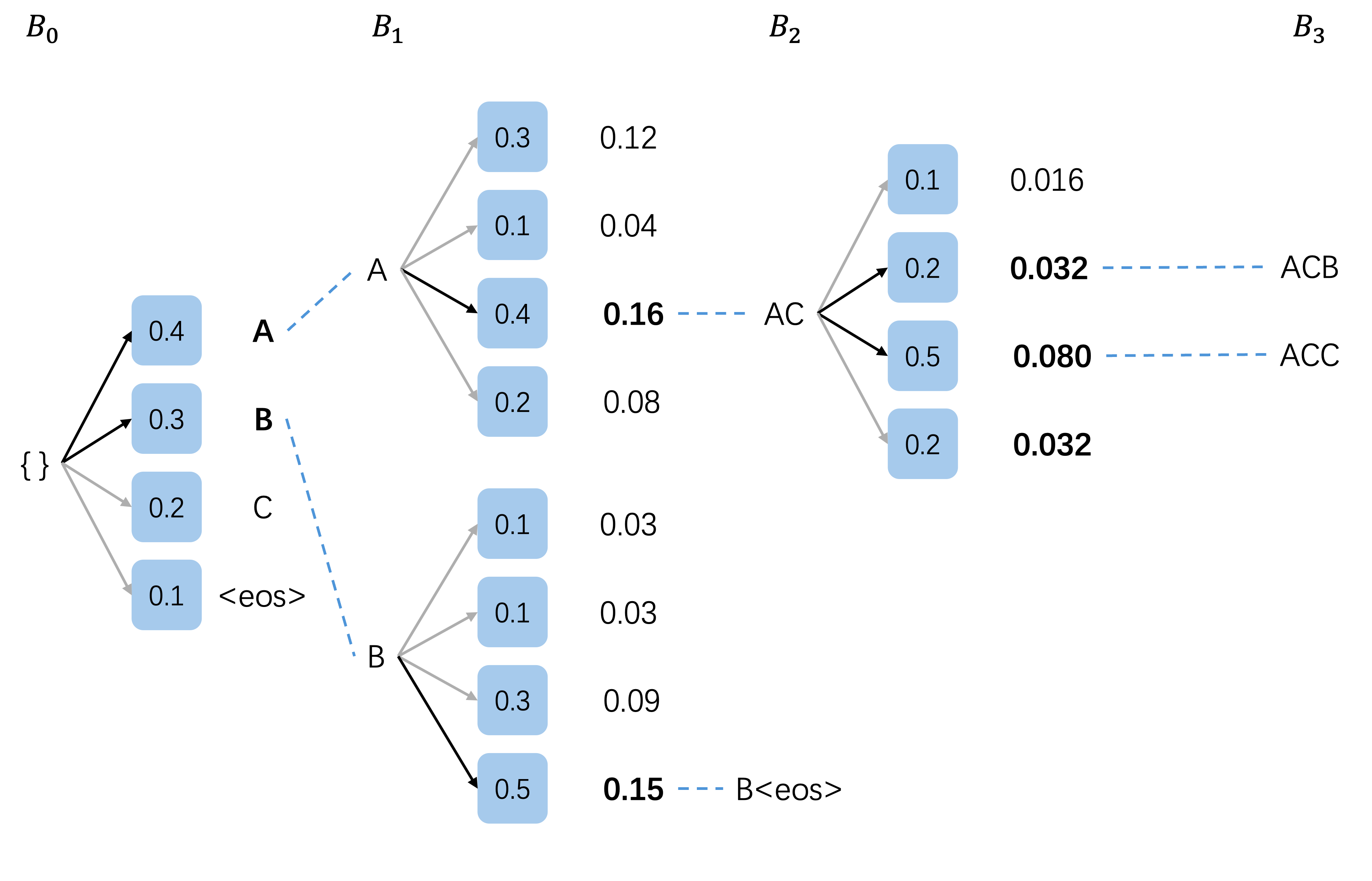
生成示例
为了清晰,这里使用累积概率进行得分的计算。
-
初始化
- 束宽 ( k k k): 2
- 当前候选集 ( B 0 B_0 B0): { (空) } \{\text{(空)}\} {(空)}
- 词汇表 { A , B , C , <eos> } \{A, B, C, \texttt{<eos>}\} {A,B,C,<eos>}
- 扩展(生成所有可能的下一个词汇):
扩展结果 概率 A A A 0.4 \textbf{0.4} 0.4 B B B 0.3 \textbf{0.3} 0.3 C C C 0.2 0.2 0.2 <eos> \texttt{<eos>} <eos> 0.1 0.1 0.1 - 选择顶束 ( k = 2 k=2 k=2):
- A A A ( 0.4 0.4 0.4)
- B B B ( 0.3 0.3 0.3)
- 新的候选集 ( B 1 B_1 B1): { A ( 0.4 ) , B ( 0.3 ) } \{A (0.4), B (0.3)\} {A(0.4),B(0.3)}
-
扩展 A A A 和 B B B
-
扩展 A A A:
- 生成概率: { A : 0.3 , B : 0.1 , C : 0.4 , <eos> : 0.2 } \{A: 0.3, B: 0.1, C: 0.4, \texttt{<eos>}: 0.2\} {A:0.3,B:0.1,C:0.4,<eos>:0.2}
扩展结果 概率计算 概率 A A AA AA 0.4 × 0.3 0.4 \times 0.3 0.4×0.3 0.12 \textbf{0.12} 0.12 A B AB AB 0.4 × 0.1 0.4 \times 0.1 0.4×0.1 0.04 0.04 0.04 A C AC AC 0.4 × 0.4 0.4 \times 0.4 0.4×0.4 0.16 \textbf{0.16} 0.16 A <eos> A\texttt{<eos>} A<eos> 0.4 × 0.2 0.4 \times 0.2 0.4×0.2 0.08 0.08 0.08 -
扩展 B B B:
- 生成概率: { A : 0.1 , B : 0.1 , C : 0.3 , <eos> : 0.5 } \{A: 0.1, B: 0.1, C: 0.3, \texttt{<eos>}: 0.5\} {A:0.1,B:0.1,C:0.3,<eos>:0.5}
扩展结果 概率计算 概率 B A BA BA 0.3 × 0.1 0.3 \times 0.1 0.3×0.1 0.03 0.03 0.03 B B BB BB 0.3 × 0.1 0.3 \times 0.1 0.3×0.1 0.03 0.03 0.03 B C BC BC 0.3 × 0.3 0.3 \times 0.3 0.3×0.3 0.09 \textbf{0.09} 0.09 B <eos> B\texttt{<eos>} B<eos> 0.3 × 0.5 0.3 \times 0.5 0.3×0.5 0.15 \textbf{0.15} 0.15 -
所有扩展序列及其概率:
序列 概率 A C AC AC 0.16 \textbf{0.16} 0.16 A A AA AA 0.12 0.12 0.12 B <eos> B\texttt{<eos>} B<eos> 0.15 \textbf{0.15} 0.15 B C BC BC 0.09 0.09 0.09 A <eos> A\texttt{<eos>} A<eos> 0.08 0.08 0.08 A B AB AB 0.04 0.04 0.04 B A BA BA 0.03 0.03 0.03 B B BB BB 0.03 0.03 0.03 -
选择顶束 ( k = 2 k=2 k=2):
- A C AC AC ( 0.16 0.16 0.16)
- B <eos> B\texttt{<eos>} B<eos> ( 0.15 0.15 0.15)
-
新的候选集 ( B 2 B_2 B2): { A C ( 0.16 ) , B <eos> ( 0.15 ) } \{AC (0.16), B\texttt{<eos>} (0.15)\} {AC(0.16),B<eos>(0.15)}
-
完成集合: B <eos> {B\texttt{<eos>}} B<eos> ( 0.15 0.15 0.15)
-
-
仅扩展 A C AC AC
- 生成概率: { A : 0.1 , B : 0.2 , C : 0.5 , <eos> : 0.2 } \{A: 0.1, B: 0.2, C: 0.5, \texttt{<eos>}: 0.2\} {A:0.1,B:0.2,C:0.5,<eos>:0.2}
扩展结果 概率计算 概率 A C A ACA ACA 0.16 × 0.1 0.16 \times 0.1 0.16×0.1 0.016 0.016 0.016 A C B ACB ACB 0.16 × 0.2 0.16 \times 0.2 0.16×0.2 0.032 \textbf{0.032} 0.032 A C C ACC ACC 0.16 × 0.5 0.16 \times 0.5 0.16×0.5 0.080 \textbf{0.080} 0.080 A C <eos> AC\texttt{<eos>} AC<eos> 0.16 × 0.2 0.16 \times 0.2 0.16×0.2 0.032 \textbf{0.032} 0.032 - 由于 B <eos> B\texttt{<eos>} B<eos> 已完成,我们选择扩展结果中的顶束:
- A C C ACC ACC ( 0.080 0.080 0.080)
- 以某种规则选择 A C B ACB ACB 或 A C <eos> AC\texttt{<eos>} AC<eos> ( 0.032 0.032 0.032)
- 新的候选集 ( B 3 B_3 B3): { A C C ( 0.080 ) , A C B ( 0.032 ) } \{ACC (0.080), ACB (0.032)\} {ACC(0.080),ACB(0.032)}
- 完成集合: B <eos> ( 0.15 ) {B\texttt{<eos>} (0.15)} B<eos>(0.15)
-
后续步骤
- 继续扩展:重复上述过程,直到所有候选序列都生成了
<eos>或达到设定的最大长度。
- 继续扩展:重复上述过程,直到所有候选序列都生成了
现在是你访问它的最好时机:Beam Search Visualizer
怎么处理 <eos> ?
在每一步生成过程中,如果某个序列生成了 <eos>,则将其标记为完成,不再进行扩展。以下是处理 <eos> 的举例:
- 假设在某一步,序列 A C B ACB ACB 扩展出 A C B <eos> ACB\texttt{<eos>} ACB<eos> ( 0.032 × 1 = 0.032 0.032 \times 1 = 0.032 0.032×1=0.032),则:
- A C B <eos> ACB\texttt{<eos>} ACB<eos> 保留在最终候选集,并不再扩展。
- Beam Search 继续扩展其他未完成的序列,直到所有序列完成或达到最大长度。
问题:如果有一个序列被标记为完成(生成了 <eos>),在下一个扩展步骤中,Beam Search 应该扩展多少个候选序列?
答:束宽 ( k k k) 个
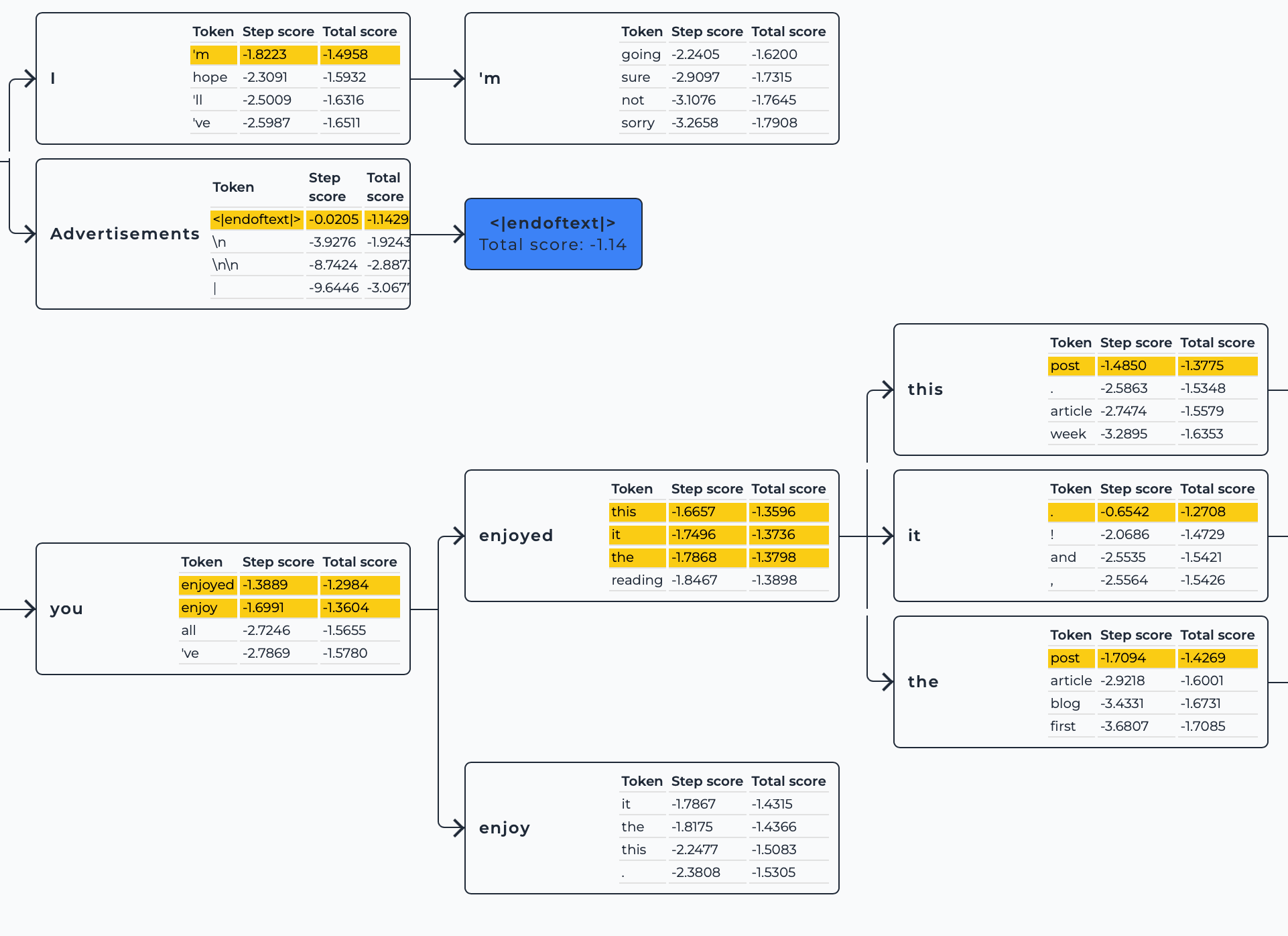
处理示例图(k=3)
你可以在下图中看到,即便有一个序列生成了 <eos>,下一个扩展步骤中还是会扩展 k=3 个候选序列。
进一步深入 Beam Search
使用对数概率
在实际应用中,尤其是在处理长序列时,直接相乘概率会导致数值下溢问题。为了避免这种情况,通常会使用对数概率来累加评分。
示例说明:
假设使用对数概率,序列的评分计算如下:
- 序列 A A A 的概率为 0.4 0.4 0.4,其对数概率为 log ( 0.4 ) ≈ − 0.916 \log(0.4) \approx -0.916 log(0.4)≈−0.916。
- 序列 A C AC AC 的概率为 0.16 0.16 0.16,其对数概率为 log ( 0.16 ) ≈ − 1.833 \log(0.16) \approx -1.833 log(0.16)≈−1.833。
在 Beam Search 中,我们会选择对数概率较高(即绝对值较小)的序列作为顶束。
参数解释
除了 num_beams 和 early_stopping,Beam Search 通常还涉及其他参数,以下是常见参数的简要解释:
max_length(最大生成长度):限制生成序列的最大长度。length_penalty(长度惩罚):用于调整生成序列的长度偏好,通常用于平衡生成序列的长度与概率评分。值大于 1 时,会惩罚过长的序列,值小于 1 时,会鼓励生成较长的序列。no_repeat_ngram_size:防止生成序列中出现重复的 n-gram,提高生成内容的多样性。num_return_sequences:指定生成的序列数量,允许一次生成多个不同的候选序列,<= num_beams。
代码演示
下面是一个 beam search 演示代码,结果完全对应于之前讨论的示例。为了简单起见,我们进一步假设在序列 ACB 和 ACC 之后一定是 <eos>
import mathdef beam_search(initial_sequence, beam_width, max_length, vocab, get_next_probs):beam = [(initial_sequence, 0.0)] # (sequence, log_prob)completed = []for step in range(max_length):print(f"\n第 {step + 1} 步:")all_candidates = []for seq, score in beam:if seq.endswith('<eos>'):completed.append((seq, score))print(f"已完成序列: {seq},得分为 {score}")continuenext_probs = get_next_probs(seq)print(f"扩展序列: {seq},当前得分为 {score}")for token, prob in next_probs.items():new_seq = seq + tokennew_score = score + math.log(prob)all_candidates.append((new_seq, new_score))print(f" 候选序列: {new_seq},得分为 {new_score}")# 对所有候选序列按得分降序排列,选择得分最高的 beam_width 个序列all_candidates.sort(key=lambda x: x[1], reverse=True)beam = all_candidates[:beam_width]# 打印选出的顶束序列print(f"\n选择的 {beam_width} 个顶束序列:")for seq, score in beam:print(f" {seq},得分为 {score}")# 如果没有更多序列可以扩展,则退出循环if not beam:break# 将当前 beam 中剩下的序列加入完成序列中completed += beam# 对完成的序列按得分降序排列,选择得分最高的序列completed.sort(key=lambda x: x[1], reverse=True)print("\n已完成的所有序列:")for seq, score in completed:print(f" {seq},得分为 {score}")return completed[0][0]# 我们之前示例中设置的概率
def get_next_probs(seq):probs = {"": {"A": 0.4, "B": 0.3, "C": 0.2, "<eos>": 0.1},"A": {"A": 0.3, "B": 0.1, "C": 0.4, "<eos>": 0.2},"B": {"A": 0.1, "B": 0.1, "C": 0.3, "<eos>": 0.5},"AC": {"A": 0.1, "B": 0.2, "C": 0.5, "<eos>": 0.2},}return probs.get(seq, {"<eos>": 1.0})initial_sequence = ""
beam_width = 3 # 你可以修改这个参数来感受区别
max_length = 5
vocab = {"A", "B", "C", "<eos>"}best_sequence = beam_search(initial_sequence, beam_width, max_length, vocab, get_next_probs)
print("\n最佳序列:", best_sequence)
输出:
第 1 步:
扩展序列: ,当前得分为 0.0候选序列: A,得分为 -0.916290731874155候选序列: B,得分为 -1.2039728043259361候选序列: C,得分为 -1.6094379124341003候选序列: <eos>,得分为 -2.3025850929940455选择的 2 个顶束序列:A,得分为 -0.916290731874155B,得分为 -1.2039728043259361第 2 步:
扩展序列: A,当前得分为 -0.916290731874155候选序列: AA,得分为 -2.120263536200091候选序列: AB,得分为 -3.2188758248682006候选序列: AC,得分为 -1.83258146374831候选序列: A<eos>,得分为 -2.525728644308255
扩展序列: B,当前得分为 -1.2039728043259361候选序列: BA,得分为 -3.506557897319982候选序列: BB,得分为 -3.506557897319982候选序列: BC,得分为 -2.4079456086518722候选序列: B<eos>,得分为 -1.8971199848858813选择的 2 个顶束序列:AC,得分为 -1.83258146374831B<eos>,得分为 -1.8971199848858813第 3 步:
扩展序列: AC,当前得分为 -1.83258146374831候选序列: ACA,得分为 -4.135166556742355候选序列: ACB,得分为 -3.4420193761824103候选序列: ACC,得分为 -2.525728644308255候选序列: AC<eos>,得分为 -3.4420193761824103
已完成序列: B<eos>,得分为 -1.8971199848858813选择的 2 个顶束序列:ACC,得分为 -2.525728644308255ACB,得分为 -3.4420193761824103第 4 步:
扩展序列: ACC,当前得分为 -2.525728644308255候选序列: ACC<eos>,得分为 -2.525728644308255
扩展序列: ACB,当前得分为 -3.4420193761824103候选序列: ACB<eos>,得分为 -3.4420193761824103选择的 2 个顶束序列:ACC<eos>,得分为 -2.525728644308255ACB<eos>,得分为 -3.4420193761824103第 5 步:
已完成序列: ACC<eos>,得分为 -2.525728644308255
已完成序列: ACB<eos>,得分为 -3.4420193761824103选择的 2 个顶束序列:已完成的所有序列:B<eos>,得分为 -1.8971199848858813ACC<eos>,得分为 -2.525728644308255ACB<eos>,得分为 -3.4420193761824103最佳序列: B<eos>
数学描述
序列概率
假设我们要生成一个长度为 T T T 的序列 Y = ( y 1 , y 2 , … , y T ) Y = (y_1, y_2, \dots, y_T) Y=(y1,y2,…,yT),该序列的生成是逐步进行的,即每个词汇 y t y_t yt 的生成依赖于前面已经生成的词汇 y 1 , y 2 , … , y t − 1 y_1, y_2, \dots, y_{t-1} y1,y2,…,yt−1。因此,序列 Y Y Y 的联合概率为:
P ( Y ) = ∏ t = 1 T P ( y t ∣ y 1 , y 2 , … , y t − 1 ) P(Y) = \prod_{t=1}^{T} P(y_t | y_1, y_2, \dots, y_{t-1}) P(Y)=t=1∏TP(yt∣y1,y2,…,yt−1)
评分函数
由于直接计算概率乘积在处理长序列时容易导致数值下溢问题,通常我们通过取对数来简化计算并稳定数值。取对数后的评分函数(log likelihood)为:
S ( Y ) = log P ( Y ) = ∑ t = 1 T log P ( y t ∣ y 1 , y 2 , … , y t − 1 ) S(Y) = \log P(Y) = \sum_{t=1}^{T} \log P(y_t | y_1, y_2, \dots, y_{t-1}) S(Y)=logP(Y)=t=1∑TlogP(yt∣y1,y2,…,yt−1)
模型的目标是最大化序列的概率:
Y ∗ = arg max Y P ( Y ) Y^* = \arg\max_Y P(Y) Y∗=argYmaxP(Y)
Beam Search 的更新步骤
在每一步 t t t,Beam Search 保留束宽 k k k 个最有可能的部分序列。设候选序列集为 B t − 1 = { Y 1 , Y 2 , … , Y k } B_{t-1} = \{Y_1, Y_2, \dots, Y_k\} Bt−1={Y1,Y2,…,Yk},每个部分序列 Y i Y_i Yi 的概率为 P ( Y i ) P(Y_i) P(Yi)。
- 扩展:对于每个候选序列 Y i ∈ B t − 1 Y_i \in B_{t-1} Yi∈Bt−1,从词汇表 V V V 中扩展所有可能的下一个词汇 y y y,生成新的序列 Y i y Y_i y Yiy(即在 Y i Y_i Yi 的末尾添加词汇 y y y),并计算其概率:
P ( Y i y ) = P ( Y i ) × P ( y ∣ Y i ) P(Y_i y) = P(Y_i) \times P(y | Y_i) P(Yiy)=P(Yi)×P(y∣Yi)
同时取对数后得到评分函数的更新:
S ( Y i y ) = log P ( Y i y ) = S ( Y i ) + log P ( y ∣ Y i ) S(Y_i y) = \log P(Y_i y) = S(Y_i) + \log P(y | Y_i) S(Yiy)=logP(Yiy)=S(Yi)+logP(y∣Yi)
- 选择顶束:在每一步中,我们从所有扩展后的候选序列 { Y i y ∣ Y i ∈ B t − 1 , y ∈ V } \{Y_i y \mid Y_i \in B_{t-1}, y \in V\} {Yiy∣Yi∈Bt−1,y∈V} 中选择得分最高的 k k k 个序列,组成新的候选集 B t B_t Bt:
B t = arg max B ′ ⊆ { Y i y ∣ Y i ∈ B t − 1 , y ∈ V } , ∣ B ′ ∣ = k ∑ Y ′ ∈ B ′ S ( Y ′ ) B_t = \arg\max_{B' \subseteq \{Y_i y \mid Y_i \in B_{t-1}, y \in V\}, |B'| = k} \sum_{Y' \in B'} S(Y') Bt=argB′⊆{Yiy∣Yi∈Bt−1,y∈V},∣B′∣=kmaxY′∈B′∑S(Y′)
最终选择
当生成过程结束时,从最终的候选集 B T B_T BT 中,选择得分最高的序列作为最终输出:
Y ∗ = arg max Y ∈ B T S ( Y ) Y^* = \arg\max_{Y \in B_T} S(Y) Y∗=argY∈BTmaxS(Y)
实际应用
先安装一些演示用到的库:
pip install transformers
pip install torch torchvision torchaudio
代码示例
使用 Hugging Face Transformers 库的简单示例:
import warnings
from transformers import AutoTokenizer, AutoModelForCausalLM
import torch# 忽略 FutureWarning 警告
warnings.filterwarnings("ignore", category=FutureWarning)# 指定模型名称
model_name = "distilgpt2"# 加载分词器和模型
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name)# 移动模型到设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)# 设置模型为评估模式
model.eval()# 输入文本
input_text = "Hello GPT"# 编码输入文本,并生成 attention mask
inputs = tokenizer.encode(input_text, return_tensors="pt").to(device)
attention_mask = torch.ones_like(inputs).to(device)# 生成文本,使用 Beam Search
beam_width = 5
with torch.no_grad():outputs = model.generate(inputs,attention_mask=attention_mask,max_length=50,num_beams=beam_width, # 你可以看到 beam_width 对应的参数名为 num_beamsno_repeat_ngram_size=2,early_stopping=True, # 当所有候选序列生成<eos>停止pad_token_id=tokenizer.eos_token_id)# 解码生成的文本
generated_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("生成的文本:")
print(generated_text)输出:
生成的文本:
Hello GPT.This article was originally published on The Conversation. Read the original article.
对比不同束宽的输出
# 输入文本
input_text = "Hello GPT"# 编码输入文本,同时返回 attention_mask
inputs = tokenizer.encode_plus(input_text, return_tensors="pt", padding=True).to(device)# 设置束宽不同的生成策略
beam_widths = [1, 3, 5] # 使用不同的束宽# 生成并打印结果
for beam_width in beam_widths:with torch.no_grad():outputs = model.generate(inputs["input_ids"],attention_mask=inputs["attention_mask"],max_length=50,num_beams=beam_width,no_repeat_ngram_size=2,early_stopping=True,pad_token_id=tokenizer.eos_token_id)generated_text = tokenizer.decode(outputs[0], skip_special_tokens=True)print(f"束宽 {beam_width} 的生成结果:")print(generated_text)print('-' * 50)束宽 1 的生成结果:
Hello GPT is a free and open source software project that aims to provide a platform for developers to build and use GPGP-based GPSP based GPCs. GPP is an open-source software development platform that is designed to
--------------------------------------------------
束宽 3 的生成结果:
Hello GPT.This article is part of a series of articles on the topic, and will be updated as more information becomes available.
--------------------------------------------------
束宽 5 的生成结果:
Hello GPT.This article was originally published on The Conversation. Read the original article.
--------------------------------------------------
推荐阅读
- Beam-search decoding
- Beam Search Visualizer
