线性回归 (Linear Regression) 多项式回归 (Polynomial Regression)

线性回归 (Linear Regression)

单变量线性回归 (Univariate linear regression)

univariate -> 单变量

代价函数 (Cost function)

代价函数（cost function）：用来衡量假设函数f(x)准确性的工具

线性回归的目标是找到参数w和b，使代价函数J的值最小

$$\{\begin{array}{l}{\hat{y}}^{(i)}=f_{w,b}(x^{(i)})\\ f_{w,b}(x^{(i)})=w{x}^{(i)}+b\end{array}$$

slop: 斜率

**误差 (error): **
$$y-\hat{y}$$
**平方误差 (squared error): **
$$({\hat{y}}^{(i)}-y^{(i)}{)}^2$$

其中 $\hat{y}-y$ 就是误差项（error term），通常记作 ϵ 或 e。

【Squared error cost function】
$$\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$$
m => the number of training examples

Cost function（代价函数）：
$$\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$$
divide by 2 -> 是方便后续计算整洁>

用 $J$ 来表示代价函数：
$$J(w,b)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2$$

回归的目标：通过最小化代价函数 -> 找到最好的参数

$f_w(x)=wx$ 的代价函数

$f_{w,b}(x)=wx+b$ 的代价函数

等高线绘制：椭圆的中心点即为代价函数 $J(w,b)$ 的最小值

梯度下降 (gradient descent) 及公式由来

梯度下降：寻找代价函数的最小值（只能找到局部最低点）

梯度下降公式：

数学基础

导数 偏导数 梯度

导函数 偏导函数 方向导数

偏导 => 相当于求沿着x轴 y轴的导数

例如，求沿 x 轴的偏导，这样平行 x 轴正方向形成一个切面，这时 y 就会成为一个常数，因为切面仅占 y 轴中的一个点。

偏导仅能求平行 x 轴、y 轴的方向的变化趋势

通过叠加 x轴、y轴的方向向量，得到各个方向的变化趋势 => 方向导数

（x、z 轴）

梯度 => 沿着哪个方向走的最快

如果要向其他方向，就需要对两种的数值进行修改，从而才能调整方向，而这种修改都是减小的方式进行的。【类似物理中的两方向不同的力进行叠加】

不损失两边的数值，两边的数值都利用好，对应的方向就是 $(f_z^{\prime }(x_0,y_0),f_x^{\prime }(x_0,y_0))$。

因此就得到了梯度下降的公式【因为两轴方向的数值吃满 因此直接减去偏导】：
$$\{\begin{array}{l}w=w-\alpha \frac{\partial }{\partial w}J(w,b)\\ b=b-\alpha \frac{\partial }{\partial b}J(w,b)\end{array}$$
由梯度公式推导而来，可知两个变量必须同时变化。

α：学习率，即往下走的步子大小

（α不能过大也不能过小，要合理选择）

求偏导易得以下结果：

$$J(w,b)=\frac{1}{2m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$$

$$\begin{array}{rl}\frac{\partial J(w,b)}{\partial w}& =\frac{1}{m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}\\ \frac{\partial J(w,b)}{\partial b}& =\frac{1}{m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)})\end{array}$$

梯度下降的变体

• 批量梯度下降(BGD)：每次迭代计算梯度时使用全部训练样本（严格对应代价函数的定义）
• 随机梯度下降(SGD)：每次随机使用1个样本计算梯度近似
• 小批量梯度下降(MBGD)：每次使用一个小样本子集（如32/64个样本）

计算效率的权衡：

• BGD：梯度方向准确但计算慢
• SGD：计算快但噪声大
• MBGD：平衡两者

在机器学习和优化算法的上下文中，噪声（Noise）指的是梯度估计或优化过程中的随机波动或不准确性。它通常是由于使用数据的子集（而非全体数据）来计算梯度而引入的。

噪声的来源

• 随机梯度下降（SGD）：每次迭代仅用1个随机样本计算梯度，该样本的梯度可能与全体数据的真实梯度方向差异很大，这种偏差就是噪声。
• 小批量梯度下降（MBGD）：用一个小批量（如32个样本）计算梯度，虽然比SGD更稳定，但仍会引入噪声（因为不是全体数据）。
• 批量梯度下降（BGD）：理论上无噪声（用全体数据计算梯度），但计算成本高。

批量梯度下降：每一步下降都使用训练集中的所有样本数据进行计算 （就是上述推导采用的）

Quiz

多类特征 (Multiple features)

多类特征：x 为多个特征组成的向量

${\vec{x}}^{(i)}$ 上的向量符号是可选的，不是必须采用的。

多元线性回归 (Multiple linear regression)

向量化 (Vectorization)

通过向量化，可以较为简洁表达公式，同时编程中也可以提高执行性能。

编写向量化代码，充分利用线性代数及GPU硬件。

原理：多线并行计算，比for循坏快很多

* 和 dot 对比

运算类型	是否默认并行	说明
np.dot(A, B)	✅ 是	调用 BLAS 库（如 OpenBLAS/MKL），支持多线程
A * B（逐元素乘）	❌ 否	通常单线程，但可能用 SIMD 向量化加速

原因

• * 是 逐元素运算，计算模式简单，并行开销可能超过收益。
• np.dot 是 矩阵乘法，计算密集，BLAS 库会主动优化并行。

np.dot 为什么比 Python 循环快？

对比项	np.dot（C + BLAS）	Python 循环
执行方式	编译后的机器码	解释执行（逐行翻译）
内存访问	连续内存优化（SIMD）	无优化，缓存效率低
并行计算	多线程 + SIMD 指令	单线程
底层优化	调用 BLAS（如 MKL、OpenBLAS）	无优化

正常发行版的NumPy貌似不能使用GPU，PyTorch可以，或CuPy

然而NumPy在小规模的时候用的不是多线程，大规模才会使用

向量化通过并行运算极大提升了效率，类似于一种空间换时间的 trade off，同时也表明了向量化的高效主要体现于大数据集的机器学习。

向量化表示多元线性回归的梯度下降：

正规方程 (Normal equation)

• Only for linear regression
• Solve for w, b without iterations

Disadvantages:

• Doesn’t generalize to other learning algorithms. (如逻辑回归算法、神经网络其他算法等)
• Slow when number of features is large (> 10,000)

实际工业场景中，机器学习从业者几乎不会手动实现正规方程（Normal Equation），而是直接调用优化过的库函数（如 scikit-learn、statsmodels 或数值计算库）。

正规方程 vs 梯度下降

1. 正规方程（解析解）

• 定义：
  直接通过数学公式求解线性回归的最优参数 $(w,b)$：
  $$\mathbf{w}=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$

• 适用场景：

  • 小规模数据（特征数 $n<10^4$）。
  • 机器学习库中的实现（如 scikit-learn 的 LinearRegression）。

• 优点：

  • 无需迭代，直接得出解析解。
  • 无需调整超参数（如学习率）。

• 缺点：

  • 计算复杂度高 $O(n^3)$，不适用于高维数据。
  • 若 ${\mathbf{X}}^T\mathbf{X}$ 不可逆（如特征共线性），需使用伪逆或正则化。

2. 梯度下降（迭代优化）

• 定义：
  通过迭代调整参数 $(w,b)$，逐步最小化损失函数（如均方误差）。
• 适用场景：
  • 大规模数据（特征数或样本量极大）。
  • 深度学习和其他复杂模型（如神经网络）。
• 优点：
  • 计算效率高（支持分批计算，如随机梯度下降）。
  • 可扩展至非线性模型。
• 缺点：
  • 需选择学习率等超参数。
  • 可能收敛到局部最优（凸问题如线性回归无此问题）。

实际应用建议

1. 优先调库：
   • 使用 scikit-learn 的 LinearRegression（内部基于正规方程或SVD）。
   • 大规模数据用 SGDRegressor（梯度下降实现）。
2. 手动实现的场景：
   • 教学/面试时理解原理。
   • 定制化需求（如添加特殊约束）。
3. 数值稳定性：
   • 若手动实现，用 np.linalg.pinv 替代逆矩阵计算。

特征缩放

问题的发现

contour plot 等高线图

$x_1$、$x_2$ 取值大小相差较大，导致等高线图中 $w_1$、$w_2$ 取值在两轴上，一侧数值较大，一侧数值较少。

如上图中 $w_2$ 需要变动很大才能保持“等高”，而 $w_1$ 仅需要一点变动数值就可以了。

同一个学习率对于不同的特征不一定都适合，比如 $w_1$ 的取值很小，学习率一定时梯度变换的幅度就会很大，就会来回跳，而 $w_2$ 变换幅度较小，正常逼近。

当不用的特征值取值范围差异很大时，可能导致梯度下降非常缓慢。但是经过重新缩放不同的特征使它们都在相似的范围内取值，这样可以显著加快梯度下降的速度。

如图中通过重新缩放的 $x_1$、$x_2$，等高线会更接近于一个圆形。

实现特征缩放

进行特征缩放的根本原因是学习率对每个特征都是固定的。

除以最大值

均值归一化 (Mean normalization)

$$x_i=\frac{x_i-{\mu }_i}{max-min}$$

将平均值去当作原点，$x_i$ 减去平均值 ${\mu }_i$ 可以当作数值在原点附近的分布位置。在上图 $x_1$ 的范围 $2000-300$ 可以看作是 $x_1$ 的变化幅度，将原点附近的数值除以他的变化幅度来实现它的归一化。

标准差标准化 / Z-score归一化 (Z-score normalization)

概率统计中，正态分布的标准化将参数为 $(\mu ,{\sigma }^2)$ 的正态分布化为参数为 $(0,1)$ 的标准正态分布。

经验定律 (a rule of thumb)

不需要严格徘徊在 [-1, 1] 之间

当然 ，数据归一化并不是万能的。在实际应用中，通过梯度下降法求解的模型通常是需要归一化的包括线性回归、逻辑回归、支持向量机、 神经网络等模型，但对于决策树模型则并不适用。

检查梯度下降是否收敛

单词解释

converge 收敛

如果 $J$ 的值在一次迭代后增加，通常意味着学习率α选择不当即学习率过大，或者代码中有bug。

收敛的判断

• 通过学习曲线判断

• 通过自动收敛测试

自动收敛需要寻找合适的阈值 $\epsilon$ ，这点相当困难。

选择学习率

选择合适学习率非常重要，学习率过小会导致梯度下降速度太慢，学习率过大会甚至导致不会收敛。

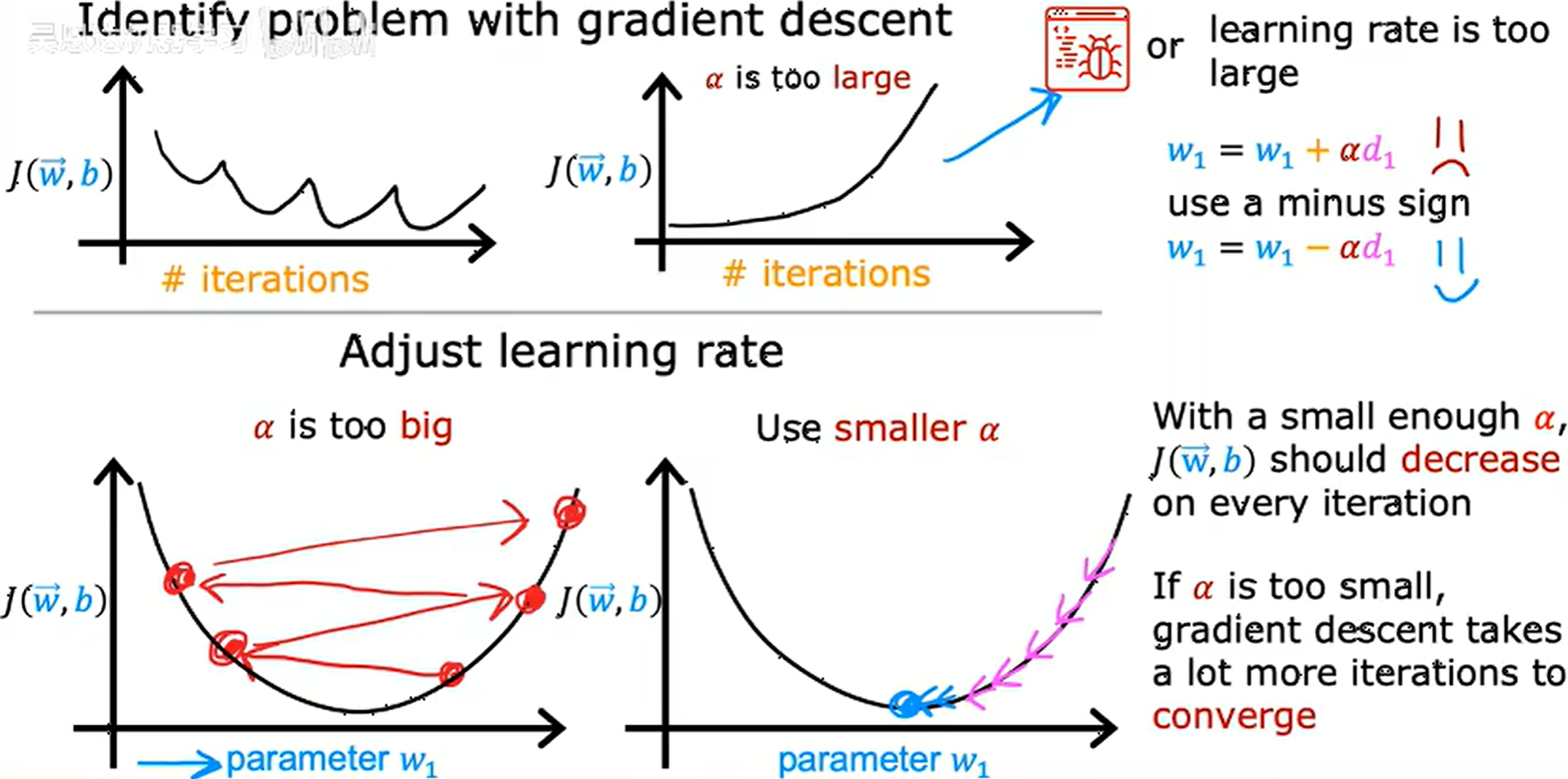
常将学习率设置很小，用来调试代码是否正确。

反复调试来选择到一个合适的学习率

特征工程 (Feature engineering)

特征选择对学习算法的性能有巨大的影响

多项式回归 (Polynomial Regression)

通过将多元线性回归与特征工程结合，通过构造多项式特征来扩展线性模型的能力，从而形成多项式回归（Polynomial Regression）。这是一种经典且强大的方法，可以拟合非线性关系。

在出现平方、立方后，对特征进行缩放尤为的重要。