DX12 快速教程(3) —— 画矩形
快速导航
- 新建项目 "003-DrawRectangle"
- 初识渲染管线
- 什么是渲染管线
- 可编程渲染管线与着色器
- 渲染管线阶段组成
- Input Assembler (IA) Stage 输入装配阶段
- Vertex Shader (VS) Stage 顶点着色器阶段
- 什么是齐次坐标
- 透视与齐次坐标
- 六大坐标空间
- 顶点着色器的目标
- Rasterization (RS) Stage 光栅化阶段
- 裁剪与透视除法
- 视口变换(屏幕映射)
- 背面剔除
- 三角形遍历
- 顶点插值
- Pixel Shader (PS) Stage 像素着色器阶段
- Output Merger (OM) Stage 输出合并阶段
- 开始画三角形吧
新建项目 “003-DrawRectangle”

本文全程高能!渲染管线是重中之重!
初识渲染管线
什么是渲染管线
渲染 (Render),就是将虚拟的三维场景或模型转化为二维图像的过程。

渲染是一个非常复杂的过程,它需要从一系列的顶点、纹理等信息出发,把这些信息最终转换成屏幕图像。

早期的 GPU 仅仅是一个图形加速设备,3D 渲染大头还在 CPU 上,GPU 仅仅是辅助 CPU 加速渲染的。但 CPU 是一个一个串行渲染 3D 物体的,这导致渲染效率极低。
试想一下,如果现在仍然是用 CPU 进行硬渲染,面对 3D 游戏中成千上万的三角面,如果仅仅是逐一单个处理计算,损失的效率是极其惊人的。

随着硬件的升级,GPU 逐步和 CPU 分家,成为一个独立设备登上了历史舞台,人们逐渐认识到渲染任务要从 CPU 转移到 GPU 上。为了高效率渲染,人们把渲染过程自上而下拆分为多个阶段,利用 GPU 多核并行计算 的特点,使每个阶段都能并行执行,这样就能快起来了。


渲染管线 (Rendering Pipeline),就是将上述所有的渲染阶段整合的概念模型。因为这个模型很像工厂里的流水线,每个阶段均可以并行执行,所以得名“管线 (流水线)”。
这可以类比汽车工业的发展,在1913年前福特开发出汽车流水线前,汽车组装只能让一位位工人逐工序完成,年产不过12台,效率极低;而引入了流水线概念后,每位工人只需要做不停地做同一道工序,所有工序并行进行,极大地提高了工厂的生产效率,生产效率提高了8倍。

可编程渲染管线与着色器
固定渲染管线 (Fixed-Function Pipeline) 是一种早期的图形渲染模型,曾在 OpenGL 和 DirectX 等图形API中占据核心地位。它提供了一套固定的功能模块,包括顶点处理、光照计算、纹理映射等,开发者通过调用特定的API接口进行配置,但无法修改这些功能的具体实现。
在 DirectX 8.0 发布之前,渲染管线的表现形式都是固定管线。固定渲染管线的好处是方便,坏处是很不灵活,渲染效果差,无法实现现代多样的渲染效果。

不可灵活定制的固定渲染管线已经被时代抛弃了。 设计者将固定管线中的某些渲染阶段单独抽出来,做成相对独立的可编程 GPU 程序,这些程序就叫 Shader 着色器。


着色器位于 GPU 端,和 CPU 端不同,写着色器是要用到专门的语言的。写着色器用的语言就叫 Shader Language 着色器语言,常见的着色器语言有 DirectX 的 HLSL、OpenGL 和 Vulkan 的 GLSL、Metal 的 MLSL 等。 DX12 要用到 HLSL,我们后面会涉及到 HLSL 的简单编程。

2000年9月,随着 DirectX 8.0 的发布,Shader Model 着色器模型开始流行,图形渲染发生了一场轰轰烈烈的革新,固定管线退出了历史舞台,取而代之的是带着色器、可自定义配置的可编程渲染管线 (Scriptable Render Pipeline)。 现代的渲染管线,基本上都是可编程渲染管线,都要和着色器打交道。

渲染管线阶段组成

Input Assembler (IA) Stage 输入装配阶段

三维模型本质是成千上万的顶点数据,比如一个正方体就有8个顶点,输入装配阶段则是对于模型顶点的第一次处理,获取从 CPU 端输入的顶点数据,并将顶点装配成图元 (Primitive)。

图元就是图形的基本元素。可以是一个点,一条线,或者一个三角形面等等。我们最常用的就是三角形面。

我们在3D软件中做出的各种飞机坦克小姐姐都是由这种基本元素构成。反过来也是一样,我们可以利用图元组合出各种我们想要的图形。

此阶段属于固定阶段,不可编程,只可配置。
Vertex Shader (VS) Stage 顶点着色器阶段

问题来了,屏幕呈现的是二维图像,但我们输入的数据都是三维场景数据啊!如何将一个三维场景,通过适当的变换,变成一个有立体感的二维图像呢?换句话说,如何将一个三维场景变换到适合二维呈现的空间上呢?

Vertex Shader 顶点着色器就是做这个的。这个阶段的任务是:将上一阶段 (Input Assembler 输入装配阶段) 得到的顶点数据,变换到适合二维呈现的 Homogeneous Clipping Space 齐次裁剪空间 里面,为下一阶段的处理做准备。


齐次是啥?裁剪空间又是啥?齐次裁剪空间又是什么鸟东西?别急,我们一个一个解释。
什么是齐次坐标
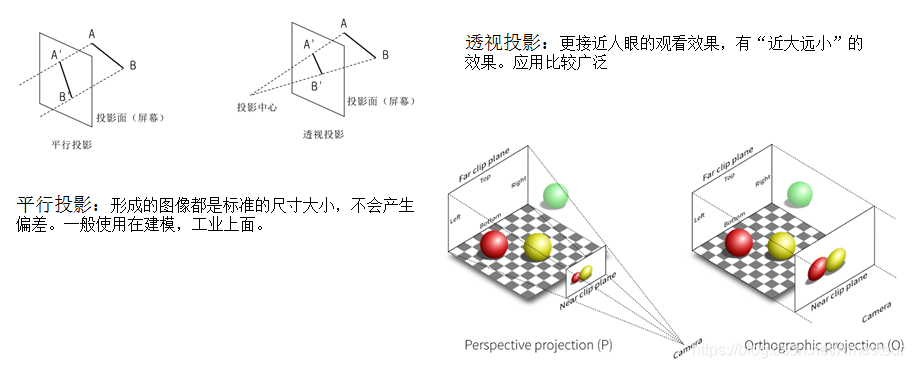
我们先来讨论一下 Projection 投影:
想象投影仪在一个屏幕上投影一张2D图片,很容易就可以得到投影图片的 X, Y 分量。

现在,我们要在投影仪和屏幕之间添加一个 W 分量。W 分量是投影仪到屏幕的距离。

那么 W 分量的作用是什么呢?想象一下,如果我们移动投影仪的位置,来增加或减少 W分量的值,那么投影出的2D图片会发生什么?如果将投影仪靠近屏幕,W分量减小,2D图片缩小;如果投影仪远离屏幕,W分量增大,2D图片放大。

没错,W分量能同时控制 X,Y 分量的大小,进而改变二维图像的大小,这就是 W 分量的作用。
在原有的坐标上加一个维度 W,带 W 分量的坐标,我们称为 Homogeneous Coordinates 齐次坐标。
而这个 W 分量,我们称为 Homogeneous Component 齐次分量。
这个齐次坐标在图形学相当有用,随处可见。

透视与齐次坐标
在欧氏(几何)空间,同一平面的两条平行线永远不能相交,这是我们都熟悉的一种场景。

然而,在生活中,我们的眼睛却可以看到两条平行线相交。例如:火车轨道随着我们的视线越来越窄,最后两条平行线在无穷远处交于一点。

在镜头中,如果猫离相机足够近,远处的大山会比猫看上去小。

上述现象都叫 Perspective 透视 现象,透视遵循 “近大远小” 的原则。

比如上面两张图,左图是相机完全平行于桌面得到的;右图是将手机抬起一定角度后拍摄的。
在两张照片中过Q点添加了一条水平红线,然后将BC分为了绿,蓝两部分。很明显可以看到通过透视投影后,Q点的水平位置不再处于BC中点。
因此,透视实际上是一种近大远小的视觉现象,而右图中DC边离我们近,AB边离我们远,所以造成了正方形的上半部分会被缩放得更加厉害!
我们之前所接触到的三维空间都叫 Euclidean Space 欧几里得空间 (欧氏空间),我们现实所处在的三维立体空间就是欧氏空间。

欧氏空间能很好地描述我们的2D/3D几何空间,但我们的眼睛看到的其实是 Perspective Space 投影空间。欧氏空间不足以处理投影空间,不能很好的解释并处理上面的透视现象。

如果这个点远去到无穷远呢?无穷远处的点在欧氏空间中无法具体展示。在投影空间中,平行线会在无穷远处相遇,但在欧氏空间中却做不到。
如何才能完美解决这个问题?这就要齐次坐标大显身手了!
首先,如果我们要表示一个无穷远的点,我们可以把 W 分量设置为 0:

如果我们要表示一个看得见的点,我们可以把 W 分量设置为 1:

透视常常涉及到 透视投影变换,变换后 W 分量通常都不为 1。W 分量决定了图像的大小,我们可以通过除以 W 分量,拉伸放缩图像。使图像恢复正常大小,符合透视 “近大远小” 的特征。

除以 W 分量的过程,叫做 Perspective Division 透视除法 (也叫齐次除法),进行透视除法的目的,是将 W 分量规范化,得到物体正确的投影大小。
六大坐标空间

- Model Space 模型空间

模型空间 (局部空间),其实是以模型自身中心为坐标原点的三维空间。
- World Space 世界空间

世界空间,其实是以场景中心为坐标原点的三维空间。
我们将一个模型创造好以后,我们一般都需要将它放置到一个和其他的模型在一起的一个地方,组成一个场景,使之更有意义,而这个地方就是“世界空间”。
在这个过程中,我们一般会对某个单独的模型物体进行平移、旋转、缩放等操作,这样模型就能从模型空间变换到世界空间了。
- View Space 观察空间


我们为什么能看到东西呢?答案:我们的眼睛。
在计算机图形学,像眼睛,相机这样能观察模型的东西,统称 Camera 摄像机。
因为模型是以我们的角度去观察的,所以摄像机中心为坐标原点的三维空间叫观察空间。
将世界空间变换到观察空间,实质上是将摄像机和整个世界做整体的旋转和平移,把摄像机弄到世界空间中心上。


- Homogeneous Clip Space 齐次裁剪空间
前置知识:在图形学中,将三维物体和场景降维变换到二维图像的过程称为 Projection 投影。
投影分为两种:Orthographic Projection 正交投影 和 Perspective Projection 透视投影

人眼视野范围其实近似于一个圆台。人眼将三维模型和场景通过投影变成我们所看到的二维图像,于是就产生了透视现象,导致我们看东西近大远小。
但电脑屏幕可是一个方方正正的矩形 (曲面屏除外),怎么才能像人眼一样,将三维物体投影到二维上呢?
为了解决这个问题,人们用棱台代替圆台模拟人的视野范围,这个棱台就叫 View Frustum 视锥体,它是一个透视模型。
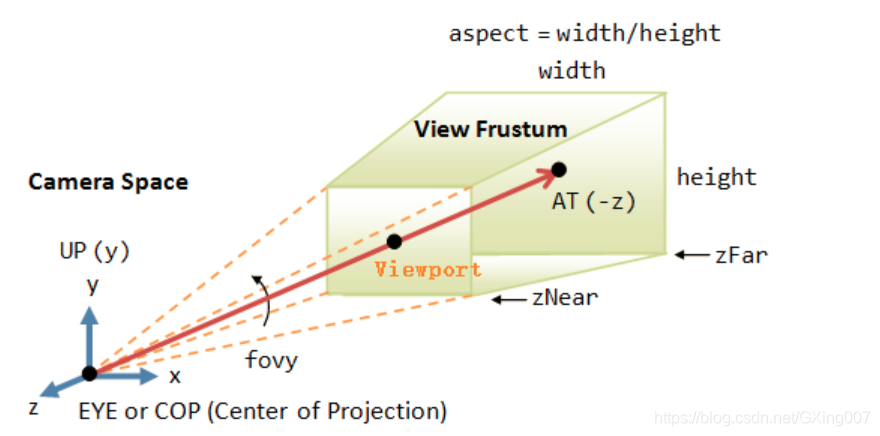

利用视锥体,电脑就可以模拟人眼的透视投影了。

但是问题又来了,棱台上下底面大小是不等的。上底面较小,物体离摄像机越近越大,越靠近上底面,因此上底面又称为 Near Clip Plane 近裁剪面;下底面较大,物体离摄像机越远越小,越靠近下底面,因此下底面又称为 Far Clip Plane 远裁剪面。

但我们的屏幕最多只能表示一个方方正正的棱柱:

似乎视锥体模型不起作用了,屏幕表示不出来,怎么办?
解决方法:透视投影变换,将视锥体棱台"压缩"成棱柱。


经过透视投影变换后的三维空间也改变了,我们把这个空间叫 齐次裁剪空间 (投影空间)。
为什么要叫 “齐次裁剪空间”?因为这个空间其实是要为后面的 裁剪 和 透视除法 (齐次除法) 做准备的,变换到齐次裁剪空间的过程并不是真正的投影,只是将物体由视锥体映射到棱柱上。真正的投影在后面的透视除法。

- Normalized Device Coordinates 标准化设备空间 (NDC 空间)
上文我们提到:经过透视投影变换后,顶点的 W 坐标就不是 1 了!这表明顶点的投影坐标并不正确!我们需要规范化坐标,对顶点坐标做一次透视除法,让坐标都除以 W 分量,使 W 分量为 1,这样才能得到物体正确的投影坐标,这个时候才是对物体真正的投影。

没错,我们做透视除法的时候,又变换了一次空间,这个空间叫 NDC空间。
NDC空间是一个长宽高取值范围为 [-1,1] 的立方体,它的出现是为了统一坐标系,实现屏幕坐标的转换和硬件无关,方便后续我们将坐标映射到屏幕上。
NDC空间可以屏蔽各种尺寸屏幕的差异,使得在投射到屏幕之前的所有处理都无需考虑屏幕尺寸。
- Screen Space 屏幕空间
NDC 空间长宽的范围均是 [-1,1],我们还需要把它拉伸到我们屏幕的尺寸,这样屏幕才能正常呈现图像。最终呈现的三维空间叫 屏幕空间。

顶点着色器的目标
此阶段完全可以编程。
Rasterization (RS) Stage 光栅化阶段
裁剪与透视除法
视口变换(屏幕映射)
背面剔除
三角形遍历
顶点插值
此阶段属于固定阶段,不可编程,只可配置。
Pixel Shader (PS) Stage 像素着色器阶段
此阶段完全可以编程。
Output Merger (OM) Stage 输出合并阶段
此阶段属于固定阶段,不可编程,只可配置。