当前位置：首页 > news >正文

ML 系列：第 23 节 — 离散概率分布（多项式分布）

news 2024/11/23 16:33:16

目录

一、说明

二、多项式分布公式

2.1 多项式分布的解释

2.2 示例

2.3 特殊情况：二项分布

2.4 期望值（Mean）

2.5 方差

三、总结

3.1 python示例

一、说明

伯努利分布对这样一种情况进行建模：随机变量可以采用两个可能的值（通常为 0 和 1）之一，表示二进制结果。此分发适用于单个试用版。当此二元实验重复 n 次时，得到的分布称为二项分布。

以类似的方式，Multinoulli 分布（或分类分布）将概念扩展到单个试验的 k 种可能结果。当具有 k 个结果的实验重复 n 次时，我们得到多项式分布。因此，多项分布描述了 n 次独立试验的结果，每项试验都遵循 Multinoulli 分布。

二、多项式分布公式

多项式分布的概率质量函数由下式给出：

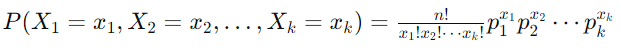
哪里：

2.1 多项式分布的解释

Number of Trials (n): This represents the total number of experiments or trials conducted.
Possible Outcomes (k): Each trial can result in one of k possible outcomes. For example, if you roll a die, there are 6 possible outcomes (1 through 6).
Outcome Counts (𝑥𝑖): These are the counts of each outcome over the 𝑛n trials. For example, if you roll a die 10 times and get three 1’s, two 2’s, one 3, zero 4’s, three 5’s, and one 6, then 𝑥1=3, 𝑥2=2, 𝑥3=1, 𝑥4=0, 𝑥5=3, and 𝑥6=1.
Outcome Probabilities (pi): These are the probabilities of each outcome occurring in a single trial. For a fair die, 𝑝1 = 𝑝2 = 𝑝3 = 𝑝4 = 𝑝5 = 𝑝6 = 1/6
Factorial Terms:

𝑛!(n factorial) is the product of all positive integers up to n.
xi! (x_i factorial) is the product of all positive integers up to xi.

6. Probability Calculation:

2.2 示例

假设你进行了一个将一个公平的6面模具滚动10次的实验，你想找到这种情况下的概率：

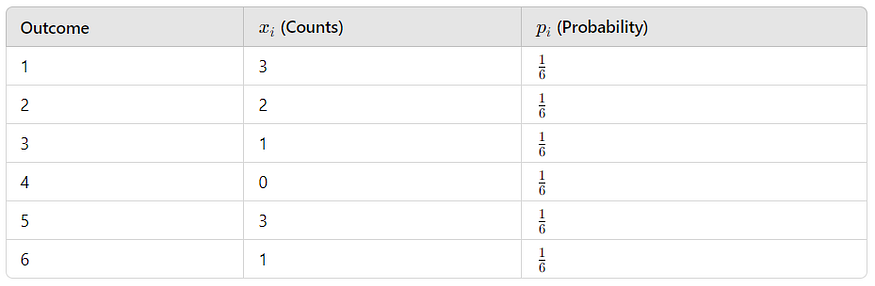
此表指的是获得三个1、两个2、一个3、零4、三个5和一个6。在这里：

n = 10
k = 6
x1 = 3， x2 = 2， x3 = 1， x4 = 0， x5 = 3， x6 = 1
p1 = p2 = p3 = p4 = p5 = p6 = 1/6

将这些代入公式中：

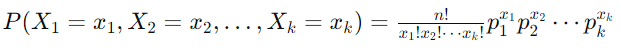
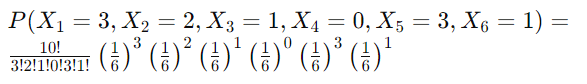
简化此操作可得到：

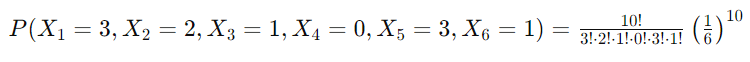
计算阶乘和最终概率：

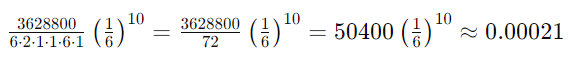
因此，这个特定结果的概率约为 0.00021

2.3 特殊情况：二项分布

当 k = 2 时，多项式分布简化为二项式分布。让我们看看它是如何工作的：

对于 k = 2：

x1 = x 和 x2 = n−x
p1 = p 和 p2 = 1−p

多项式公式变为：

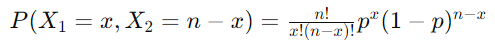
这正是二项分布公式：

2.4 期望值（Mean）

多项式分布中每个随机变量习的期望值 E[习] 由下式给出：

这意味着结果 i 出现的预期次数是试验总数 n 和结果 i pi 的概率的乘积。

2.5 方差

多项式分布中每个随机变量习的方差 Var（习） 由下式给出：

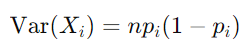
该公式表示结果 i 在其平均值附近出现的次数的可变性或分布。

三、总结

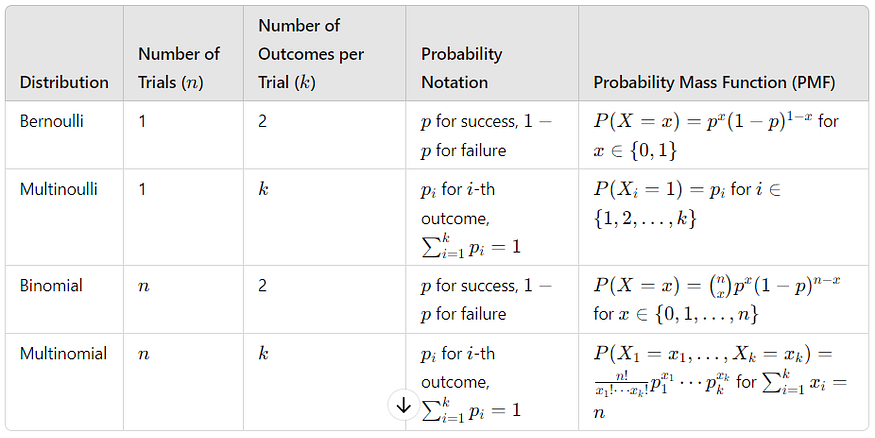
下面是一个汇总表，它根据参数 k 和 n 比较了伯努利分布、多重分布、二项式分布和多项式分布：

3.1 python示例

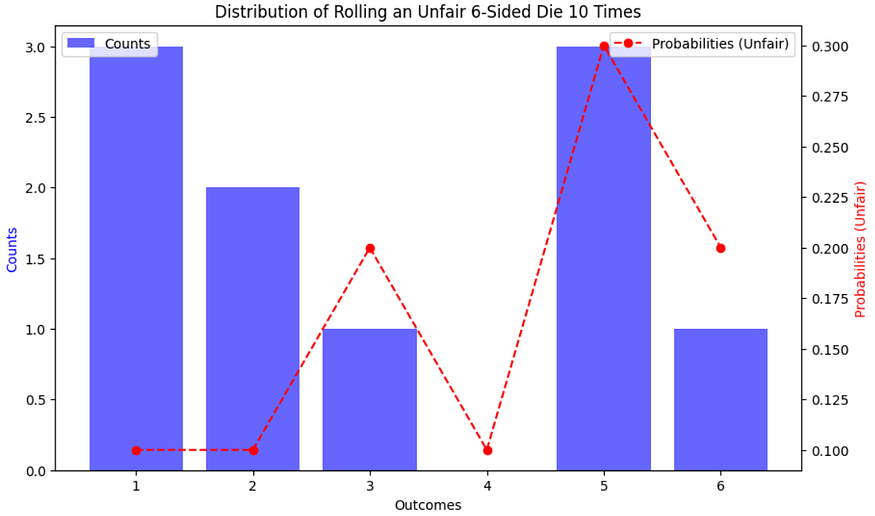
绘制给定实验的分布图（将不公平的 6 面骰子掷 10 次并观察结果的具体计数）：

import matplotlib.pyplot as plt# Data
n = 10
outcomes = [1, 2, 3, 4, 5, 6]
counts = [3, 2, 1, 0, 3, 1]# Define probabilities for an unfair dice
probabilities_unfair = [0.1, 0.1, 0.2, 0.1, 0.3, 0.2]  # Plotting
fig, ax1 = plt.subplots(figsize=(10, 6))# Bar plot for counts
ax1.bar(outcomes, counts, color='b', alpha=0.6, label='Counts')
ax1.set_xlabel('Outcomes')
ax1.set_ylabel('Counts', color='b')
ax1.set_xticks(outcomes)
ax1.set_title(f'Distribution of Rolling an Unfair 6-Sided Die {n} Times')# Line plot for probabilities (unfair)
ax2 = ax1.twinx()
ax2.plot(outcomes, probabilities_unfair, color='r', marker='o', linestyle='dashed', label='Probabilities (Unfair)')
ax2.set_ylabel('Probabilities (Unfair)', color='r')# Adding legends
ax1.legend(loc='upper left')
ax2.legend(loc='upper right')plt.show()

这是代码的输出：