HashMap(深入源码追踪)
一篇让你搞懂HashMap的几个最重要的知识点,往源码跟踪可以让我们很轻松应对所谓的一些八股面试题.
一. 属性解释
先来解释HashMap中重要的常量属性值
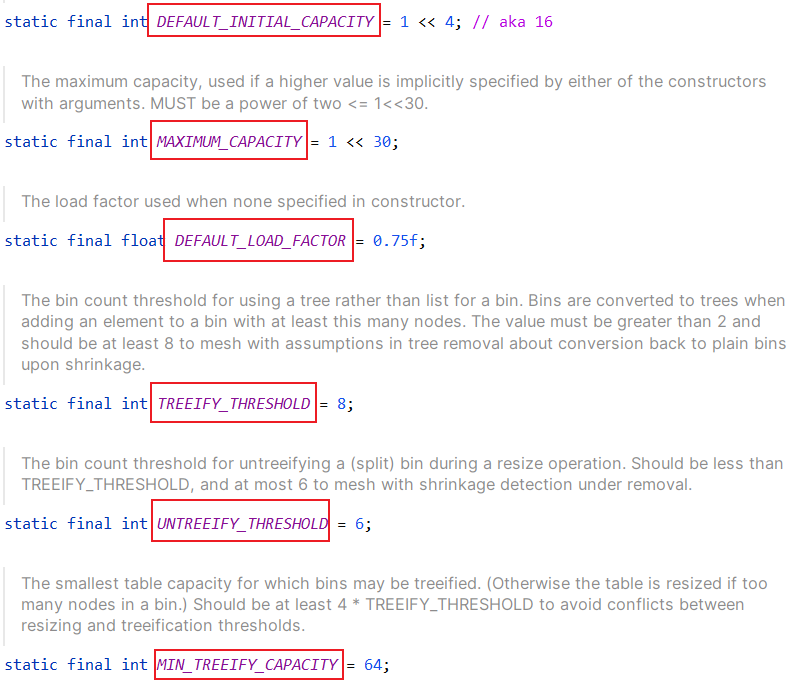
- DEFAULT_INITIAL_CAPACITY : 默认初始化容量,也就是如果不指定初始化的Map存储容量大小,默认生成一个存储16个空间的Map集合
- MAXIMUM_CAPACITY : 最大容量,也就是Map中最多存储 (1 << 30)个节点
- DEFAULT_LOAD_FACTOR: 加载因子,默认为0.75.加载因子的作用就是用来计算HashMap中存储多少节点时需要进行扩容操作.
- TREEIFY_THRESHOLD: 树化阈值.也就是当链表长度大于等于8时,链表可能进行树化操作(这里还需要满足一个Map容量大于等于64条件才可以进行树化).
- UNTREEIFY_THRESHOLD: 非树化阈值,当链表节点小于等于6时,树化结构将会退化为链表结构.
- MIN_TREEIFY_CAPACITY: 最小树化容量,也就是当即满足链表长度大于等于8,又满足此时Map容量为大于等于64时,链表将会进行树化操作.
借用这些属性,我们先来简单看一下,我们在New一个HashMap的时候,会发生什么事情
1.1 构造函数
调用无参构造时

我们发现HashMap并没有去做初始化的操作,仅仅只是把加载因子赋值了默认的加载因子值(0.75f)
HashMap还提供了其他几个构造方法,我们先来看看我们如果指定初始容量的构造函数

继续跟进
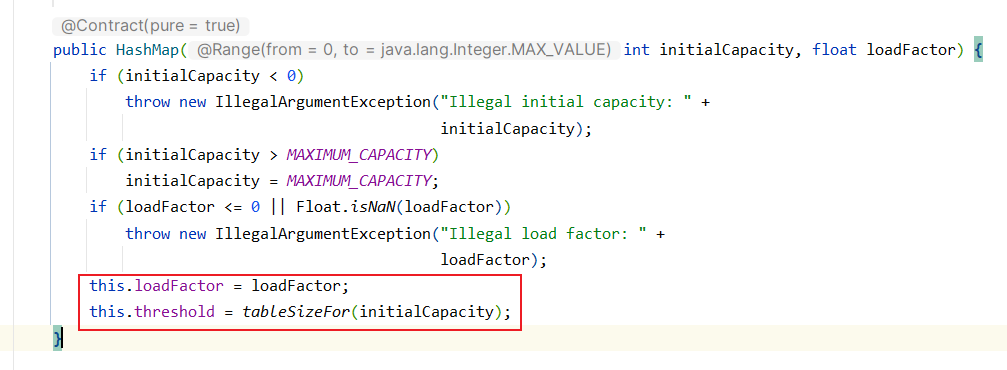
我们发现仅仅也就是给加载因子赋值为默认加载因子值(0.75f),这里还赋值了一个threshold.这是个什么东西?
我们再去查看一下HashMap其他属于每一个HashMap对象的属性值
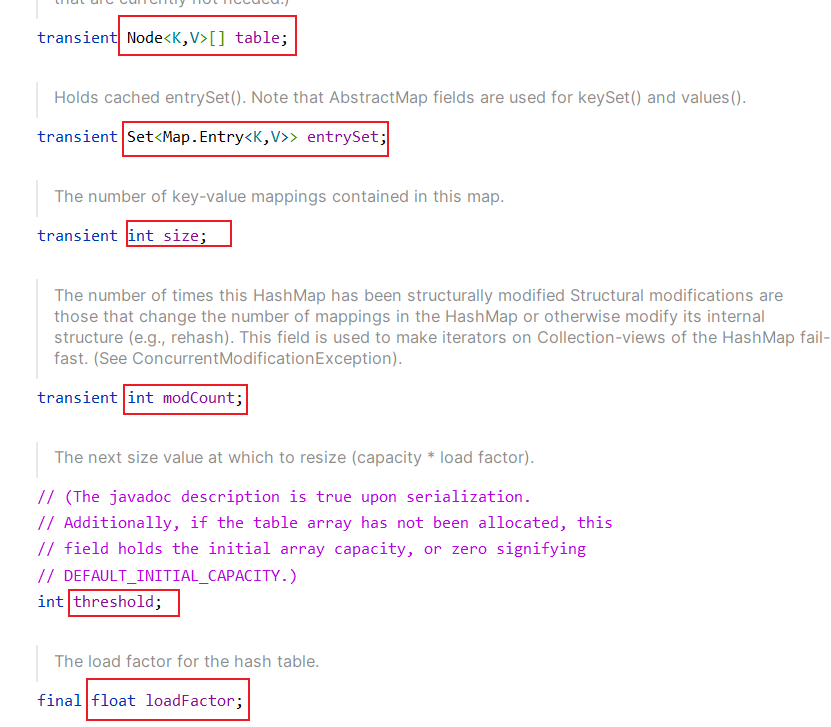
- table : 表,实际上就是哈希表,用来存储我们放的元素的存储结构.存放的是一个Node节点.
- entrySet: 含义是键值对,可以理解为我们将一个Map的映射当成了一个对象.也就是(k,v)当成一个整体
- size: 存放元素的数量.
- modCount: 这个是用来帮助检测集合在迭代过程中是否被修改.为设计快速失败的实现。这意味着如果在创建迭代器之后,集合被以任何方式修改(除了通过迭代器自身的
remove方法),迭代器将抛出 ConcurrentModificationException - threshold: 阈值.这个属性其实有两种代表意思,在中间状态时表示的时数组最大能发多少元素,随后又表明为扩容时机,数组存储多少元素时将进行扩容.
- loadFactor: 加载因子,也就是用来计算阈值的一个乘积因子.
我们再回到之前那个式子,说明此时仅仅只是调整Map能够存储的最大容量.

我们查看一下tableSizeFor这个方法

这里做了两个事情,第一步算出( 当前容量 - 1 )后的前导零的数目,假设就是16,此时算出其减一后的前导0就是28, -1无符号右移28位也就是得到n = 15. 然后判断此时n是否小于0,小于则为1,不小于再判断是否大于设置的最大容量,如果是则调整为最大容量,不是就+1.其实也就是在做一个存放节点数量的适配,限制数组的大小.
二. 存储
在刚刚的叙述中,我们发现了,当我们调用HashMap的构造函数中,并没有去完成table的初始化.仅仅只是对加载因子与阈值做了相应的赋值操作.
如果此时不进行初始化,那么基本只有一种可能,就是我们在存放元素的过程中,将他给初始化了.
我们来查看一下HashMap的put方法

2.1 扰动函数
键的hash方法调用运算,也叫扰动函数.

通过调用hashCode的方法计算key的哈希值,并通过与 哈希值无符号右移16位进行异或运算得到最后的哈希值.也就是将计算的哈希值高位与低位充分组合,使低位也受到高位的影响.这样的设计增加了哈希值的随机性,降低了哈希冲突的概率。异或操作使得低位的特征影响到高位, 减少了相同低位的哈希值导致相同索引位置的情况。
2.1.1 那这里可以提出一个疑问,为什么这样就可以减少哈希冲突呢?
哈希冲突(Hash Collision): 是指在哈希表中,两个不同的输入(即键)经过哈希函数计算后得到了相同的哈希值(即哈希码或哈希地址),从而导致这两个输入被映射到哈希表的同一个槽位(或称为桶)上.
只要哈希函数映射的比较均匀,一般来讲是很难出现哈希碰撞的.
Java当中key的hashCode计算,返回的是一个int型的散列值.那么int值的范围会是-2147483648~2147483647.
加起来也就是需要40亿的一个映射的空间.如果我们使用一个40亿的数组来存放哈希值映射的值,内存是放不下的.所以只可能缩小数组的空间,那缩小,冲突的概率就会提高.那在这样一个前提下,我们想去使数据均匀分布,设计扰动函数是很关键的一步.

注意: 这里讨论的是尽量避免哈希冲突,也就是更希望他能够均匀的落在数组上,而不是我们后面的处理方式能通过链表来解决.
假设HashMap的数组初始容量为16, 就需要用之前哈希函数计算的哈希值对数组的长度进行取模运算来获取余数得到访问数组的下标.
而源码当中实际上是将( 数组长度- 1) 然后与哈希值做 与运算 ,计算机里 位运算比取余 % 运 算要快

这里其实也正好解释了,为什么HashMap的数组长度要取2的整数幂. 因为这样(数组长度 - 1)正好相当于一个 “低位掩码”.与 操作的结果就是散列值的高位 全部归零,只保留低位值,用来做数组下标访问。以初始长度 16 为例,16-1=15。2 进制表示是0000 1111 。和某个散列值做 与 操作如下,结果就是截取了最低的四位值。
这样是要会快捷一些,但是新的问题来了,就算散列值分布再松散,要是只取最后几位的话,碰撞也会很严重。
此时扰动函数的作用就出来啦右移16 位,正好是32位的一半,自己的高半区和低半区做异或,就是为了混合原始哈希码的高位和低位,以此来加大低位的随机性。而且混合后的低位掺杂了高位的部分特征,这样高位的信息也被变相保留下来。
2.2 初始化
我们继续往下看,查看putVal方法
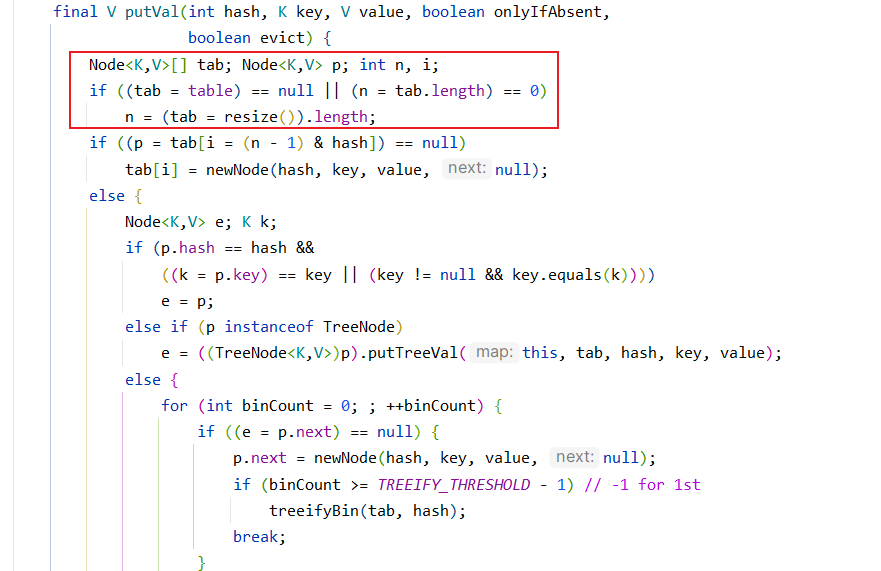
这里解释一个参数:
boolean onlyIfAbsent: 一个布尔值,指示如果键已经存在,是否应该更新其值。如果为true,则仅当键不存在时才插入键值对;如果为false,则无论键是否存在,都更新其值。
我们发现定义一个tab,并将hashmap的成员变量table赋值于它,而我们也清楚此时table应该还未初始化,为null值,我们也可以debug查看.
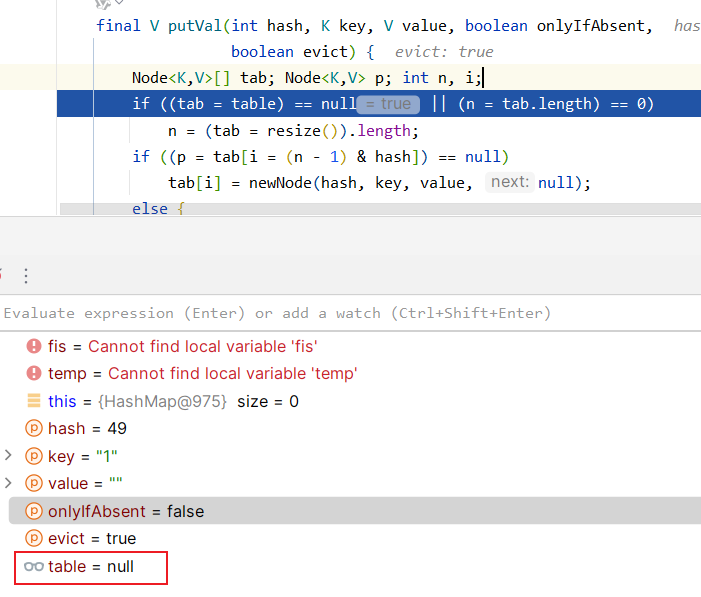
所以接下来将会进入resize()方法.
2.2.1 扩容方法 resize()
resize方法其实就是扩容方法.这里分为三个阶段
- 已经经历初始化的哈希表
- 调用了赋值初始容量的构造函数
- 无参构造
我们这里先来查看无参构造时的扩容初始化(实际上第2个与第三个是一致的,代码流程只有可能执行一次).
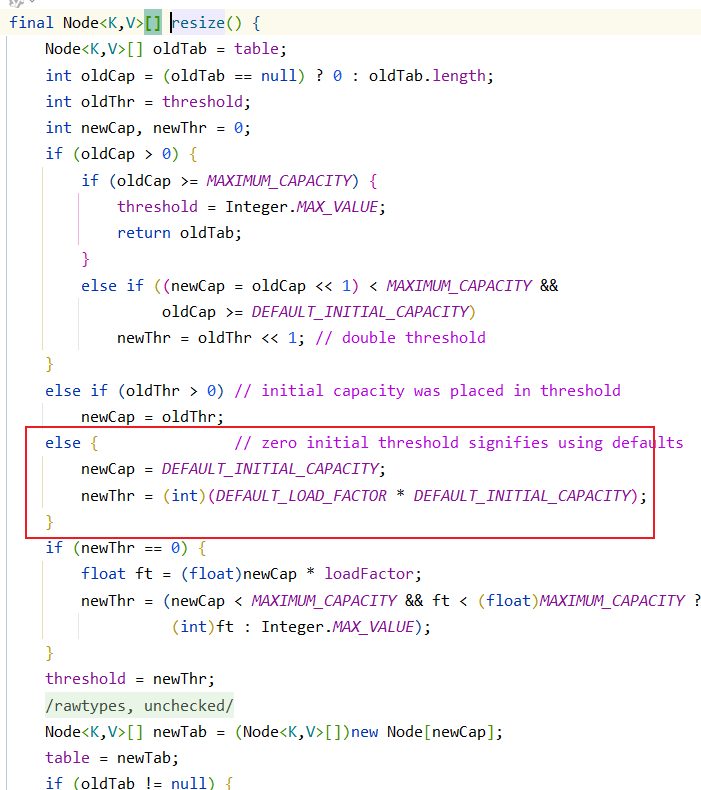
我们查看到oldTable实际上就是我们的table成员变量.很明显,oldCap 与 oldThr应该为0(调用无参构造时),
所以此时会进入红框的代码,查看到将默认的初始容量以及默认的阈值为默认容量乘以默认加载因子赋值给了newCap与newThr.再看接下来的

此时我们才看到newTab被进行了初始化,赋予了空间,并赋值给了table.此时才完成了HashMap容量的初始化.
随后返回
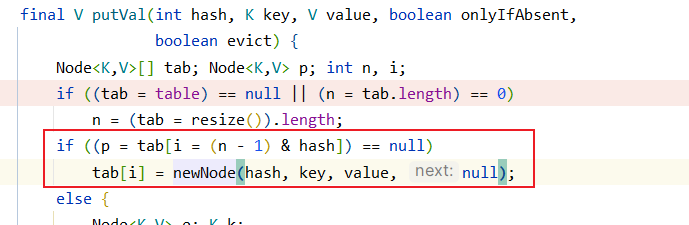
将resize后的长度赋给了n,然后利用 数组长度 - 1 与 哈希值做与运算得到数组下标的映射,将值赋给p,判断是否为null,为null则直接给这个槽位附上一个新的结点.
这里补充一下Node结构,查看下图

查看Node结构,我们也能发现我们调用put,put调用putVal时,传参本质就是在拼凑这个Node值.
我们再来查看放完值后执行了哪些流程
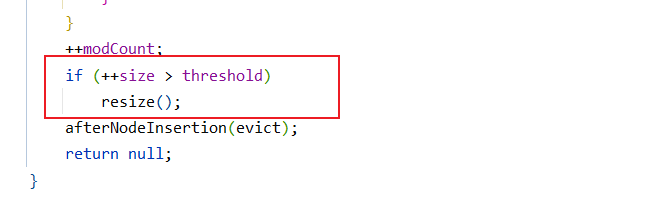
我们发现这里会对modCount++,最主要是我们在添加完元素之后,会进行判断现在Map中存放元素的数量是否达到阈值,如果达到,再次调用了resize扩容操作.也就是说,我们是在放完元素之后才去判定是否需要进行扩容,而不是放元素之前去判断是否需要扩容.
我们再去查看一下对应resize的代码
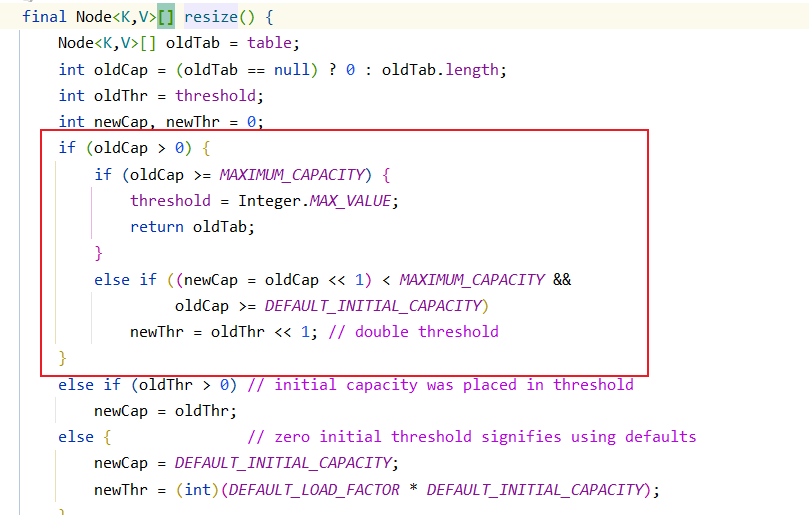
这里也就是判断,原哈希桶是否已经大于最大容量的限制,如果大于设置阈值为整数最大值,返回原来的哈希表(达到最大容量后不会再进行扩容).否则便把数组容量以及阈值重新扩容到原来的2倍.
2.2.2 链表与树化扩容
重点是接下来的过程,如何将原来的哈希表复制到新的哈希表中,我们来看看源码怎么执行的
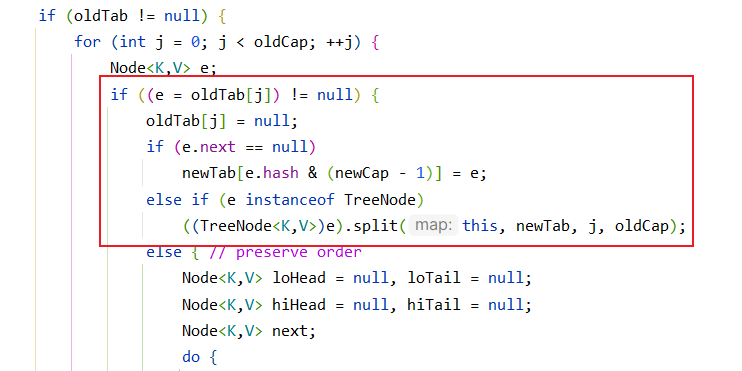
首先,将当前数组中的元素赋给e,判断是否为null,为null说明当前此处没有元素直接结束.如果有,将当前数组中j索引处设置为null,判断e有没有下一个结点,如有没有,则直接将当前结点重新进行 (数组长度 - 1) & e.hash 运算,将其转移到新的哈希表中.
否则,判定是否为树节点,如果是则走树节点的扩容赋值过程.
如果不是树节点,则就是链表结点,将会以链表的扩容赋值过程实现.
我们先看看链表结构是怎么实现扩容复制转移的.

我以一张图来表明链表复制转移的过程
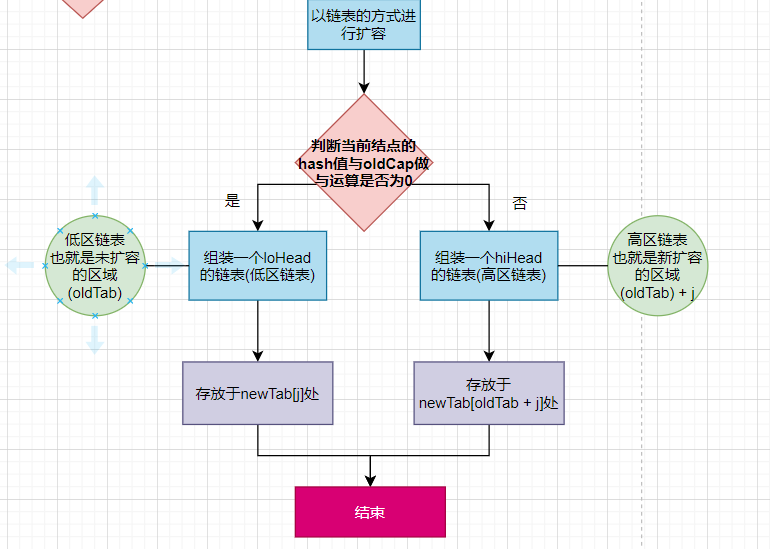
我们再来看看树结构是如何进行扩容赋值的

发现没有,几乎与链表的形式一模一样,所以可能猜想,链表结构转为红黑树后,红黑树内部可能还存在着原来链表结构的关系,这里依旧可以使用链表遍历的形式,不过我现在还没有证实,只是一个猜想.
我们再看后面是怎么处理的

它会进行判定,如果当前树结构的节点小于等于退化阈值,则会调用退化方法,将红黑树退化成链表.如果不是,则将这样的一个结点放入新容器中,不过这里我们查看, 放完之后,它调用了loHead.treeify()方法,说明它将以这样一个头结点的结构进行树化了,这更加说明我的猜想应该是正确的.
画一张图来总结一下树化扩容赋值的过程.
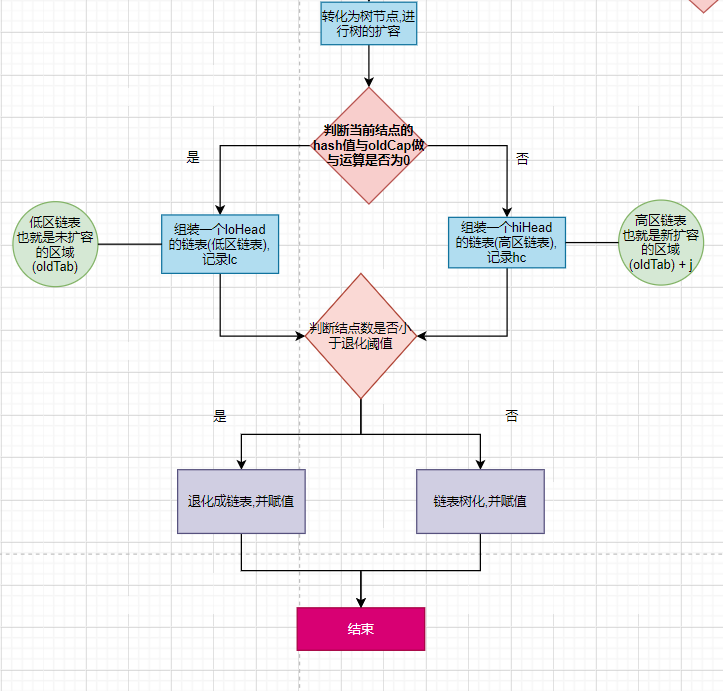
2.3 演示扩容现象
我们可以查看一下,扩容产生的现象,我们尝试放入13个元素,来查看HashMap中的table属性的长度是否为扩容后的32大小.测试代码如下
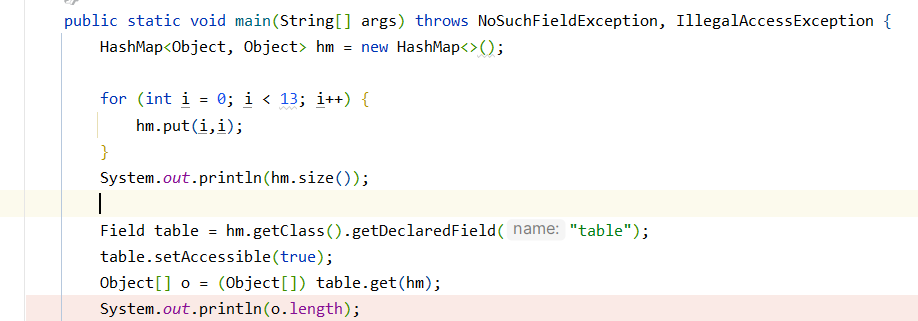
debug运行,查看测试结果,查看到已完成对应的扩容.
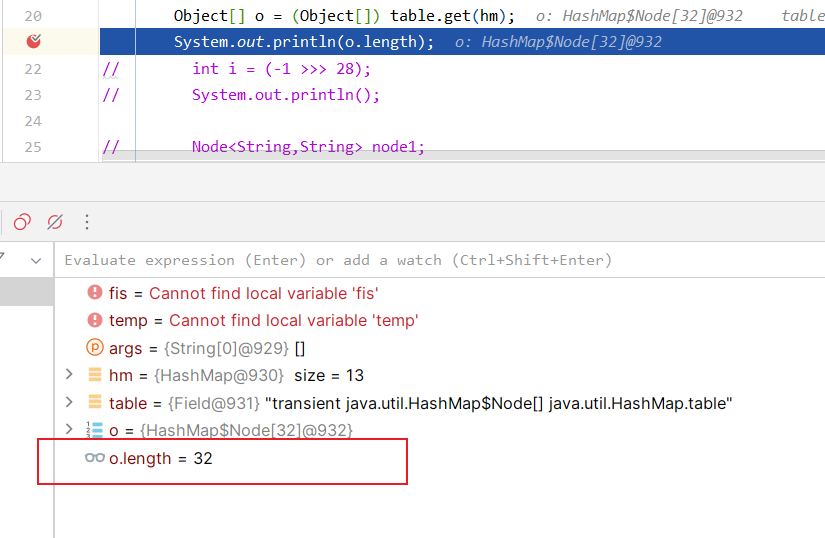
2.4 put过程
前面我们已经完成了扩容现象的观察.还没有仔细看看put的过程.回过头查看一下具体执行的流程.
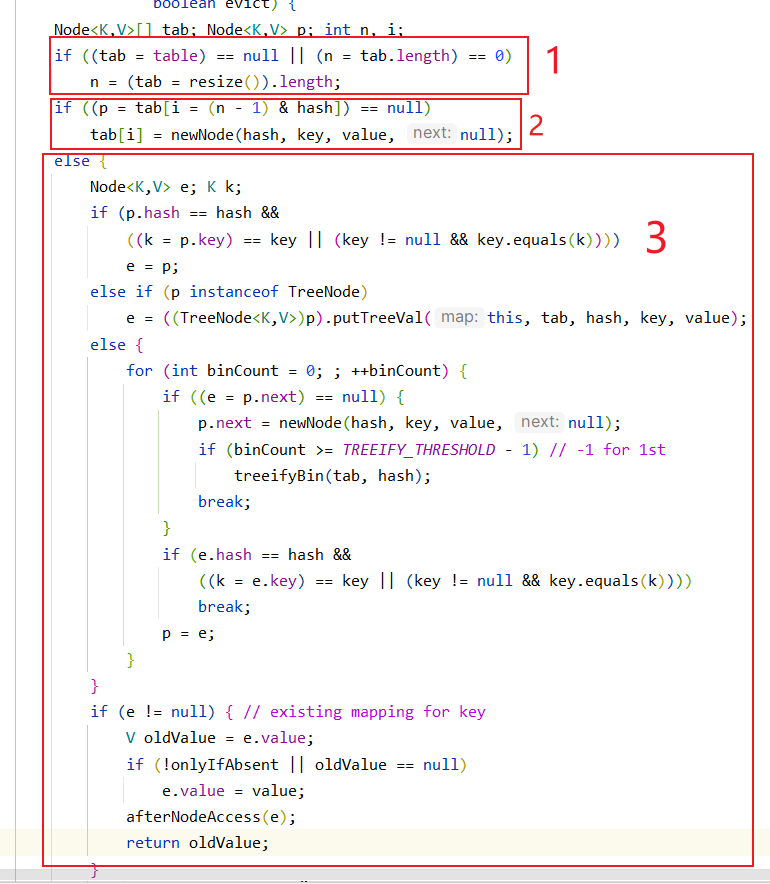
在前面的过程中,1阶段我已经解释过,我们来查看后面的2,3阶段.
第2阶段实际上就是判断 (数组大小 - 1) & key.hash 索引处有没有结点,如果没有,直接放入.
如果有,将进行链表或者树两种结构的判断来决定已什么的遍历方式来存放结点.

三. 取出
我们来查看get方法
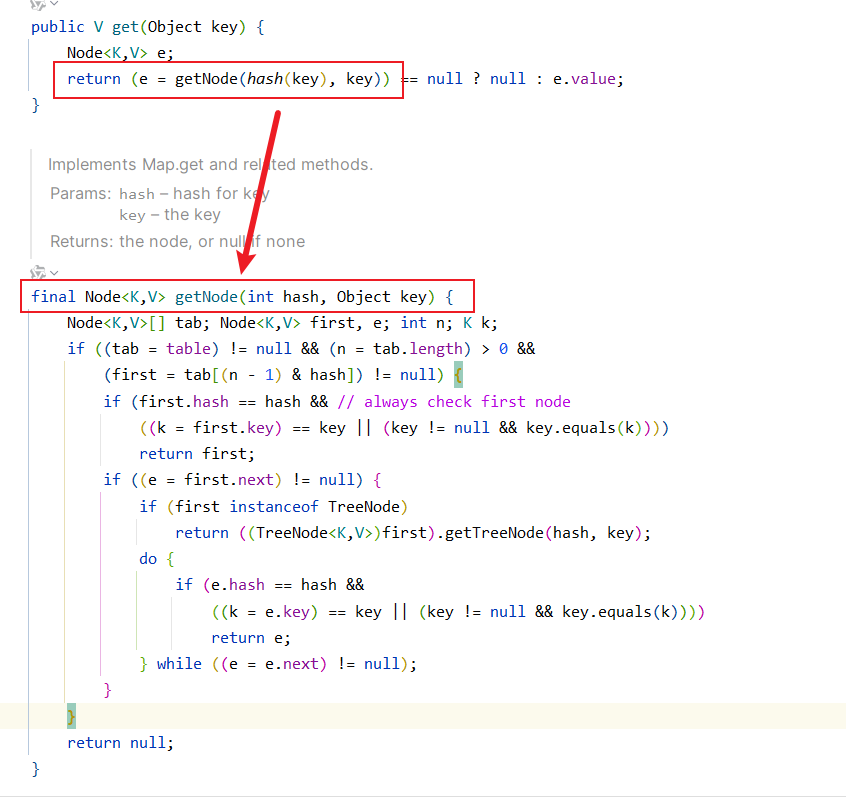
其实我们理解了存储的过程,这一块就很简单理解了
- 第一步: 判断当前哈希表是否被初始化, 判断当前查找元素的hash映射到数组中这个元素是否存在.不存在直接返回null
- 第二步: 存在则判断是否是相同的,相同则直接返回.
- 第三步: 不相同的话判断是树节点还是链表结点.如果是树则由树的遍历方式进行,如果是链表的话,就以链表的方式遍历.
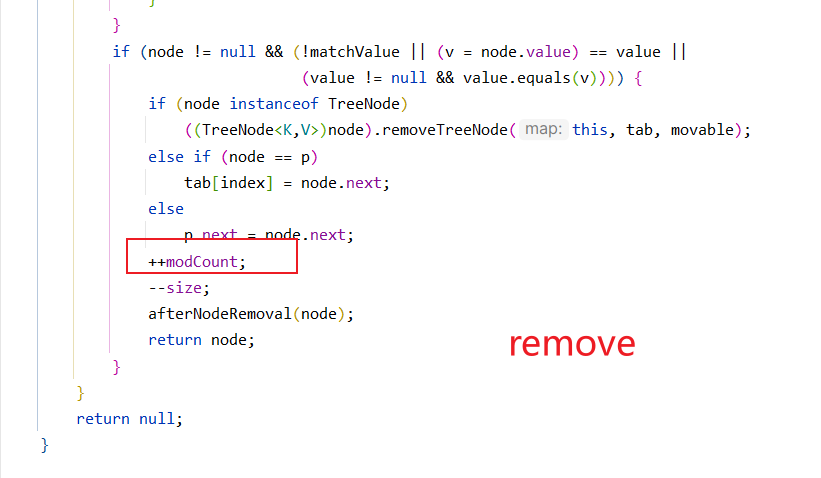
四. 删除
我们来查看一下remove方法,会发现一件好像很巧合的事情.
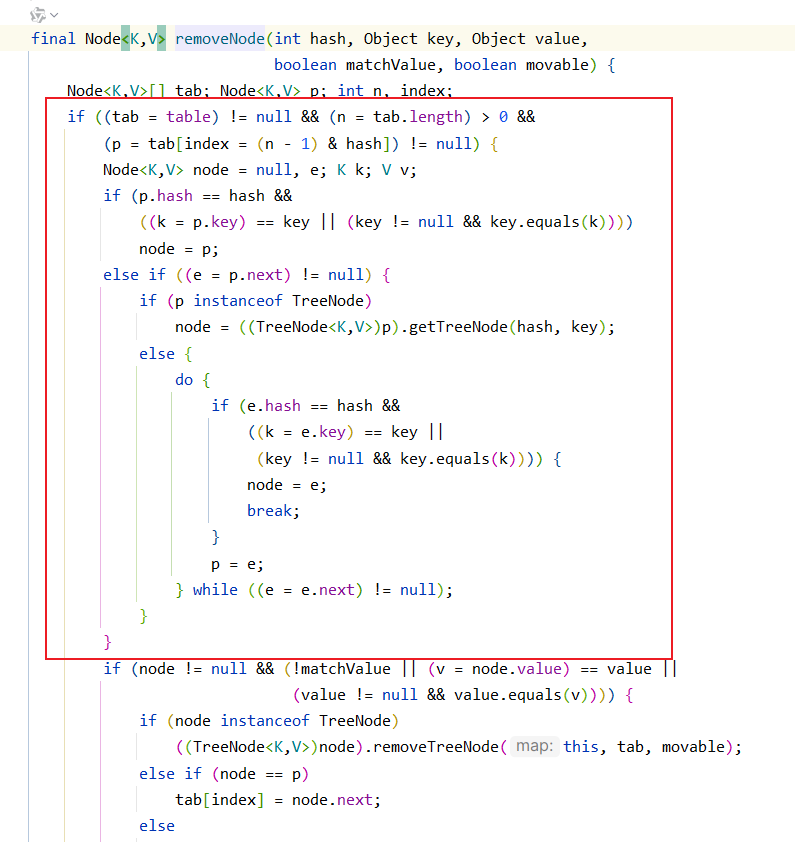
我们会发现红框处跟取出结点的代码一模一样,其实删除或者修改也好,前提都得找到对应的结点,所以这里才有一模一样的代码.
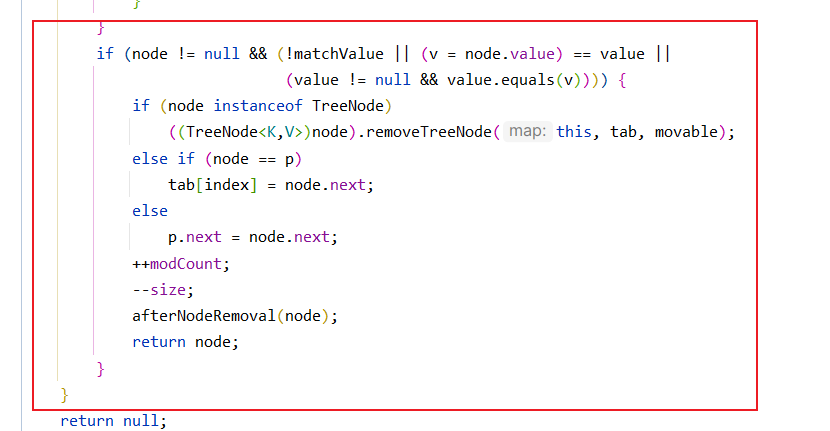
而后续操作还是老掉牙的一套,是红黑树结点则以红黑树的方式来删除.如果node == p(意思就是查找的元素就是数组上的元素), 直接让此数组索引处存放这个结点的下一个结点. 其他情况,那就说明是链表结构的删除结点,这里的p代表的是删除结点的前驱节点,所以只需要 p.next = node.next即可.
五. 快速失败
我们之前在查看源码时,我们观察到还有一个属性modCount.其实这个就是记录我们操作map的次数,但是呢,这里会出现一个问题.
无论是put方法还是remove的方法,我们观察到都会使modCount++.
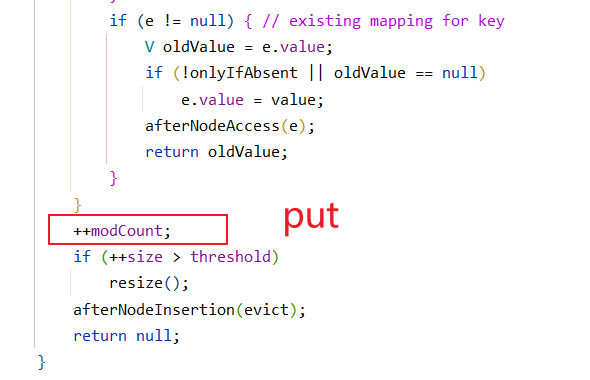
而如果我们采用HashMap中重写的foreach的方法遍历我们可以查看到

或者是采用EntrySet的迭代器遍历

我们都会发现有一段逻辑,在执行我们的遍历逻辑的前后,会有执行后的modCount 与执行前的mc值的比较,如果不等于,就会抛出异常.
其实也就是告诉我们,如果在使用这两个方式遍历时,不能使用map中的put或者remove方法,否则会抛出这样的异常.那有时候我们确确实实需要遍历时删除元素呢?
两种方式
删除时我们可以不用调用map的remove的方法,而是调用迭代器的remove的方法
或者采用最普通的for循环遍历,将map大小提出来,再进行遍历.