当前位置：首页 > news >正文

临床预测模型-静态诺模/列线图(Nomogram)+校准曲线(Calibration)分析学习

news 2024/11/14 13:19:21

诺模图（Nomogram），也被称为列线图，是一种图形化的计算工具，用于通过将多个变量的影响集成到一个单一的数值评分上，以预测某个特定事件的概率。这种工具常用于医学领域，尤其是在肿瘤学中，用于评估患者的疾病预后、生存率等。

图标的概念很简单，解释也很简单，代码也很简单 hhhh

校准曲线的概念之前也有聊过，可见推文：临床预测模型概述5-临床预测模型评价指标(区分度，校准度和临床决策曲线）https://mp.weixin.qq.com/s/pHVwjQd2Se3nKl601j1meg

分析流程-静态诺莫/列线图/Nomogram

1.导入

rm(list = ls())
library(stringr)
library(survival)
library(survminer)
proj <- "ttt"
load('data.Rdata')

2.数据预处理

colnames(meta)
variables <- c("cluster", "gender", "neoadjuvant")
meta <- cbind(meta[,c(1:3)],meta[,c("cluster", "gender", "neoadjuvant")])dat <- meta
dat <- na.omit(dat)
dim(dat)
# [1] 493   6# 对变量进行因子化
dat$cluster <- factor(dat$cluster,levels = c("1","2"))
dat$gender <- factor(dat$gender,levels = c("FEMALE","MALE"))
dat$neoadjuvant <- factor(dat$neoadjuvant,levels = c("No","Yes"))

2.诺模图-rms

library(rms)
dat$OS.time = dat$OS.time*30
dd <- datadist(dat)
options(datadist="dd")# 套用代码时需要修改下面这行公式~后面的部分
mod <- cph(Surv(OS.time, OS) ~ cluster + gender + neoadjuvant ,data=dat,x=T,y=T,surv = T)surv<-Survival(mod) 
m1<-function(x) surv(365,x)
m3<-function(x) surv(365*3,x)
m5<-function(x) surv(365*5,x)x<-nomogram(mod,fun = list(m1,m3,m5),funlabel = c('1-y survival','3-y survival','5-y survival'),lp = F)
plot(x)

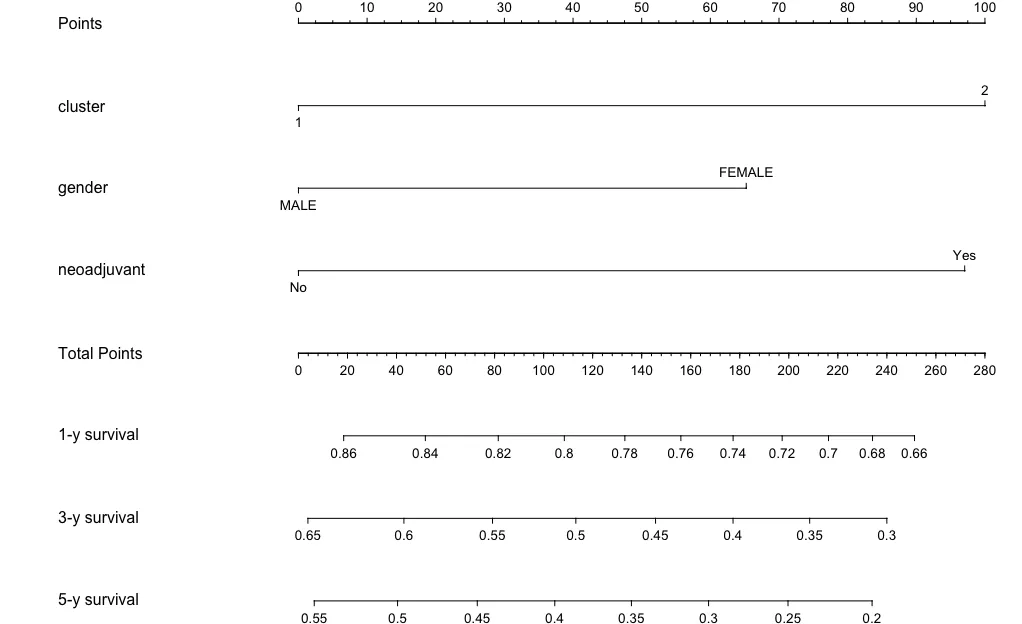
诺模图-regplot

library(regplot)
library(survival)
mod2 <- cph(Surv(OS.time, OS) ~ cluster + gender + neoadjuvant,data=dat,x=T,y=T,surv = T)# 第一类
regplot(mod2,failtime = c(365,365*3,365*5), plots = c("no plot","no plot"),points = T,prfail = T)# 第二类-显示某一个样本
regplot(mod2,observation=dat[1,],  # dat代表传入的数据矩阵obscol = "#326db1",failtime = c(365,365*3,365*5), plots = c("no plot","no plot"),points = T,prfail = T)# 第三类-增加分布情况图形
regplot(mod2,observation=dat[1,], failtime = c(365,365*3,365*5), plots = c("bars","boxes"),points = T,prfail = T)

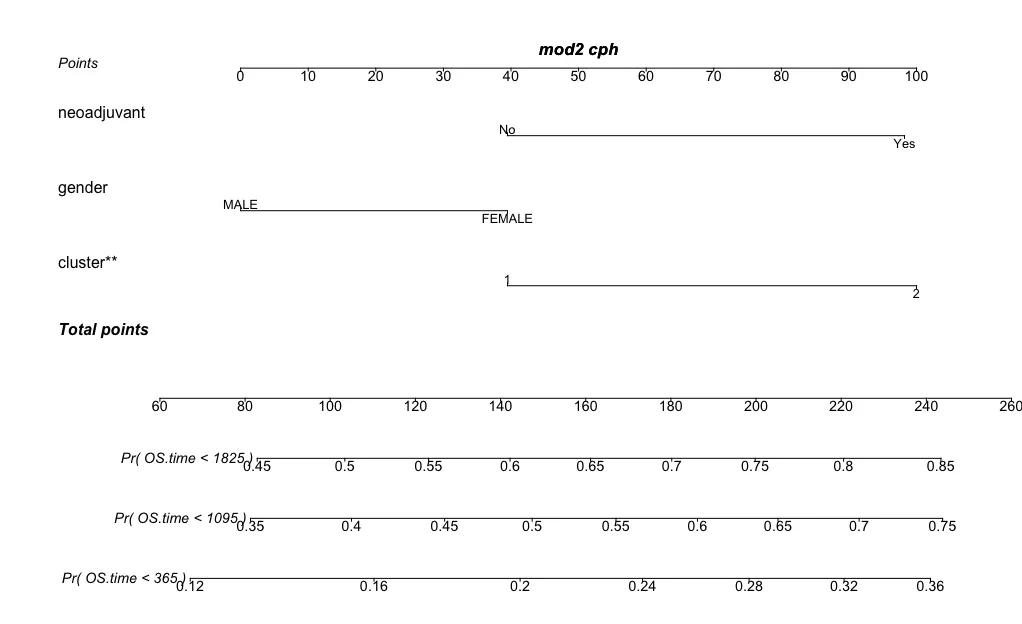
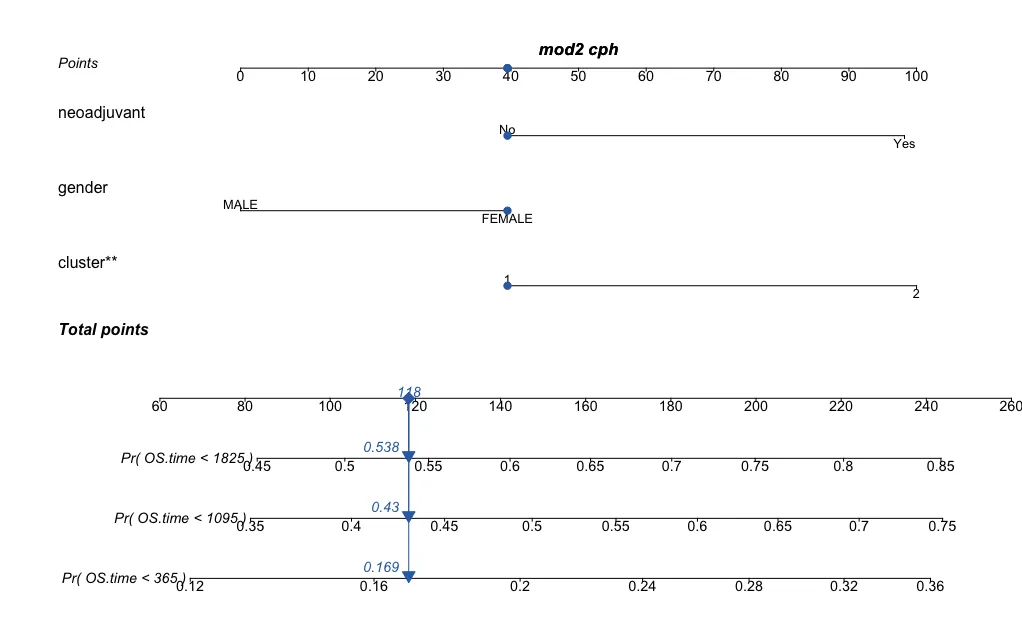
下面两张图就是随机挑选了一个样本，然后进行分值计算。比如这个样本是neoadjuvant=0代表了40分，性别为FEMALE代表了40分，cluster=1代表了40分，然后进行总分计算(总分是118的原因是上面实际的点没有确凿在40分，稍为有点区别，但是影响不大，大概就是120分)，然后对应到下面的刻度轴上就可以得到1年的死亡率是16.9%，3年的死亡率是43%，5年的死亡率是53.8%。

这个图没有什么花头，就是增加了一点图形样式。

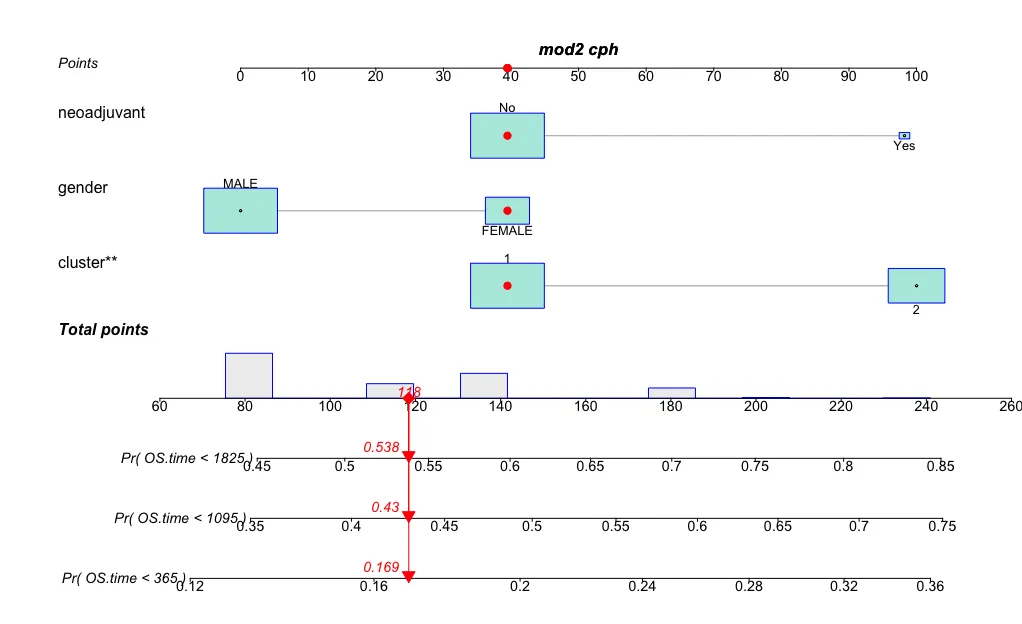
分析流程-校准曲线(Calibration)

1.导入

rm(list = ls())
library(stringr)
library(survival)
library(survminer)
proj <- "aaa"
load('data.Rdata')

2.数据预处理

colnames(meta)
variables <- c("cluster", "gender", "neoadjuvant")
meta <- cbind(meta[,c(1:3)],meta[,c("cluster", "gender", "neoadjuvant")])data <- meta
data <- na.omit(data)
dim(data)
# [1] 493   6# 如果是连续的代码，需要设置data
data$OS.time <- data$OS.time*30# 对变量进行因子化
data$cluster <- factor(data$cluster,levels = c("1","2"))
data$gender <- factor(data$gender,levels = c("FEMALE","MALE"))
data$neoadjuvant <- factor(data$neoadjuvant,levels = c("No","Yes"))# 数据分割 7:3,8:2 均可
# 划分是随机的，设置种子数可以让结果复现
set.seed(123)
ind <- sample(1:nrow(data), size = 0.7*nrow(data))
train <- data[ind,]
test <- data[-ind, ]

3.训练集

# 必须先打包数据
dd <- datadist(train)
options(datadist = "dd")# cph用于拟合Cox 比例风险回归模型
# lrm用于拟合logstic回归模型
f1 <- cph(formula =  Surv(OS.time, OS) ~ cluster + gender + neoadjuvant,data=dat,x=T,y=T,surv = T, time.inc=365)
cal1<- calibrate(f1, cmethod="KM", method="boot", u=365, m=50, B=1000)f2 <- cph(formula =  Surv(OS.time, OS) ~ cluster + gender + neoadjuvant,data=dat,x=T,y=T,surv = T, time.inc=365*2)
cal2 <- calibrate(f2, cmethod="KM", method="boot", u=730, m=50, B=1000)f3 <- cph(formula =  Surv(OS.time, OS) ~ cluster + gender + neoadjuvant,data=dat,x=T,y=T,surv = T, time.inc=365*3)
cal3 <- calibrate(f3, cmethod="KM", method="boot", u=1095, m=50, B=1000)data1 <- data.frame(Time = rep("1-year", nrow(cal1)),Predicted = cal1[,"mean.predicted"],Observed = cal1[,"KM"]
)data2 <- data.frame(Time = rep("2-year", nrow(cal2)),Predicted = cal2[,"mean.predicted"],Observed = cal2[,"KM"]
)data3 <- data.frame(Time = rep("3-year", nrow(cal3)),Predicted = cal3[,"mean.predicted"],Observed = cal3[,"KM"]
)all_data <- rbind(data1, data2, data3)
library(ggplot2)
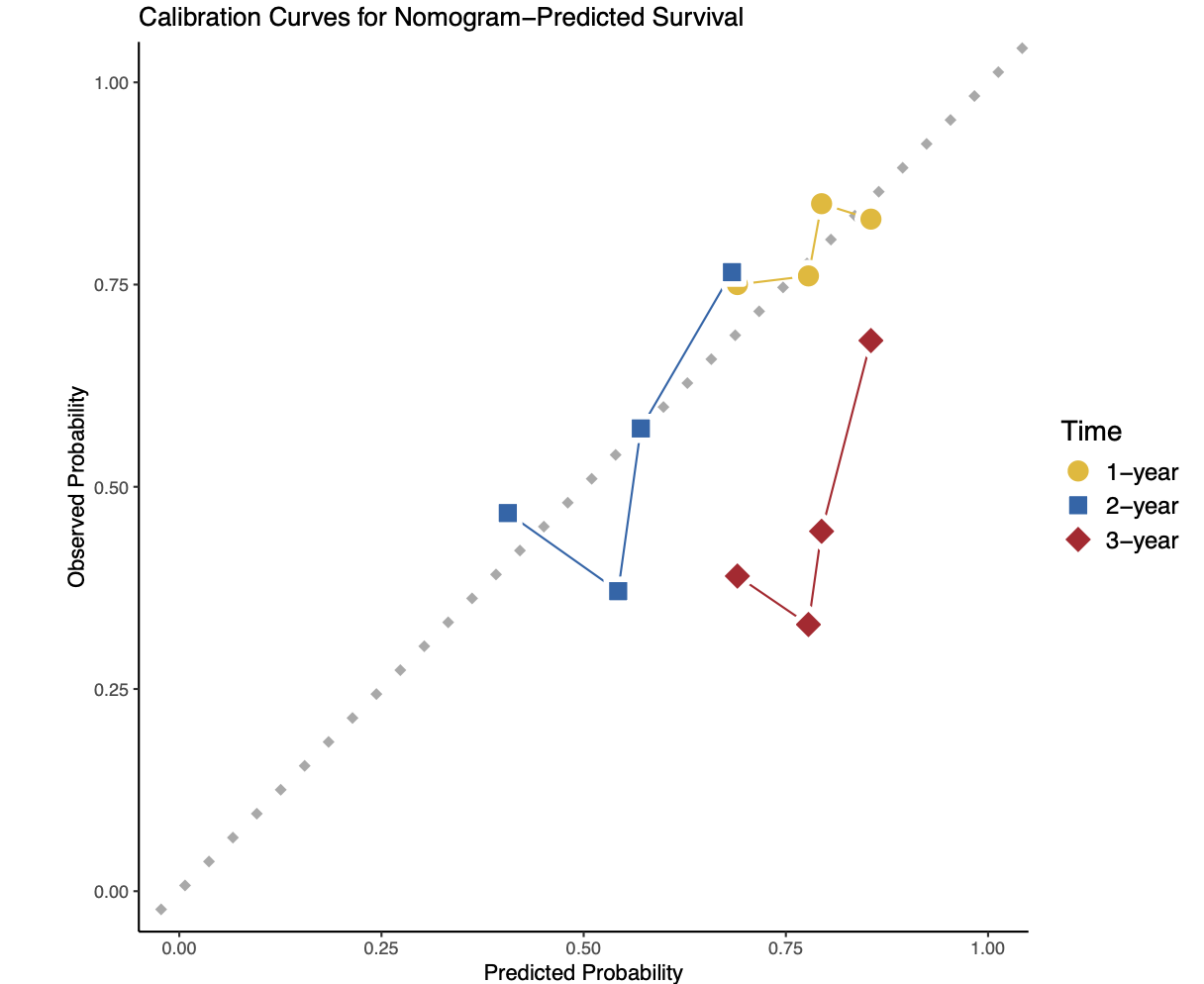
ggplot(all_data, aes(x = Predicted, y = Observed)) +geom_abline(intercept = 0, slope = 1, linewidth = 2,linetype = 3, color = "darkgrey") +geom_line(aes(color = Time)) + scale_color_manual(values = c("#e6b707", "#2166AC", "#B2182B")) + geom_point(aes(shape =Time,fill = Time),color = "white",size = 5,stroke = 2) +scale_shape_manual(values = c(21,22,23))+scale_fill_manual(values = c("#e6b707", "#2166AC", "#B2182B")) + labs(title = "Calibration Curves for Nomogram-Predicted Survival",x = "Predicted Probability",y = "Observed Probability",color = "Time") +xlim(0, 1) + ylim(0, 1) +theme_classic() + coord_fixed()+theme(legend.title = element_text(size = 14),legend.text = element_text(size = 12)) 
ggsave("Calibration.pdf",width = 9,height = 7)

4.验证集

# 必须先打包数据
dd <- datadist(test)
options(datadist = "dd")## 验校准曲线
# 1年
vadfcox1<-cph(Surv(OS.time,OS)~predict(f1,newdata = test),surv=T,x=T,y=T,time.inc = 365,data = test)
# 拟合calibrate
vadcal1<-calibrate(vadfcox1,cmethod = 'KM', method = 'boot',u = 365,m = 25,B = 500)# 2年
vadfcox2<-cph(Surv(OS.time,OS)~predict(f2,newdata = test),surv=T,x=T,y=T,time.inc = 365*2,data = test)
# 拟合calibrate
vadcal2<-calibrate(vadfcox2,cmethod = 'KM', method = 'boot',u = 365*2,m = 25,B = 500)# 3年
vadfcox3<-cph(Surv(OS.time,OS)~predict(f3,newdata = test),surv=T,x=T,y=T,time.inc = 365*3,data = test)
# 拟合calibrate
vadcal3<-calibrate(vadfcox1,cmethod = 'KM', method = 'boot',u = 365*3,m = 25,B = 500)data1 <- data.frame(Time = rep("1-year", nrow(vadcal1)),Predicted = vadcal1[,"mean.predicted"],Observed = vadcal1[,"KM"]
)data2 <- data.frame(Time = rep("2-year", nrow(vadcal2)),Predicted = vadcal2[,"mean.predicted"],Observed = vadcal2[,"KM"]
)data3 <- data.frame(Time = rep("3-year", nrow(vadcal3)),Predicted = vadcal3[,"mean.predicted"],Observed = vadcal3[,"KM"]
)all_data <- rbind(data1, data2, data3)
library(ggplot2)
ggplot(all_data, aes(x = Predicted, y = Observed)) +geom_abline(intercept = 0, slope = 1, linewidth = 2,linetype = 3, color = "darkgrey") +geom_line(aes(color = Time)) + scale_color_manual(values = c("#e6b707", "#2166AC", "#B2182B")) + geom_point(aes(shape =Time,fill = Time),color = "white",size = 5,stroke = 2) +scale_shape_manual(values = c(21,22,23))+scale_fill_manual(values = c("#e6b707", "#2166AC", "#B2182B")) + labs(title = "Calibration Curves for Nomogram-Predicted Survival",x = "Predicted Probability",y = "Observed Probability",color = "Time") +xlim(0, 1) + ylim(0, 1) +theme_classic() + coord_fixed()+theme(legend.title = element_text(size = 14),legend.text = element_text(size = 12)) 
ggsave("Calibration_test.pdf",width = 9,height = 7)

参考资料：

生信星球：https://mp.weixin.qq.com/s/d_gO7ORa_l3TEXfqTlgLQg
医学和生信笔记：https://mp.weixin.qq.com/s/o9OlvPjl6nP_9gVKasvY5Q https://mp.weixin.qq.com/s/zBqpXjTIG50crkVZAgYOoA https://mp.weixin.qq.com/s/akT45OaLSJgoh33UBzrIyQ

注：若对内容有疑惑或者有发现明确错误的朋友，请联系后台(欢迎交流)。更多内容可关注公众号：生信方舟

- END -

查看全文

http://www.mrgr.cn/news/69786.html