图形几何之美系列:仿射变换矩阵
“ 在几何计算、图形渲染、动画、游戏开发等领域,常需要进行元素的平移、旋转、缩放等操作,一种广泛应用且简便的方法是使用仿射变换进行处理。相关的概念还有欧拉角、四元数等,四元数在图形学中主要用于解决旋转问题,特别是在三维空间中绕任意轴的旋转,且四元数与仿射变换可以相互转换。”
本文仅对仿射变换进行介绍。
1.前言
仿射变换是一种结合了线性变换和平移的变换,不仅包括旋转、缩放等线性变换,还包括平移操作。
仿射变换具有简比不变性和交比不变性:
变换前是直线的,变换后依然是直线;
直线比例保持不变。
仿射变换可以用形如下图的4x4矩阵表示,即仿射变换矩阵。
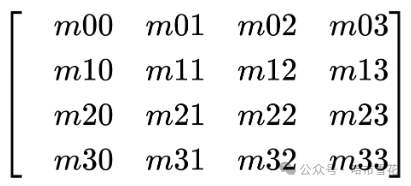
注意
如果没有特殊说明,本文所述仿射变换矩阵皆为矩阵乘列向量/点方式的,即把向量和点作为4x1矩阵参与运算,如下图所示。
有相关的书籍或程序采用的是将向量和点作为1x4矩阵形式以向量/点x仿射变换矩阵的形式进行运算,但这不是重点,你只需要知道这是一种方式选择即可,就像左手还是右手坐标系或者是Z-Up还是Y-Up一样。
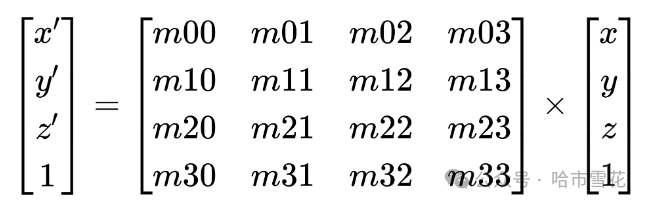
2.仿射变换矩阵
回想一下,在图形学中的基础数据为点(Point)、向量(Vector),线可以由点连接而成,轮廓可以由首尾相连的线集合构成,面可以由轮廓构成,而实体可以由构成闭合关系的若干面表示,法向可以表示为向量。
在图形学中对元素(向量、点、线、面、实体等)进行空间姿态变换时实际上是对其基本构成数据(向量、点)进行处理的,同时保持这些数据的拓扑关系不变,想象一下一个立方体经过空间平移和旋转变换之后仍然是立方体,虽然其顶点和面法向进行了变换,但数据的拓扑关系不变。
补充:
实体结构由几何数据和拓扑数据组成。几何数据描述实体的基本形状,包括点、线、面、体的信息。拓扑数据则描述了物体各部分之间的连接关系,确保物体的几何形状在空间中的唯一性和一致性。
如一个六边形轮廓包含6个顶点,但仅有6个顶点尚不足以表示该六边形,还需要点之间的连接关系,比如由v0连接v1而不是v4,这就是拓扑关系数据的作用。对其进行空间姿态变换,其几何数据发生了姿态变换,但数据的拓扑关系不变,仍由v0连接v1而不是v4。
提示:
上述六边形的几何数据为6个顶点,拓扑数据为这些顶点的连接关系。
看到这里你已经知道物体的空间姿态变换实际上是对构成其的点、向量数据进行空间姿态变换,而数据间拓扑关系保持不变。
点和向量均由x、y、z三个要素构成,区别是向量是方向而点是具体位置。为用统一且适合的仿射变换矩阵来处理点和向量,增加了齐次坐标的概念,点可以表示为[x,y,z,1],向量可以表示为[x,y,z,0]。
对上述点和向量的矩阵表示形式进行转置得到4x1矩阵,学习过线性代数的你容易了解4X4矩阵乘4x1矩阵的结果依然是4x1矩阵,我们可以用4x4矩阵表示仿射变换矩阵,其构成如下图所示,

提示:
有关齐次坐标的概念和讲解可参考相关书籍如《3D数学基础:图形和游戏开发(第2版)》。
矩阵左上角的3x3部分为实体各轴的空间姿态变换,可以表示缩放、旋转、镜像、非均匀变换,右侧竖向3个元素表示平移距离,可以表示平移,对第四行元素赋值[0,0,0,1]即可,
这样仿射变换矩阵便构造完成。
3.仿射变换矩阵的构成和原理
如果只了解应用不了解原理是不可靠的,我们需要经常性的与仿射变换矩阵打交道,如果我们继续从事图形几何方面学习研究和工作的话。
从相对角度看,物体空间姿态变换也可以认为是空间坐标系发生了变换,而物体没有发生相对变化,比如乘客系好安全带坐在车内,车在跑,乘客相对车没有变化,是车子(坐标系)发生了变换。
或者认为物体局部坐标系(物体坐标系)没有变化,而其在世界坐标系中的坐标发生了变化,在变化后,物体坐标系值(在世界坐标系中的值)改变了,但物体相对于其物体坐标系没有变化。
原始坐标系基向量分别为:baseX(1,0,0)、baseY(0,1,0)、baseZ(0,0,1),原点为origin(0,0,0)。对该坐标系进行变换得到baseX'、baseY'、baseZ'、origin',组成变换后的姿态坐标系。
如下图所示,我们注意到点P'相对于姿态坐标系坐标依然是(Px,Py,Pz),虽然P'在原始坐标系中的坐标发生了变化。
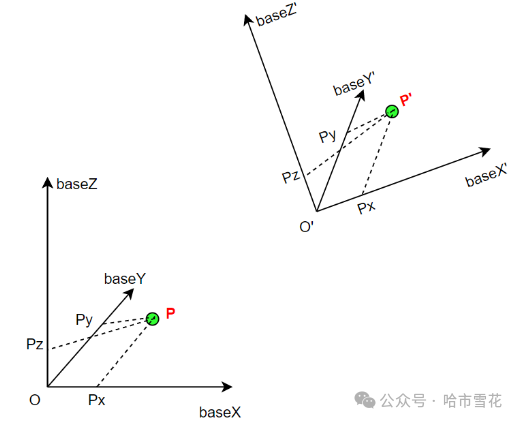
当前坐标系为TrsWorld(O,baseX,baseY,baseZ),点P(在当前坐标系)坐标为P(Px,Py,Pz),对点P进行空间姿态变换到P'(Px',Py',Pz')位置。
为便于理解,我们对TrsWorld进行同样的姿态变换得到姿态坐标系Trs1(O',baseX',baseY',baseZ'),点P'在坐标系Trs1中的坐标依然是(Px,Py,Pz),这时我们注意到Trs1的baseX'在TrsWorld的三个坐标轴中有分量,即baseX'[0]、baseX'[1]、baseX'[2]。baseY'、baseZ'及O'在TrsWorld的三个坐标轴中同样有分量。这样点P'在TrsWorld中的X坐标Px'(即在baseX的分量)须考虑baseX'、baseY'、baseZ'分别在baseX中的分量baseX'[0]、baseY'[0]、baseZ'[0]。
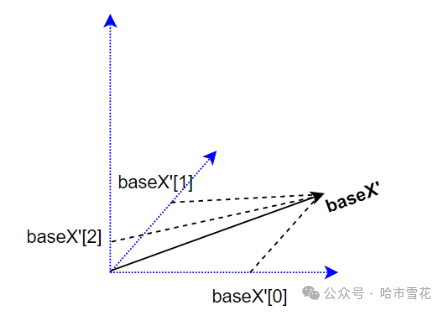
注意
姿态坐标系Trs1为我们虚拟出来的过程坐标系,便于理解仿射变换矩阵的构成和原理,实际可能并不存在该坐标系。
上述话题总结表述:点P经过空间姿态变换得到点P',求P到P'对应的仿射变换矩阵,点P和P'都是基于同一个坐标系的度量。
点P'可以由点O'+向量O'P'得到,O'P'在Trs1中坐标为(Px,Py,Pz),由上可知:
-
Trs1中的Px在TrsWorld的三个坐标轴的分量分别为PxbaseX'[0]、PxbaseX'[1]、Px*baseX'[2];
-
Trs1中的Py在TrsWorld的三个坐标轴的分量分别为PybaseY'[0]、PybaseY'[1]、Py*baseY'[2];
-
Trs1中的Pz在TrsWorld的三个坐标轴的分量分别为PzbaseZ'[0]、PzbaseZ'[1]、Pz*baseZ'[2];
-
Trs1中的O(0,0,0)在TrsWorld的三个坐标轴分量分别为O'[0]、O'[1]、O'[2];
这样,
-
Px'= PxbaseX'[0] + PybaseY'[0] + Pz*baseZ'[0] + O'[0];
-
Py'= PxbaseX'[1] + PybaseY'[1] + Pz*baseZ'[1] + O'[1];
-
Pz'= PxbaseX'[1] + PybaseY'[2] + Pz*baseZ'[2] + O'[2];
我们用矩阵形式表示,
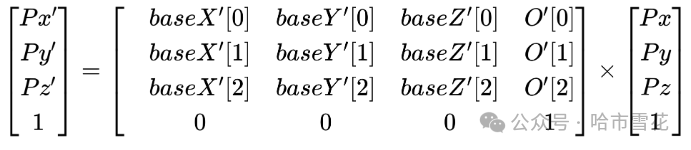
矩阵左上角的3X3部分的三个列向量实际是姿态变换后三个基向量(在原始坐标系中)的坐标。
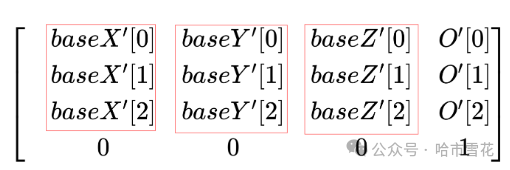
细心的你可能已经发现在仿射矩阵乘向量时,其右侧表征平移部分不起作用,是的,对向量进行偏移不会改变向量值,这通过增加齐次坐标的概念来实现。
仿射变换矩阵可以作用于点、向量以及由他们构成的几何数据。
4.局部坐标转世界坐标
另一个经典话题是物体由局部坐标系转为世界坐标系,我们来看一看。在这个话题中,物体在局部坐标系中的度量、局部坐标系在世界坐标系的度量均已知,然后求物体在世界坐标系中的度量。
下述场景切合当前话题,
-
建模过程中放置构件场景,设置构件的放置点、旋转角度、缩放比例、是否镜像等;
-
求空间中构件在世界坐标系中的坐标,在已知构件的局部坐标和局部坐标系在世界坐标系中的姿态;
-
多坐标系场景中,如Revit的构件坐标系、项目坐标系、共享坐标系中,已知构件在项目坐标系中的坐标、项目坐标系在共享坐标系中的度量,求构件在共享坐标系中的坐标,方便和其他项目在同一共享坐标中进行合模。
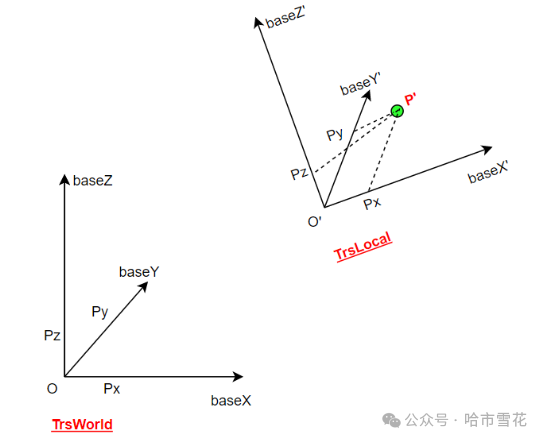
我们基于上述场景2进行分析,继续沿用上述章节中的图片,但我们忽略点P,以P'为目标进行分析,我们可以对上述章节过程进行截取,可以认为上图中的姿态坐标系Trs1即为局部坐标系,求P'在世界坐标系TrsWorld中的坐标。
这相对简单了些,已知Trs1在TrsWorld中的姿态(即度量)(O',baseX',baseY',baseZ')、点P'在Trs1中的坐标(Px,Py,Pz),求P'在TrsWorld中的坐标。直接上结果把,
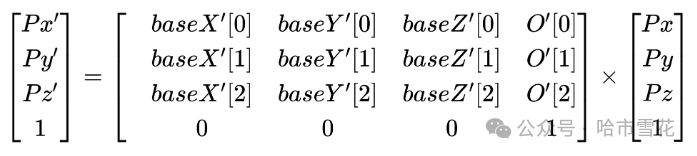
如果基于上述场景1进行分析,那可以完全沿用图片且不用忽略点P。
思考
为什么我们构造的局部坐标系转世界坐标系的仿射变换矩阵和2.1节中姿态变换矩阵是一样的?
请读者自行思考以加深理解。
欢迎关注作者。图形几何之美系列 将继续更新......
5.写在后面
图形几何、数据处理、并行计算相关研究和研发,公众号:geometrylib,欢迎交流。
_________哈市雪花__________
