算法通关（4）-- 前缀树

前缀数原理和代码

原理

前缀树（Trie树），也称为字典树，是一种用于高效存储和检索字符串的数据结构。它是一种树形结构，能够利用字符串的公共前缀来减少存储空间和查询时间。

现在有“acb”,"cba","acc"，"ac"四个字符串，利用这四个字符串构出一颗前缀树。根节点不包含任何字符，是所有字符串的公共前缀；每个节点包含pass信息，代表加节点的时候路过了几次，还有一个end信息表示多少个字符串是以当前字符串结尾的。举个例子：
 

 插入完成后得到的树形结构：

那么现在问：字符串acb出现了几次。由前缀树的end的得知出现了1次，当然，哈希表也能做到，但是如果说以ac开头的字符串出现了几次，这样子哈希表并不能做到，前缀树可以，出现了3次，依据p值 。

没有路就新建节点，有路就复用节点

那么前缀树的优缺点就体现出来了
优点：根据前缀信息选择树上的分支，可以节省大量空间。
缺点：比较浪费空间，和总字符数量有关，还和字符的种类有关

类的方式实现

需要实现的方法：

1.Trie() 初始化前缀树对象

首先是每个节点，需要pass，以及end来进行记录，nexts数组记录该节点后应该连接哪一个点

class TrieNode {
public:int pass;			// 通过该节点的字符串数量int end;			// 以该节点为结尾的字符串数量vector<TrieNode*>nexts;	// 子节点指针数组TrieNode() :pass(0), end(0), nexts(26, nullptr) {};
};

前缀树初始化的时候就是把头节点建出来就可以了。

private:TrieNode root;public:Trie() {root = TrieNode();}

2.void insert(String word)字符串插入
 

void insert(const string &word) {// 向前缀树插入wordTrieNode* node = &root;// 根节点路过++node->pass++;// 遍历每个字符for (char c : word) {// 'a' --> 0// 'b' --> 1// ...// 'z' --> 25int index = c - 'a';if (node->nexts[index] == nullptr) {// 没有就新建node->nexts[index] = new TrieNode();}// 有就复用node = node->nexts[index];node->pass++;}// 字符遍历完了，end++node->end++;
}

3.int search(String word) 返回前缀树字符串word的实例个数

int search(const string &word) {// 返回前缀树中字符串word的实例个数TrieNode* node = &root;// 一个一个字符寻找for (char c : word) {// 按照插入的indexint index = c - 'a';// 没找到，返回0，表示0个if (node->nexts[index] == nullptr) {return 0;}// 找到了，继续走node = node->nexts[index];}// 走完了，返回endreturn node->end;
}

4.int prefixNumber(String prefix)返回前缀树以prefix为开头的个数

和search相同，只是返回值不同

int predixNumber(const string& prefix) {// 返回前缀树以prefix为前缀的字符串个数TrieNode* node = &root;for (char c : prefix) {int index = c - 'a';if (node->nexts[index] == nullptr) {return 0;}node = node->nexts[index];}return node->pass;
}

5.void delete(String word)移除字符串word

要删除某个字符串，首先要查询一下前缀树中是否有该字符串，有字符串才能够删除

// 单词是否插入过前缀树
bool countWord(const string &word) {TrieNode* node = &root;for (char c : word) {int index = c - 'a';if (node->nexts[index] == nullptr) {return false;}node = node->nexts[index];}// pass大于0，才能表示插入过return node->pass > 0;
}void to_delete(const string &word) {// 从前缀树移除字符串word// 存在才移除if (countWord(word)) {// 插入过前缀树TrieNode* node = &root;node->pass--;for (char c : word) {int index = c - 'a';if (--node->nexts[index]->pass == 0) {// a->b->c//	   ->e->f 现在删除a,b,e,f,当看到--e为空，直接附空，后面不用看了delete node->nexts[index];  node->nexts[index] = nullptr;return;}// 如果不是，沿途的每个pass都--node = node->nexts[index];}node->end--;}else {cout << "没有 " << word << " 这个单词！ " << endl;}
}

静态数组的方式实现

先申请一个足够大的空间Tree,假设整个字符集只有三种字符a,b,c，那么申请出的二维数组为Tree[N][3],初始全为0，3代表去三个字符的路

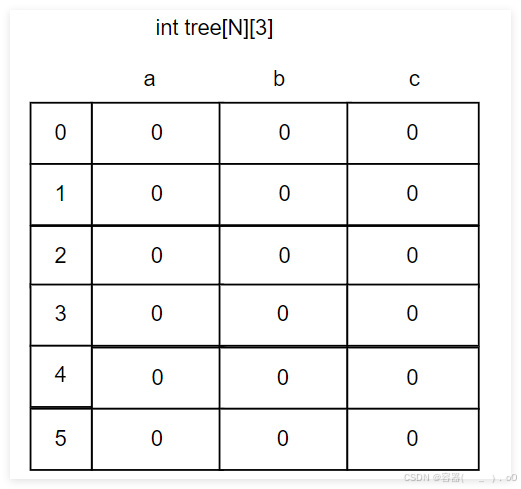
图中的1，2，3... 可以看作节点编号 
还有一个计算器cnt,表示节点编号，初始值为1，赋给根节点，当插入字符串“acb”时，对于第一个字符'a'，走第一列，看到（a,1）位置为0，表示没有路，cnt++变成2，那么此处的0变成2；对于'c'，2号节点走向c,那么（c,2）位置的0变成3;同理，（b,3）位置变成4;

 再次插入"ab",a是有的（1编号的a位置是2），b是没得（2编号的b位置是0），因此可以得到如下图：

 字典树的实现_牛客题霸_牛客网
代码如下：

public static int MAXN = 150001;// 26个英文字母public static int[][] tree = new int[MAXN][26];// end和pass申请空间，存每个节点public static int[] end = new int[MAXN];public static int[] pass = new int[MAXN];// 每个节点的编号public static int cnt;// 头节点public static void build() {cnt = 1;}public static void insert(String word) {int cur = 1;pass[cur]++;for (int i = 0, path; i < word.length(); i++) {// 找编号path = word.charAt(i) - 'a';if (tree[cur][path] == 0) {// 找不到新建tree[cur][path] = ++cnt;}// 找到利用cur = tree[cur][path];pass[cur]++;}end[cur]++;}public static int search(String word) {int cur = 1;for (int i = 0, path; i < word.length(); i++) {path = word.charAt(i) - 'a';// 路断了if (tree[cur][path] == 0) {return 0;}cur = tree[cur][path];}return end[cur];}public static int prefixNumber(String pre) {int cur = 1;for (int i = 0, path; i < pre.length(); i++) {path = pre.charAt(i) - 'a';if (tree[cur][path] == 0) {return 0;}cur = tree[cur][path];}return pass[cur];}public static void delete(String word) {if (search(word) > 0) {int cur = 1;for (int i = 0, path; i < word.length(); i++) {path = word.charAt(i) - 'a';if (--pass[tree[cur][path]] == 0) {tree[cur][path] = 0;return;}cur = tree[cur][path];}end[cur]--;}}// 初始化全部是0public static void clear() {for (int i = 1; i <= cnt; i++) {Arrays.fill(tree[i], 0);end[i] = 0;pass[i] = 0;}}public static int m, op;public static String[] splits;public static void main(String[] args) throws IOException {BufferedReader in = new BufferedReader(new InputStreamReader(System.in));PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));String line = null;while ((line = in.readLine()) != null) {build();m = Integer.valueOf(line);for (int i = 1; i <= m; i++) {splits = in.readLine().split(" ");op = Integer.valueOf(splits[0]);if (op == 1) {insert(splits[1]);} else if (op == 2) {delete(splits[1]);} else if (op == 3) {out.println(search(splits[1]) > 0 ? "YES" : "NO");} else if (op == 4) {out.println(prefixNumber(splits[1]));}}clear();}out.flush();in.close();out.close();}

相关题目

题目1：

接头密匙_牛客题霸_牛客网

将得到的新数组进行前缀树的插值，为了正确的插入1，而不是11，字符串改为1#1#1#1#1#,表示相隔一个字符终止一次，将所有的a数组的每个小数组的值构成前缀树，那么利用b数组中的字符串查找b相关的字符串出现了几次，每查一个b中的小数组记录一次，总记录得到的就是答案。
那么如果a数组的值相差很大呢，例如[1,1000,10000],得到的是[999,9999],那么是不是开10000个，不能，这样子有空间浪费；我们应该将数字转为字符串,"999#","9999#"，可以这样子构建前缀树，如图

const int MAXN = 2000001;
// 12代表 0~9 10个 + 1 个负号 + 1 个符号(#)
int tree[MAXN][12];
int pass[MAXN];
int cnt;
// 静态数组的方式构建
void build() {cnt = 1;
}
// 12条路进行匹配
int path(char cha) {if (cha == '#') {return 10;}else if (cha == '-') {return 11;}else {return cha - '0';}
}void insert(const string& word) {int cur = 1;pass[cur]++;for (char c : word) {int p = path(c);if (tree[cur][p] == 0) {tree[cur][p] = ++cnt;}cur = tree[cur][p];pass[cur]++;}
}int count(const string& pre) {int cur = 1;for (char c : pre) {int p = path(c);if (tree[cur][p] == 0) {return 0;}cur = tree[cur][p];}return pass[cur];
}void clear() {memset(tree, 0, sizeof(tree));memset(pass, 0, sizeof(pass));cnt = 1;
}vector<int> countConsistentKeys(vector<vector<int>>& b, vector<vector<int>>& a) {build();string builder;// for循环的作用// [3,5,20,15] --> 2#15#-5for (const auto& nums : a) {builder.clear();for (size_t i = 1; i < nums.size(); ++i) {builder += to_string(nums[i] - nums[i - 1]) + "#";}// 将2#15#-5加到前缀树中insert(builder);}// b数组也是这样的变化，每次查询收集一个答案vector<int> ans(b.size());for (size_t i = 0; i < b.size(); ++i) {builder.clear();const auto& nums = b[i];for (size_t j = 1; j < nums.size(); ++j) {builder += to_string(nums[j] - nums[j - 1]) + "#";}ans[i] = count(builder);}clear();return ans;
}

题目2：

421. 数组中两个数的最大异或值 - 力扣（LeetCode）

如何得到最大值？拿一个数字举例，为了方便，拿8为二进制举例，最高位是0，表示正数

 由于'^'是遇到与自己不相同的是0，要想得到的数字尽可能地大，那么高位尽可能地是1；那么就把每个数字转化为二进制数，每个数构造成一颗前缀树

int findMaximumXOR(const vector<int>& nums) {// 每个数字构成前缀树build(nums);// 最小值是0，自己和自己^int ans = 0;for (int num : nums) {// 找最大结果ans = max(ans, maxXor(num));}clear();return ans;
}

void build(const vector<int>& nums) {// 不需要了end和pass// 头节点cnt = 1;// 找最大值int mx = INT_MIN;for (int num : nums) {mx = max(num, mx);}// 找最大值二进制有多少个前缀0，如果所有位置前面都是0，那么没有意义，0^0还是0// 0 0 0 0 0 1 0// 0 0 0 0 1 0 0  那么前4位就没有意义，和算最大值无关// 每个位置都是从high位置插入unsigned long index;// 使用 _BitScanReverse 来找到第一个1的位置if (_BitScanReverse(&index, mx)) {high = 31 - index; // 31是int类型的位数减1}for (int num : nums) {insert(num);}
}

void insert(int num) {int cur = 1;// 从固定位置插入for (int i = high; i >= 0; --i) {// 判断当前位置i是0还是1int path = (num >> i) & 1;if (tree[cur][path] == 0) {// 如果tree数组对应位置是0，新建一条路tree[cur][path] = ++cnt;}// 不是0，就用原来的cur = tree[cur][path];}
}

int maxXor(int num) {// 使异或结果尽量大int ans = 0;// 从头结点开始int cur = 1;// high位开始for (int i = high; i >= 0; --i) {// 取第i为的状态，是0还是1int status = (num >> i) & 1;// 想要的// 1要0  0要1int want = status ^ 1;// 如果不能达成if (tree[cur][want] == 0) {// 恢复为status，被迫接受want ^= 1;}// want是真的向下走的路// (status^want) == 0 或者 1// << i 放到i位置上取// ans |= 放到ans里去ans |= (status ^ want) << i;cur = tree[cur][want];}return ans;
}