策略梯度方法【Policy Gradient】

强化学习笔记系列目录

第一章 强化学习基本概念
第二章 贝尔曼方程
第三章 贝尔曼最优方程
第四章 值迭代和策略迭代
第五章 强化学习实例分析:GridWorld
第六章 蒙特卡洛方法
第七章 Robbins-Monro算法
第八章 多臂老虎机
第九章 强化学习实例分析:CartPole
第十章 时序差分法
第十一章 值函数近似【DQN】
第十二章 基于强化学习DQN的股票预测
第十三章 策略梯度方法

---

---

本文主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程，个人觉得赵老师的课件深入浅出，很适合入门.

在上一篇文章中值函数近似【DQN】，我们介绍了用参数化的函数来近似值函数$q(s,a)$，比如DQN中用一个神经网络来表示$q(s,a)$，利用学习到的$q(s,a)$，我们可以通过贪婪的方法得到最优策略.本章我们介绍策略梯度的方法，直接用一个参数化的函数来表示策略，通过梯度上升的方法更新策略函数，最后直接得到策略${\pi }_{\theta }$.

一、参数化策略函数

函数近似的思想不仅可以应用于表示状态/动作值，也可以应用于表示策略。前面介绍的方法，如经典的值迭代、策略迭代，或者是蒙特卡洛方法和时序差分方法中，我们的策略都可以用如下的表格来表示：

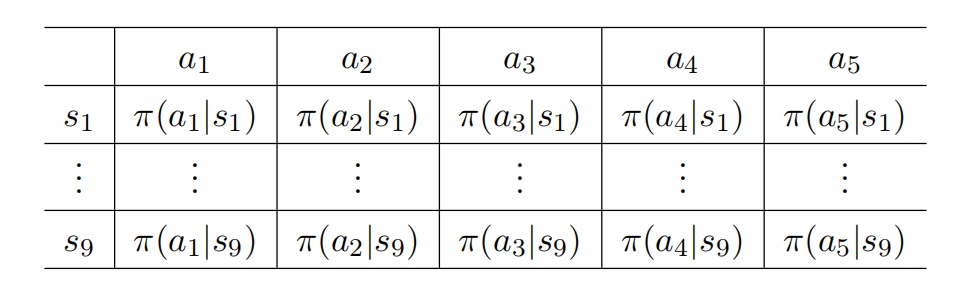
显然当状态空间和动作空间很大时，这个表格会非常大，计算所需内存会急剧上升，并且泛化能力一般。 所以同值函数的近似一样，我们也可以参数化地表示策略函数：$\pi (a|s,\theta )$，其中$\theta \in {\mathbb{R}}^m$是一个参数向量。$\pi (a|s,\theta )$也可以写为${\pi }_{\theta }(a|s)$或者$\pi (a,s,\theta )$.

如下图所示:

• 策略用一个函数来表示时，输入$s,a$，会直接输出当前状态$s$下采取动作$a$一个概率.
• 或者如右图所示，输入当前状态$s$，输出采取每个动作$a$的概率分布.

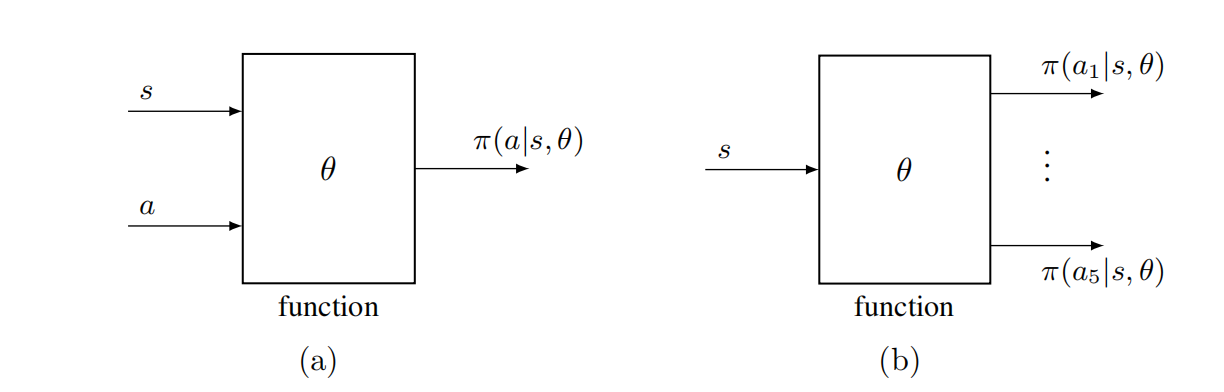
当前最有效的方法是用神经网络来近似策略函数，下面给出一个策略网络结构示意图：

通过参数化的函数来表示策略会出现一个问题，怎么衡量一个策略是不是最优策略？回顾贝尔曼最优方程的知识，我们知道，当策略用表格方法表示时，如果策略可以最大化每个状态值，则将其定义为最优策略。

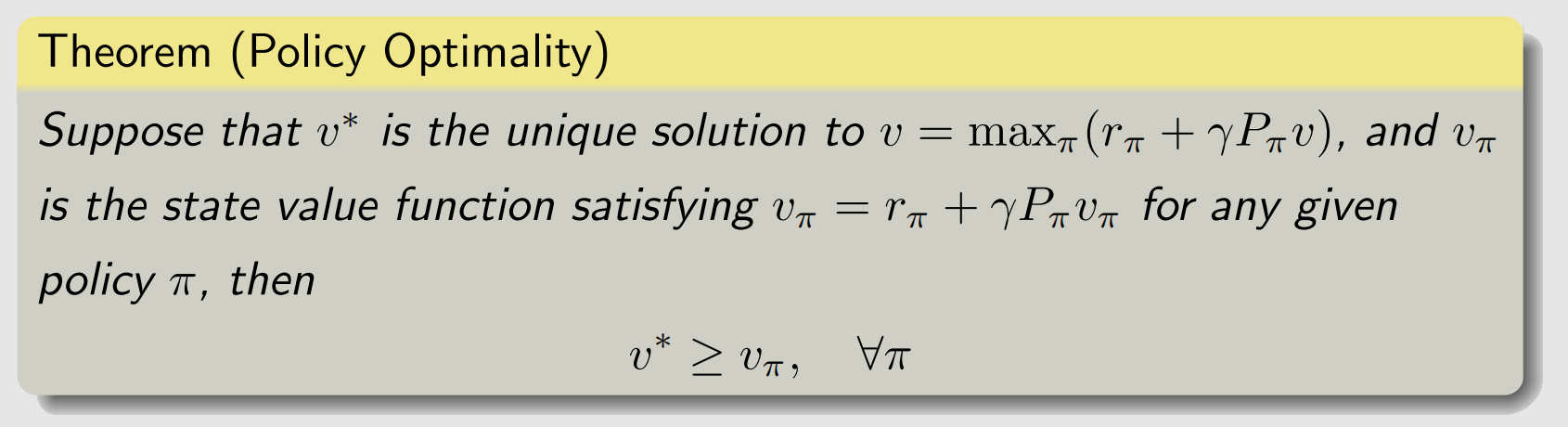
当策略用一个$\theta$的函数来表示时，如何定义最优策略呢？我们需要引入一个度量来衡量，如果某个策略能最大化这个度量，则定义其为最优策略。

二、最优策略的度量方式

（一）平均状态值

（1）定义

如果一个策略很好，那么其状态价值 $v_{\pi }(s)$ 的均值应当很大。因此可以定义度量函数为：

$$J(\theta )={\mathbb{E}}_{s\sim d}\left[v_{{\pi }_{\theta }}(s)\right],\text{\hspace{1em}(1)}$$

为什么这么定义，因为我们知道 $v_{{\pi }_{\theta }}(s)$ 依赖于当前状态和策略，因此对状态进行期望操作得到目标函数 $J(\theta )$ ，这样 $J(\theta )$ 就只依赖于策略 ${\pi }_{\theta }$ 的参数 $\theta$ ——策略越好, 则 $J(\theta )$​ 越大。 我们将对状态值函数的期望展开：
$${\bar{v}}_{\pi }\doteq {\mathbb{E}}_{s\sim d}\left[v_{{\pi }_{\theta }}(s)\right]=\sum _{s\in \mathcal{S}}d(s)v_{\pi }(s)$$

其中，$d(s)$是概率分布，也可以理解为是状态$s$的权重，${\Sigma }_{s}d(s)=1$.当我们定义出$J(\theta )$，那么策略学习可以描述为优化问题：
$$\underset{\theta }{\max }J(\theta ).$$
然后就可以利用梯度上升的方法来求最大值，从而得到最优策略${\pi }_{\theta }$.

（2）d(s)的选取

对于 $d(s)$ 怎么选取, 分为两种情况:

（一）$d$ 独立于策略 $\pi$

在这种情况下，我们特别将$d$表示为$d_0$， ${\bar{v}}_{\pi }$表示为${\bar{v}}_{\pi }^0$，以表示分布与策略无关。那么这种情况下$d_0$怎么选择呢？

• 一种情况是将所有状态认为同等重要，可以取$d_0(s)=\frac{1}{|S|},\forall s\in S$ .
• 另一种情况是当我们只对特定状态$s_0$感兴趣时（例如，Agent总是从$s_0$出发）。在这种情况下，我们可以设计
  $$d_0(s_0)=1,d_0(s\ne s_0)=0.$$

（二）$d$ 依赖于策略 $\pi$

在这种情况下，通常表示$d$为$d_{\pi }$，$d_{\pi }$是$\pi$下的一个平稳分布。平稳分布反映了给定策略下马尔可夫决策过程的长期行为。

• 如果一个状态$s$长期被频繁访问，那么它就更重要，应该得到更高的权重；
• 如果一个状态$s$很少被访问，那么它的重要性很低，应该得到较低的权重。

$d_{\pi }$的一个基本性质是它满足

$$d_{\pi }^T{P}_{\pi }=d_{\pi }^T,$$

其中$P_{\pi }$为状态转移概率矩阵。

总之，${\bar{v}}_{\pi }$是状态值的加权平均值。不同的$\theta$值会得到不同的${\bar{v}}_{\pi }$值。我们的最终目标是找到一个最优策略（或等价的最优$\theta$）来最大化${\bar{v}}_{\pi }$。上面两种不同$d(s)$的选择，主要的区别，就在于求后面梯度的时候，计算有所不同。

（3）等价形式

假设Agent通过遵循给定策略 ${\pi }_{\theta }$ 获得奖励 { R t + 1 } t = 0 ∞ \{ R_{t+1} \}_{t=0}^{\infty} {Rt+1​}t=0∞​，有时我们会看到如下的度量函数：

$$J(\theta )=\underset{n\to \infty }{\lim }\mathbb{E}\left[\sum _{t=0}^n{\gamma }^t{R}_{t+1}\right]=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{R}_{t+1}\right]\text{\hspace{1em}(2)}$$

这个度量标准乍看之下可能不容易理解，事实上，它等价于 ${\bar{v}}_{\pi }$. 由上面的公式，我们有：

$$\begin{array}{rl}\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{R}_{t+1}\right]& =\sum _{s\in \mathcal{S}}d(s)\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{R}_{t+1}|S_0=s\right]\\ & =\sum _{s\in \mathcal{S}}d(s)v_{\pi }(s)\\ & ={\bar{v}}_{\pi }.\end{array}$$

上面等式中的第一个等号是基于全概率公式，第二个等号是基于状态值函数的定义。

${\bar{v}}_{\pi }$ 也可以写成两个向量的内积。特别地，设

$$v_{\pi }={\left[\dots ,v_{\pi }(s),\dots \right]}^T\in {\mathbb{R}}^{|\mathcal{S}|},$$

$$d={\left[\dots ,d(s),\dots \right]}^T\in {\mathbb{R}}^{|\mathcal{S}|}.$$

于是，我们有

$${\bar{v}}_{\pi }=d^T{v}_{\pi }.$$

当我们分析其梯度时，该表达式将会很有用。

（二）平均奖励

（1）定义

第二种度量最优策略的目标函数为平均奖励，定义如下：
$$\begin{array}{rl}{\bar{r}}_{\pi }& \doteq \sum _{s\in \mathcal{S}}{d}_{\pi }(s)r_{\pi }(s)\\ & ={\mathbb{E}}_{S\sim d_{\pi }}\left[r_{\pi }(S)\right],\end{array}\text{\hspace{1em}(3)}$$

其中$d_{\pi }$是平稳分布，$r_{\pi }(s)$的定义如下：

$$r_{\pi }(s)\doteq \sum _{a\in \mathcal{A}}\pi (a\mid s,\theta )r(s,a)={\mathbb{E}}_{A\sim \pi (s,\theta )}[r(s,A)\mid s],$$

是对即时回报的期望。其中，$r(s,a)\doteq \mathbb{E}[R\mid s,a]={\sum }_{r}rp(r\mid s,a)$。

（2）等价形式

假设Agent通过遵循给定策略 ${\pi }_{\theta }$ 获得奖励 { R t + 1 } t = 0 ∞ \{ R_{t+1} \}_{t=0}^{\infty} {Rt+1​}t=0∞​。我们可能会在文献中看到以下常用的度量标准：

$$J(\theta )=\underset{n\to \infty }{\lim }\frac{1}{n}\mathbb{E}\left[\sum _{t=0}^{n-1}{R}_{t+1}\right].\text{\hspace{1em}(4)}$$

这个度量标准，等价于 ${\bar{r}}_{\pi }$：

$$\underset{n\to \infty }{\lim }\frac{1}{n}\mathbb{E}\left[\sum _{t=0}^{n-1}{R}_{t+1}\right]=\sum _{s\in \mathcal{S}}{d}_{\pi }(s)r_{\pi }(s)={\bar{r}}_{\pi }.$$

证明参考¹.平均奖励 ${\bar{r}}_{\pi }$ 也可以写成两个向量的内积。特别地，设
$$r_{\pi }={\left[\dots ,r_{\pi }(s),\dots \right]}^T\in {\mathbb{R}}^{|\mathcal{S}|},$$

$$d_{\pi }={\left[\dots ,d_{\pi }(s),\dots \right]}^T\in {\mathbb{R}}^{|\mathcal{S}|},$$

于是，很明显有

$${\bar{r}}_{\pi }=\sum _{s\in \mathcal{S}}{d}_{\pi }(s)r_{\pi }(s)=d_{\pi }^T{r}_{\pi }.$$

当我们推导其梯度时，该表达式将会很有用。

（三）总结

上面介绍的两种度量方式总结如下：

Note:

1. 两个度量函数都是策略$\pi$的函数，而策略又是$\theta$的函数，所以两个度量函数都是$\theta$的函数.
2. 当$\gamma <1$时，${\bar{v}}_{\pi }$和${\bar{r}}_{\pi }$是等价的，并且可以证明${\bar{r}}_{\pi }=(1-\gamma ){\bar{v}}_{\pi }$.
3. 当$\gamma =1$时，也就是公式(4).

三、策略梯度

（一）策略梯度定理

通过上面的介绍，我们知道，当定义出$J(\theta )$后，剩下的问题就是求解下面的优化问题：
$$\underset{\theta }{\max }J(\theta ).\text{\hspace{1em}(5)}$$
一个很自然的想法就是用梯度上升法来做：
$${\theta }_{t+1}={\theta }_t+\alpha \nabla J({\theta }_t)\text{\hspace{1em}(6)}$$
所以一个关键的问题是$J(\theta )$的梯度怎么求？下面给出策略梯度定理.

定理【策略梯度定理】

$J(\theta )$ 的梯度为
$${\nabla }_{\theta }J(\theta )=\sum _{s\in S}\eta (s)\sum _{a\in A}{\nabla }_{\theta }\pi (a|s,\theta )q_{\pi }(s,a),\text{\hspace{1em}(7)}$$
其中，$\eta$ 是状态分布函数，${\nabla }_{\theta }\pi$ 是$\pi$关于 $\theta$ 的梯度。此外，上式可以通过期望的形式简化为：
$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{S\sim \eta ,A\sim \pi (S,\theta )}\left[{\nabla }_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)\right],\text{\hspace{1em}(8)}$$
其中 $\ln$ 表示自然对数。

其中：

• $J(\theta )$ 可以是 ${\bar{v}}_{\pi }$、${\bar{r}}_{\pi }$ 或 ${\bar{v}}_{\pi }^0$
  • 也就是说$J(\theta )$取不同值，会导出不同的梯度表达式;
  • $\eta (s)$取法不同，也会导致梯度不一样.
• “$=$” 可能表示严格相等、近似相等或成比例，这个取决于$\gamma$的取值.
• 所以在导出更具体的形式时，需要对上面几种情况进行区分，（7）和（8）是策略梯度的统一形式.

写成式(8)这种期望形式很有用，因为在进行梯度上升算法的过程中，我们可以用一个采样来替代期望（随机梯度下降原理）。那么为什么式 (7) 可以表示为式 (8)?证明如下。根据期望的定义，(7) 可以重写为
$${\nabla }_{\theta }J(\theta )=\sum _{s\in S}\eta (s)\sum _{a\in A}{\nabla }_{\theta }\pi (a|s,\theta )q_{\pi }(s,a)={\mathbb{E}}_{S\sim \eta }\left[\sum _{a\in A}{\nabla }_{\theta }\pi (a|S,\theta )q_{\pi }(S,a)\right].\text{\hspace{1em}(9)}$$

我们知道$\ln \pi (a|s,\theta )$ 的梯度为
$${\nabla }_{\theta }\ln \pi (a|s,\theta )=\frac{{\nabla }_{\theta }\pi (a|s,\theta )}{\pi (a|s,\theta )},$$

因此
$${\nabla }_{\theta }\pi (a|s,\theta )=\pi (a|s,\theta ){\nabla }_{\theta }\ln \pi (a|s,\theta ).\text{\hspace{1em}(10)}$$

将 (10) 代入 (9) 得
$${\nabla }_{\theta }J(\theta )=\mathbb{E}\left[\sum _{a\in A}\pi (a|S,\theta ){\nabla }_{\theta }\ln \pi (a|S,\theta )q_{\pi }(S,a)\right]={\mathbb{E}}_{S\sim \eta ,A\sim \pi (S,\theta )}\left[{\nabla }_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)\right].$$

值得注意的是，为了确保 $\ln \pi (a|s,\theta )$ 有效，对于所有 $(s,a)$，$\pi (a|s,\theta )$ 必须为正。这可以通过 softmax 函数来实现：
$$\pi (a|s,\theta )=\frac{e^{h(s,a,\theta )}}{{\sum }_{a^{\prime }\in A}{e}^{h(s,a^{\prime },\theta )}},a\in A,\text{\hspace{1em}(11)}$$
其中 $h(s,a,\theta )$ 是指示在状态 $s$ 下选择动作 $a$ 的偏好函数。

• 式 (11) 中的策略满足 $\pi (a|s,\theta )\in [0,1]$，且对于任意 $s\in S$，${\sum }_{a\in A}\pi (a|s,\theta )=1$.
• 这种策略函数可以通过神经网络实现。网络的输入为 $s$，输出层为一个 softmax 层，因此网络对所有 $a$ 输出 $\pi (a|s,\theta )$，且输出的和为 1.

由于 $\pi (a|s,\theta )>0$ 对所有 $a$ 成立，因此该策略是随机的，具有探索性。策略并不直接告诉采取哪一个动作，而是根据策略的概率分布来选择动作。

（二）Discount case 结论

接下来我们将给出有折扣因子情况下度量函数的梯度，其中 $\gamma \in (0,1)$。有折扣因子情况下，状态值和动作值定义为
$$v_{\pi }(s)=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots \mid S_t=s],$$

$$q_{\pi }(s,a)=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots \mid S_t=s,A_t=a].$$

有 $v_{\pi }(s)={\sum }_{a\in A}\pi (a|s,\theta )q_{\pi }(s,a)$，并且状态值满足Bellman方程。首先，我们证明 ${\bar{v}}_{\pi }(\theta )$ 和 ${\bar{r}}_{\pi }(\theta )$ 是等价的度量。

引理 1【${\bar{v}}_{\pi }(\theta )$ 和 ${\bar{r}}_{\pi }(\theta )$ 之间的等价性】。

在有折扣因子情况下，当 $\gamma \in (0,1)$ 时，有
$${\bar{r}}_{\pi }=(1-\gamma ){\bar{v}}_{\pi }.\text{\hspace{1em}(12)}$$

证明：注意 ${\bar{v}}_{\pi }(\theta )=d_{\pi }^T{v}_{\pi }$ 和 ${\bar{r}}_{\pi }(\theta )=d_{\pi }^T{r}_{\pi }$，其中 $v_{\pi }$ 和 $r_{\pi }$ 满足Bellman方程 $v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$。在Bellman方程两边乘以 $d_{\pi }^T$ 得
$${\bar{v}}_{\pi }={\bar{r}}_{\pi }+\gamma d_{\pi }^T{P}_{\pi }{v}_{\pi }={\bar{r}}_{\pi }+\gamma d_{\pi }^T{v}_{\pi }={\bar{r}}_{\pi }+\gamma {\bar{v}}_{\pi },$$
注意前面提到$d(s)$有一个性质$d_{\pi }^T{P}_{\pi }=d_{\pi }^T$.

其次，下面的引理给出了任何 $s$ 下 $v_{\pi }(s)$ 的梯度，详细证明见¹的第9章.

引理 2【$v_{\pi }(s)$ 的梯度】

在有折扣因子情况下，对于任何 $s\in S$，有
$${\nabla }_{\theta }{v}_{\pi }(s)=\sum _{s^{\prime }\in S}{\mathrm{Pr}}_{\pi }(s^{\prime }|s)\sum _{a\in A}{\nabla }_{\theta }\pi (a|s^{\prime },\theta )q_{\pi }(s^{\prime },a),\text{\hspace{1em}(13)}$$
其中
$${\mathrm{Pr}}_{\pi }(s^{\prime }|s)\doteq \sum _{k=0}^{\infty }{\gamma }^k[P_{\pi }^k{]}_{s{s}^{\prime }}=[(I_n-\gamma P_{\pi }{)}^{-1}{]}_{s{s}^{\prime }}$$
是在策略 $\pi$ 下从 $s$ 转移到 $s^{\prime }$ 的折扣总概率。这里，$[\cdot {]}_{s{s}^{\prime }}$ 表示矩阵中第 $s$ 行和第 $s^{\prime }$ 列的元素，$[P_{\pi }^k{]}_{s{s}^{\prime }}$ 是在策略 $\pi$ 下从 $s$ 到 $s^{\prime }$ 用 $k$ 步转移的概率。

由上面两个引理，我们可以导出两个定理，也就是两种不同情况下$J(\theta )$的梯度，详细证明见¹的第9章.

定理 2【折扣情况下 ${\bar{v}}_{\pi }^0$ 的梯度】

在折扣因子 $\gamma \in (0,1)$ 的情况下，${\bar{v}}_{\pi }^0$ 的梯度 $d_0^T{v}_{\pi }$ 为
$$\begin{array}{rl}{\nabla }_{\theta }{\bar{v}}_{\pi }^0& =\mathbb{E}\left[{\nabla }_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)\right]\\ & =\sum _{s\in S}{\rho }_{\pi }(s)\sum _{a\in A}\pi (a|s,\theta ){\nabla }_{\theta }\ln \pi (a|s,\theta )q_{\pi }(s,a).\end{array}$$
其中 $S\sim {\rho }_{\pi }$ 且 $A\sim \pi (A|S,\theta )$。这里，状态分布 ${\rho }_{\pi }$ 为
$${\rho }_{\pi }(s)=\sum _{s^{\prime }\in \mathcal{S}}{d}_0(s^{\prime }){\mathrm{Pr}}_{\pi }(s|s^{\prime }),s\in \mathcal{S},$$
其中
$${\mathrm{Pr}}_{\pi }(s|s^{\prime })=\sum _{k=0}^{\infty }{\gamma }^k{\left[P_{\pi }^k\right]}_{s^{\prime }/s}={\left[(I-\gamma P_{\pi }{)}^{-1}\right]}_{s^{\prime }/s}$$
为在策略 $\pi$ 下，从状态 $s^{\prime }$ 以折扣概率转移至状态 $s$ 的总概率。

定理 3【折扣情况下 ${\bar{r}}_{\pi }$ 和 ${\bar{v}}_{\pi }$ 的梯度】

在折扣因子 $\gamma \in (0,1)$ 的情况下，${\bar{r}}_{\pi }$ 和 ${\bar{v}}_{\pi }$ 的梯度为
$${\nabla }_{\theta }{\bar{r}}_{\pi }=(1-\gamma ){\nabla }_{\theta }{\bar{v}}_{\pi }\approx \sum _{s\in \mathcal{S}}{d}_{\pi }(s)\sum _{a\in \mathcal{A}}{\nabla }_{\theta }\pi (a|s,\theta )q_{\pi }(s,a)$$

$$=\mathbb{E}\left[{\nabla }_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)\right],$$

其中 $S\sim d_{\pi }$ 且 $A\sim \pi (A|S,\theta )$。当 $\gamma$ 趋近于 1 时，此近似更为精确。

（三）Undiscount Case 结论

也就是$\gamma =1$时的情况，我们考虑公式(4)的梯度，也就是
$$J(\theta )=\underset{n\to \infty }{\lim }\frac{1}{n}\mathbb{E}\left[\sum _{t=0}^{n-1}{R}_{t+1}\right]={\bar{r}}_{\pi }.$$
下面直接给出${\bar{r}}_{\pi }$的梯度，具体证明参考¹的第9章.

定理 4【非折扣情况下 ${\bar{r}}_{\pi }$ 的梯度】

在非折扣情况下，平均奖励 ${\bar{r}}_{\pi }$ 的梯度为
$${\nabla }_{\theta }{\bar{r}}_{\pi }=\sum _{s\in \mathcal{S}}{d}_{\pi }(s)\sum _{a\in \mathcal{A}}{\nabla }_{\theta }\pi (a|s,\theta )q_{\pi }(s,a)$$

$$=\mathbb{E}\left[{\nabla }_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)\right],$$

其中 $S\sim d_{\pi }$ 且 $A\sim \pi (S,\theta )$。相比于定理 3中的折扣情况，非折扣情况下 ${\bar{r}}_{\pi }$ 的梯度更为简洁，因为上式严格成立，且 $S$ 满足平稳分布。

总的来说，定理2,3,4是定理1在不同情况下的具体版本.

四、REINFORCE

上一小节我们介绍了如何计算$J(\theta )$的梯度，我们接下来展示如何使用基于梯度的方法来优化度量函数，以获得最优策略。用于最大化 $J(\theta )$ 的梯度上升算法为

$$\begin{array}{rl}{\theta }_{t+1}& ={\theta }_t+\alpha {\nabla }_{\theta }J({\theta }_t)\\ & ={\theta }_t+\alpha \mathbb{E}\left[{\nabla }_{\theta }\ln \pi (A|S,{\theta }_t)q_{\pi }(S,A)\right],\end{array}$$
其中 $\alpha >0$ 是一个常数学习率。由于上式中的真实梯度未知（期望不好求），我们可以用随机梯度替代真实梯度，以获得以下算法：
$${\theta }_{t+1}={\theta }_t+\alpha {\nabla }_{\theta }\ln \pi (a_t|s_t,{\theta }_t)q_t(s_t,a_t),$$
其中 $q_t(s_t,a_t)$ 是 $q_{\pi }(s_t,a_t)$ 的一个近似值。$q_t(s_t,a_t)$主要有两种方法得到：

1. 蒙特卡洛估计；
2. TD 方法.

如果 $q_t(s_t,a_t)$ 是通过蒙特卡罗估计得到的，那么该算法称为 REINFORCE或蒙特卡罗策略梯度，这是最早且最简单的策略梯度算法之一。REINFORCE算法的伪代码如下：

核心思想就是:

• 利用累计奖励值$G_t$作为$q_t(s_t,a_t)$的无偏采样，然后再根据这个采样更新策略函数的参数$\theta$.
• ${\nabla }_{\theta }\ln \pi (a_t|s_t,{\theta }_t)$的计算是比较方便的，比如策略函数是一个神经网络，那么在Pytorch里，我们可以根据输出，通过反向传播自动计算梯度.

下图所示为REINFORCE 算法示意:

1. 首先我们需要一个策略模型${\pi }_{\theta }$来与环境进行交互
   • 首先从初始状态$s_0$输出动作概率，输出动作概率后，通过 sample() 函数得到一个具体的动作$a_0$，与环境交互后，得到一个奖励$r_1$，并转移到新的状态$s_1$……
   • 循环直到整个episode结束，我们可以得到整个回合的数据。
2. 得到回合数据之后，我们再去执行 learn() 函数，在 learn() 函数里 面，我们就可以用这些数据去构造损失函数，“扔”给优化器优化，更新我们的策略模型，也就是更新参数$\theta$。

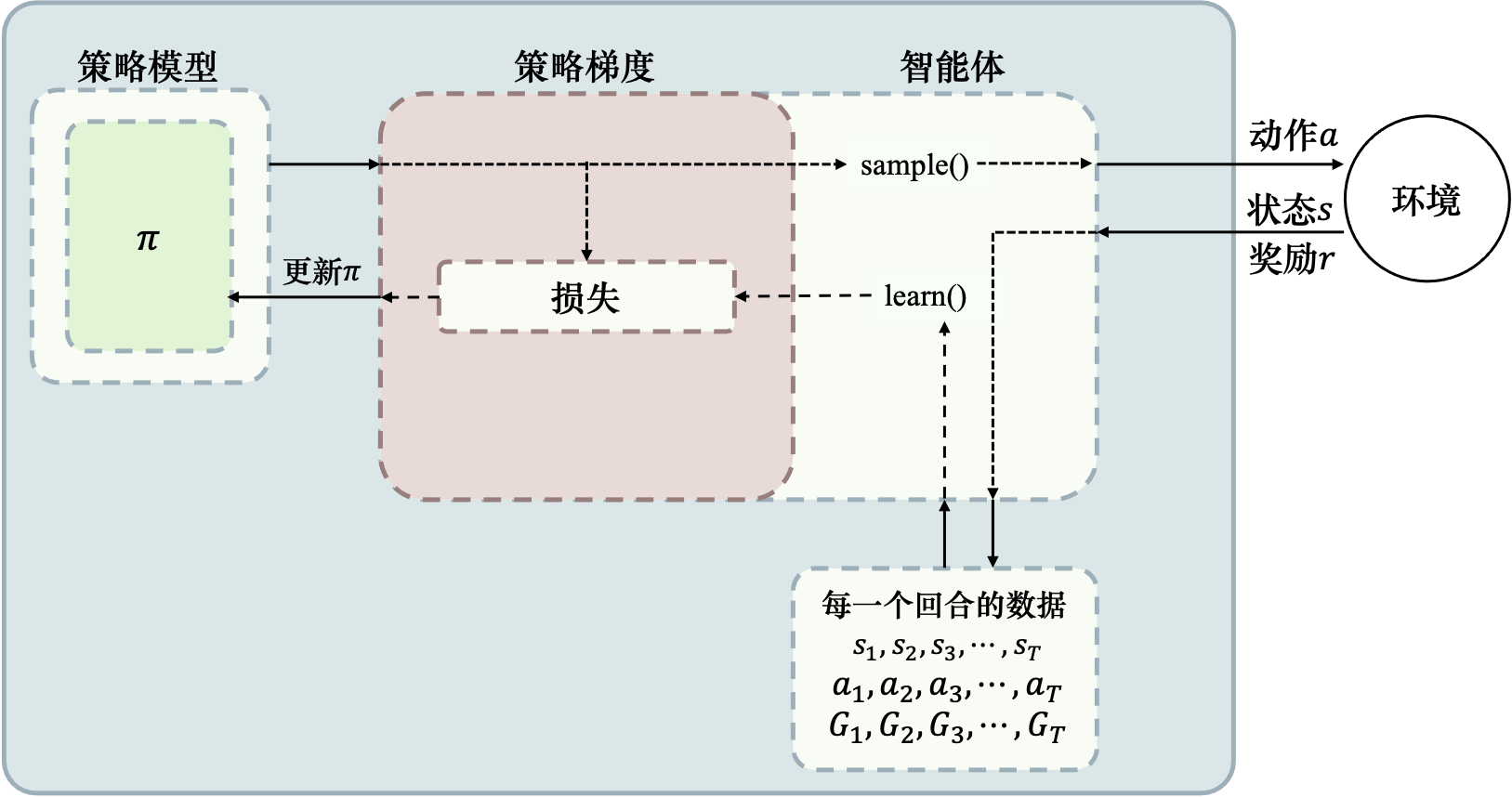
因为REINFORCE是基于蒙特卡洛采样，在蒙特卡洛方法文章里，我们也指出了蒙特卡洛方法的一些缺点，所以REINFORCE也有一些相同的问题：

1. 适用于Episodic任务
   • 通常情况下，任务需要有终止状态，REINFORCE才能直接计算累积折扣奖励
2. 低数据利用效率
   • 实际中，REINFORCE需要大量的训练数据
3. 高训练方差
   • 从单个或多个Episode采样得到的值函数具有很高的方差
   • 下一章我们会介绍如何引入基线函数来降低样本方差

参考资料

---

1. Zhao, S… Mathematical Foundations of Reinforcement Learning. Springer Nature Press and Tsinghua University Press. ↩︎ ↩︎ ↩︎ ↩︎