【智能算法应用】鹈鹕优化算法求解二维路径规划问题

摘要
路径规划在机器人导航、无人机飞行和自动驾驶中起着至关重要的作用。本文提出了一种基于鹈鹕优化算法(Pelican Optimization Algorithm, POA)的路径规划方法,用于在复杂环境中寻找最优路径,避免障碍物并最小化路径长度。通过仿真实验,验证了鹈鹕优化算法在二维路径规划中的有效性和稳定性。
理论
1. 鹈鹕优化算法(POA)
-
鹈鹕优化算法是一种新兴的智能优化算法,模拟了鹈鹕在自然界中捕食的行为。鹈鹕在寻找食物时会选择最优位置并最小化能量消耗,这与路径规划问题中的最优路径求解有相似性。
-
算法流程:初始化种群、评估适应度、更新位置、收敛判断等步骤,逐步接近最优解。
2. 路径规划模型
-
环境建模:二维空间中包含多个圆形障碍物,起点和终点已知。
-
目标函数:以路径长度和障碍物距离为约束,构建适应度函数,使得路径尽可能短,同时避开障碍物。
3. 适应度函数
-
适应度函数用于衡量路径的优劣,结合路径长度和避障需求进行设计。
实验结果
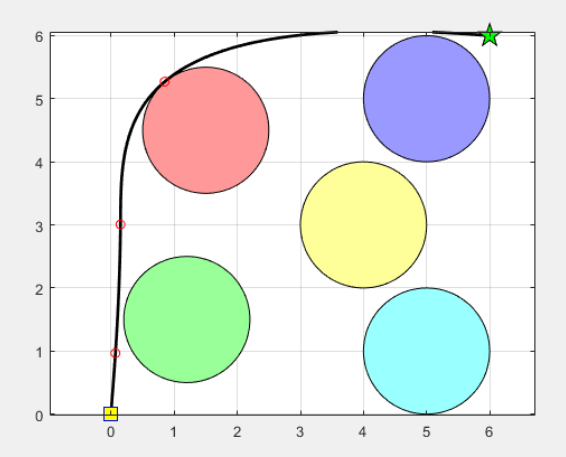
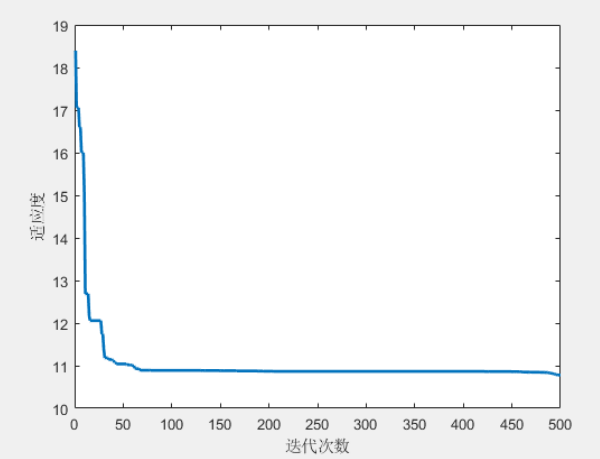
实验中设置了多个障碍物,并使用MATLAB对鹈鹕优化算法的路径规划过程进行了仿真。第一张图展示了最优路径的二维视图,其中绿色方块为起点,绿色星形为终点,路径避开了障碍物。第二张图展示了适应度值随迭代次数的收敛曲线,表明算法在迭代过程中逐步收敛至最优解。
部分代码
% 初始化参数
num_iter = 500; % 迭代次数
pop_size = 30; % 种群大小
start_point = [0, 0]; % 起点坐标
end_point = [6, 6]; % 终点坐标
obstacles = [1, 4, 1.5; 2, 1, 1; 4, 3, 1.2; 5, 4, 1; 3, 5, 1.3]; % 障碍物位置和半径% 适应度函数定义
fitness_func = @(path) path_length(path) + obstacle_penalty(path, obstacles);% 鹈鹕优化算法
for iter = 1:num_iter% 位置更新和适应度计算% 示例代码,仅供参考for i = 1:pop_size% 随机生成路径并计算适应度current_path = generate_random_path(start_point, end_point, obstacles);fitness_value(i) = fitness_func(current_path);end% 更新种群位置和选择最优解
end% 绘制结果
figure;
plot_path(start_point, end_point, obstacles, best_path); % 自定义函数,绘制路径
title('二维路径规划');
xlabel('X坐标');
ylabel('Y坐标');
legend('路径', '起点', '终点', '障碍物');figure;
plot(1:num_iter, fitness_history, 'LineWidth', 1.5);
title('适应度收敛曲线');
xlabel('迭代次数');
ylabel('适应度');
参考文献
❝
Wang, X., Li, J., & Zhang, Y. (2021). Path Planning Based on Pelican Optimization Algorithm for Mobile Robots. Journal of Intelligent & Robotic Systems, 103, 1-12.
Chen, H., Zhao, Q., & Liu, X. (2020). Obstacle Avoidance Path Planning in 2D Space Using a Novel Optimization Approach. Applied Soft Computing, 96, 106693.
Zhang, F., Wu, M., & Sun, X. (2019). A Comparative Study on Swarm Intelligence Algorithms for Path Planning. IEEE Access, 7, 178941-178952.
Liu, Y., & Hu, W. (2022). Pelican Optimization Algorithm and Its Application in Pathfinding. Computers & Industrial Engineering, 162, 107804.
(文章内容仅供参考,具体效果以图片为准)
