金蝶云苍穹的Extension与Nop平台的Delta的区别

最近有同学介绍我看一篇金蝶云苍穹的文章，都1202年了，听说还有人不知道扩展与继承的区别，这其中介绍了一个有别于传统继承概念的所谓 扩展(Extension)概念。这个概念也不是云苍穹原创的，在odoo框架中就存在类似的做法，参见继承和扩展。一个有趣的问题是，Nop平台中的x:extends运算和云苍穹的扩展是同一个概念吗？答案是：并不是同一个概念，扩展只是一种AdHoc式的针对具体问题的不完整的解决方案，而Nop平台中的Delta合并，则是更高层面的抽象，它在数学层面上定义了完备的数学运算机制，相当于是引入了一种标准化的、新的底层语法结构。

一. 继承与扩展的区别

在云苍穹的定义中

扩展与继承统称为扩展开发，是金蝶云苍穹提供的对已有实体进行个性化开发时采取的开发模式。

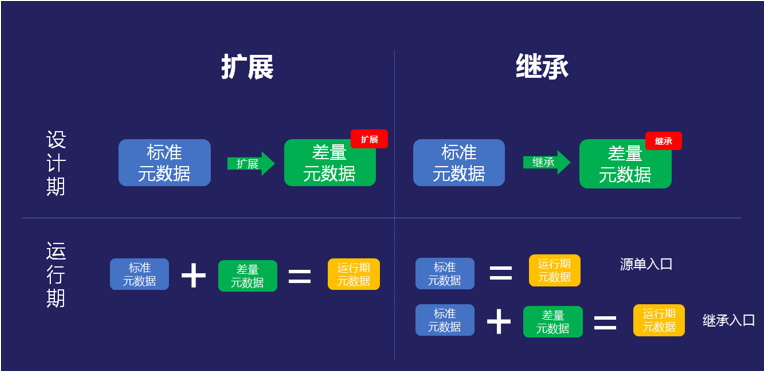
从云苍穹的文章中可以看出，他们已经明确意识到了扩展本质上是一种差量数据（Delta)。继承在抽象层面上是标准结构结合差量结构产生一个新的结构。也就是说，继承是保持原有的结构和原有的实体名不变，但是增加了一个新的实体名和新的实体结构。

ClassB = ClassA + Delta

而扩展是结合差量结构后直接替换原有的结构。也就是说，保持实体的名不变，这样所有使用到该实体的地方都会自动使用扩展后的实体结构。

ClassA <- ClassA + Delta

二. Delta差量与Extension扩展的区别

可逆计算理论是我于2007年左右提出的支持面向语言编程范式（Language Oriented Programming）的下一代软件构造理论，它在数学层面定义了一整套严谨的Delta差量运算机制，并通过XLang程序语言将它们固化为具体的程序语法结构。可逆计算理论中的Delta差量是真正原创的概念，它的思想来源是物理学和数学中的微分动力系统、微扰论、熵增原理、群论等基础理论，与软件工程领域已有的扩展概念并没有直接关系。

关于可逆计算理论的介绍，参见可逆计算：下一代软件构造理论和可逆计算理论中的可逆到底指的是什么？。

与可逆计算理论中的Delta概念相比，扩展可以看作是一种基于程序员经验总结的、面向特定应用场景的、AdHoc式的一种具体解决方案，而Delta则是一种系统化的、数学层面上具有严谨定义的、应用范围更广的一种通用软件构造原理（Docker技术就可以看作是可逆计算的一个具体实例）。具体来说，有如下区别

2.1 云苍穹的扩展只针对少数具体的模型

云苍穹中的扩展主要应用于实体模型和视图模型等少数固定模型，而且为了支持扩展概念，需要在实体模型引擎和视图模型引擎中增加相应的实现代码。也就是说，它是针对少数几个特定模型特殊设计和开发的机制。针对每一个模型，具体的差量内容和差量合并规则都需要特殊编码去实现。换句话说，并没有统一的差量结构定义规则和差量结构合并规则，云苍穹是在具体的模型层面针对每一个模型去定义对应的扩展机制。

EntityModelA <-MergerForEntityModel(EntityModelA, DeltaForEntityModel)

ViewModelA <- MergerForViewModel(ViewModelA, DeltaForViewModel)

具体实现过程大概是，先解析得到EntityModel对象，然后再应用某个EntityModelMerger来合并EntityModel和DeltaForEntityModel。具体的合并算法针对不同的模型需要单独进行编制。

可逆计算中的Delta差量合并是在模型层之下的统一的结构层完成，与具体的模型无关，合并规则由xdef元模型来规定。

XNode = Loader(virtualPath)

Model = Parser(XNode)

Nop平台中我们是通过虚拟文件系统来统一管理模型文件，然后使用统一的XNode加载器解析得到通用的XNode节点，在这个过程中会实现Delta合并算法。得到XNode之后我们再解析XNode得到具体的模型。也就是说，并不是EntityModel = EntityModel + Delta，而是XNode = XNode + Delta, EntityModel = Parser(XNode)。Delta差量合并不是作用于具体的模型层面，而是作用于元模型约束下的XNode统一结构层面。

所有的数学定理只要证明一次，世界上所有其他人就不要证明了。类似的，Delta的运算规律只要在Nop平台中定义一次，所有的模型（包括现在和未来可能的模型）就都不需要实现了。相比于云苍穹的扩展概念，Delta差量是在更高的抽象层面上定义，它与扩展是本质上不同的做法。

具体XNode合并算法的介绍，参见XDSL：通用的领域特定语言设计和通用的Delta差量化机制

2.2 Delta差量合并作用于Tree结构并且包含删除语义

传统的继承和扩展本质上都是基于类结构的，而类是一个两级结构：类名+成员列表。在一个类中，我们通过方法名和属性名定位到具体的某一个方法或者属性。如果从结构层面看，类就相当于是一个Map结构，类的继承和扩展在结构层面上可以被理解为Map的覆盖合并。

Map = Map extends Map

如果有一个属性具有内部结构，比如它是一个对象或者一个列表，那么一般的类扩展只会整体覆盖该属性，并没有一种合适的方法来定位到属性内部的某个条目或者子属性。

可逆计算理论中明确引入了领域坐标系的概念，强调每一个语法节点都具有唯一的可用于定位的领域坐标，如果采用分层坐标，很自然的就构成一个树结构。树结构中，从根节点到当前节点的路径就是这个节点的一种绝对坐标，节点在父节点中的名称可以看作是它在父节点范围内的相对坐标。Delta差量合并定义在树结构上而不是Map结构上

Tree = Tree x-extends Tree

在使用XML存储形式时，我们为XML节点引入了特殊约定的x:extends属性

<orm x:schema="/nop/schema/orm/orm.xdef"x:extends="base.orm.xml"><x:post-extends><orm-gen:JsonComponentSupport xpl:lib="/nop/orm/xlib/orm-gen.xlib"/></x:post-extends><entities><entity name="xxx.MyEntity"><columns><column name="jsonExt" code="JSON_EXT" propId="101" tagSet="json"                           stdSqlType="VARCHAR"precision="4000"/><column name="status" x:override="remove" /></columns><!-- 最终会自动生成component配置<components><component name="jsonExtComponent"class="io.nop.orm.component.JsonOrmComponent"><prop name="jsonText" column="jsonExt" /></component></components>--></entity></entities>
</orm> 

通过x:extends可以继承已有的Tree结构，然后可以任意定制这个复杂嵌套的Tree结构中的任意一个节点上任意属性。从根节点向下进行合并时，如果是集合节点，要求这个集合元素必须具有name/id这种可以用于唯一定位的标识属性。

Delta差量合并提供了删除语义，例如上面的例子中x:override="remove"表示删除本节点。传统的继承、扩展等机制一般都没有提供真正的删除语义，大部分是新增语义，修改语义都很少。但是可逆计算是面向程序结构长期演化的软件构造理论，演化一定是要允许破坏已有结构的，所以它必然包含删除和更新语义。

除了两个静态Tree结构之间的合并运算之外，可逆计算理论的完整形式需要引入动态Generator。

App = Delta x-extends Generator<DSL>

反映到结构层面就是

Tree = Tree x-extends Tree<Tree>

整个应用程序可以用一个Tree来表达（源码目录树+源码内部的抽象语法树），Delta本身也可以用Tree表达。Generator本质上就是一段代码，可以用抽象语法树(Abstract Syntax Tree)来表达，而DSL领域特定语言同样是使用AST来表达。

在上面的例子中，x:post-extends就是一种动态生成机制，它可以动态生成base节点用于Delta合并。

2.3 完整的关于Delta差量的理论

云苍穹的扩展概念虽然提到了差量，但是对于差量的理解局限于浅层的常识层面，而可逆计算理论中的Delta差量则接近于数学中群(Group)的概念，在概念的一致性和完备性方面远远超过扩展。关于群和Delta差量的关系，可以参见写给程序员的差量概念辨析,以Git和Docker为例。

首先，根据 A = 0 + A，任何全量都是差量的特例，我们完全可以采用同样的形式来表达差量和全量，没有必要为差量单独定义一个特殊的形式。如果差量和全量采用同样的形式，那么一个必然的推论就是差量的差量也是一个普通的差量，我们可以引入更丰富的差量应用模式。

第二，可逆计算中的差量满足结合律，我们可以利用它定义独立于Base的差量合并运算，实现差量的独立管理。换句话说，在不知道应用到哪个Base之前，我们就可以将多个Delta合并在一起构成一个新的Delta。

A = (B+Delta1) + Delta2 = B + (Delta1 + Delta2)

第三， 可逆计算中的差量独立于Base存在，同一个差量可以作用于多个不同的Base。

A = A1 + Delta,  B = B1 + Delta

利用这一点，我们可以开发出新的软件复用模式。比如通过一个工作流的Delta来为任意实体引入工作流支持等。
在Nop平台中，我们将元编程和Delta差量结合在一起，实现了大量传统软件工程中无法想象的高阶复用模式。而且它们全部在编译期完成，对运行期性能没有任何影响，也不会把复杂性带到运行时。

更多介绍参见写给程序员的可逆计算理论辨析和写给程序员的可逆计算理论辨析补遗

2.4 多个Delta分支

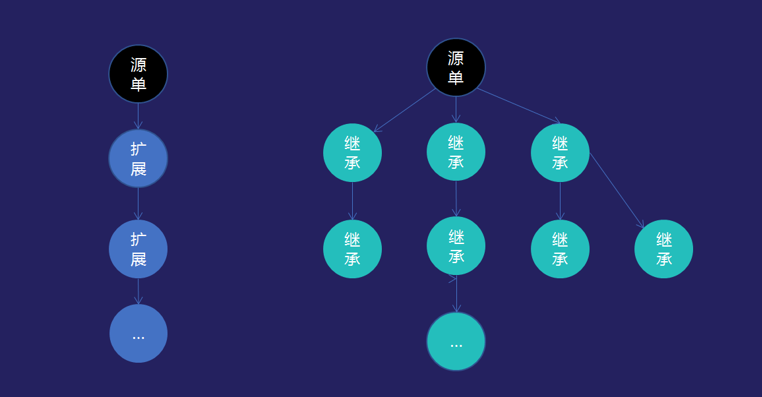
在云苍穹的文章中，提到扩展和继承的一个区别是"一个单只能扩展一次，但是可以对扩展之后的单再次扩展。而一个单可以继承多次，继承后的单也可以继续继承多次"。也就是如上图所示，扩展只能形成唯一的扩展链，而继承则可以形成多个不同的继承链。但是在可逆计算理论中，Delta差量并不存在这种限制。在Nop平台的具体实现中，我们可以通过给Delta赋予不同的名字，从而允许存在多条Delta扩展链。例如

/_delta/hunan/abc
/_delta/anhui/abc
/_delta/product/abc
/abc

上面的示例中，/_delta/hunan/abc表示在deltaId=hunan的Delta层中定义了abc这个文件，而/_delta/product/abc则表示在deltaId=product的Delta层中定义了abc这个文件。
在/_delta/hunan/abc文件中，我们可以通过x:extends="super"来表示继承上一层的内容，如果没有设置x:extends属性，则表示当前文件会覆盖上一层的文件，而不是实现两者的合并。

在配置文件中，我们可以通过nop.core.vfs.delta-layer-ids=hunan,product来控制如何实现多个Delta层之间的堆叠。也就是说，利用这种额外的装配机制，我们可以突破云苍穹中只允许单一扩展链的限制。

三. 可逆计算的具体实现

虽然不知道云苍穹的扩展机制的具体实现，但如果要在模型层实现，必然会导致大量冗余的代码，还很容易产生各种潜在的不一致性。在Nop平台中，实现差量运算和动态差量生成只需要数千行代码（不考虑XScript脚本语言自身的实现，本质上也可以利用现有的脚本语言引擎，但是会缺少一些方便的元编程机制），而且所有的可逆计算支持可以被封装在统一的模型加载器抽象之下。也就是说，只要将普通Java工程中常用的JsonReader.readJson(classPath)调用替换成Nop平台的ResourceComponentManager.instance().loadComponentModel(virtualPath)我们就可以立刻获得差量合并、动态模型生成、模型解析缓存、模型依赖追踪等一系列差量运算支持机制。同时可以自动获得多租户支持，每个租户都可以具有自己不同的Delta差量定义。设计原理的介绍参见从张量积看低代码平台的设计

基于可逆计算理论设计的低代码平台NopPlatform已开源：

• gitee: canonical-entropy/nop-entropy
• github: entropy-cloud/nop-entropy
• 开发示例：docs/tutorial/tutorial.md
• 可逆计算原理和Nop平台介绍及答疑_哔哩哔哩_bilibili