递归专题BFS

目录

介绍以及认识

汉诺塔问题

题目解析

思路

合并两个有序的链表

思路

代码实现

翻转链表

 思路

代码实现

两两交换链表中的节点

思路 

代码实现 

快速幂

思路

代码实现

---

介绍以及认识

先来说一下有关递归的几个算法;深度优先搜索,深度优先遍历,广度优先搜索,广度优先遍历以及回溯,剪枝,记忆化搜索;

我们一说到递归,内心就会不自觉的产生恐惧,因为递归式连续多层嵌套函数,整个过程线是很长的,是抽象的,正常人是想不到那么深的,所以我们要想学会使用递归,就需要先克服对递归的恐惧;

递归的实质其实就是重复的做同样的事情;

第一步,知己知彼;

我们需要先了解清楚上面我说的几种算法究竟是什么;
深度优先搜索(BFS):可以使用DFS的标志一般是决策树,二叉树,单支树等;这个算法其实还是暴力枚举,只不过是使用递归简化了代码;他的时间复杂度仍然是很大,一般对速度有要求的题,使用DFS就会溢出;
深度优先遍历其实就是DFS,他俩是一样的,DFS的形式就是遍历,而目的就是搜索;

广度优先遍历(BFS):广度优先遍历的核心在于层序遍历;其遍历可以形象化为"水波扩散";需要借助队列实现,小技巧是使用向量数组;难度相比DFS较小;BFS并不是暴力枚举,所以时间复杂度要优于DFS;
同样的广度优先遍历也是BFS,形式是遍历,目的是搜索;

回溯:回溯通常在DFS中出现;顾名思义就是回来的意思,如果见到有的题解有回溯和DFS,我们可以认为回溯其实就是DFS;

剪枝:在DFS的多种情况中,当我们已经确定某一种情况得不到正确结果,那么我们就把这条路径剪掉,不再继续遍历;就是截断的意思;

记忆化搜索:就是在DFS中加上了个备忘录;因为在不同的情况中可能会调用相同的DFS函数,将数据储存起来就会减少堆栈压力,从而提高代码效率;

第二步,信任(相信我的递归黑盒子可以帮我完成任务)

1.不要特别的在意递归的每个过程细节,我们只要宏观的把他当做一个黑盒子;
2.相信这个黑盒子会帮我处理好后面的事情;
3.做好当前函数这个层的任务即可;

不明白什么意思?
举个例子:我现在要使用DFS递归打印0~n的数;

#include<iostream>
using namespace std;void dfs(int cur_num,int n)
{if (n == cur_num){cout << cur_num << " ";return;}cout << cur_num << " ";dfs(cur_num + 1, n);        
}int main()
{int n; cin >> n;dfs(0,n);return 0;
}

我们要从0到打印到n,那么是不是需要一个起点参数和一个终点参数(这里的参数是根据题目自行考虑),此时这个DFS的意思就是"打印cur_num到n的数";对吧;

我们在函数中调用了一个dfs(0,n);这时候就好像是下达了一个命令"你给我打印从0到n",然后函数开始执行,那么重点来了;递归就是自己调用自己;说明DFS中里面肯定还要调用DFS,对吧;这时候在结合我上面说的"做好当下的任务";我在我这一层函数中我肯定要调用后面的一层函数呗,他怎么做我不管,我只要干好我现在的活就行了;那么在这个函数中,我现在的活是什么?是打印我这一层的cur_num,对吧;那么我只需要打印好我这一层的cur_num,就算我的任务完成了,之后的任务我就交给下一层的"工人";因此打印完之后就调用dfs(cur_num+0,n);对下一个"工人"下达指令,你去打印cur_num+1到n的数,你一定可以完成任务;
我们不要太过细致的在意每一个过程的种种细节,像中间会不会有哪一步出错呢?不会,无论在那一层我只要做好我的本职工作,然后剩下的交给后面的人,后面的人也是这样想的,那整个工程就不会出差错;这样看来是不是这个整个流程清晰多了;
别急,还有最后一个关键点,那就是出口;没有出口的函数就会无限调用,发生死循环;出口我们只需要考虑最后的一层情况,在这个题中最后的情况就是如果cur_num等于n的时候就是打印最后的n了,之后就不需要再调用函数打印了,这个时候就需要返回了;

综上所述:我们要清晰的完成一个DFS递归函数只需要考虑以下几点:
1.根据题目考虑出口的条件;
2.根据参数和题目,做好当前这一层的工作,然后调用下一层的DFS;
3.把DFS语句在脑海中想象成一句"你给我怎么怎么样,你一定能完成",然后坚定的调用它;
4.不要担心中间会出错,不要总想着函数调用的堆栈图,太抽象,很容易把自己绕蒙的;

下面就是题目练习环节,加深对DFS的理解;

汉诺塔问题

题目地址:. - 力扣（LeetCode）

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例1:

 输入：A = [2, 1, 0], B = [], C = []
 输出：C = [2, 1, 0]

示例2:

 输入：A = [1, 0], B = [], C = []
 输出：C = [1, 0]

提示:

1. A中盘子的数目不大于14个。

题目解析

题目的意思是要将盘子从A柱全部转移到C柱上,在转移的过程中我们可以借助另外的一个柱子辅助完成操作;

思路

假如现在A柱有n个盘子,那我们只需要将上面的n-1个盘子转移到B柱就可以了,这时候需要借助C柱辅助,然后再将A柱子上的一个盘子转移到C柱上即可;这就是我们这一层函数需要做的事情,然后就是确定出口条件,如果最后剩下一个盘子的时候,就不需要将0个盘子转移了,直接放在C盘上就可以了,然后return;

代码实现:

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}void dfs(vector<int>&a,vector<int>&b,vector<int>&c,int n){if(n==1){c.push_back(a.back());a.pop_back();return ;}//将a柱上的n-1个盘子,借助c柱子移动到b柱子上dfs(a,c,b,n-1);c.push_back(a.back());a.pop_back();dfs(b,a,c,n-1);}
};

合并两个有序的链表

题目地址:. - 力扣（LeetCode）

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

思路

这个题目中给的函数头其实就可以作为dfs的函数头使用;只需要给两个链表参数,然后dfs返回合并后的链表头指针;
好了,现在我们dfs函数的指令就是"你给我返回两个参数链表的合并后的头节点指针",那我们在自己这一层函数要做的就是确定返回谁和谁合并的问题;我们需要比较下两个形参的val值大小,然后返回小的节点的next和另一个链表的合并后的头结点指针(将绿框框里的两条链表合并后返回给我一个头结点指针);

最后确定出口,如果一条链表空了,那就返回另一条链表;

代码实现

class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(list1==nullptr)return list2;if(list2==nullptr)return list1;if(list1->val<=list2->val){list1->next=mergeTwoLists(list1->next,list2);return list1;}else{list2->next=mergeTwoLists(list1,list2->next);return list2;}}};

翻转链表

题目地址:. - 力扣（LeetCode）

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

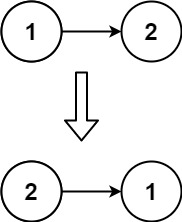
输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000

 思路

同样的,我们需要抽出一个节点ret,然后调用函数将ret->next为头节点的链表全部反转,并且返回反转后的头结点,其实就是最后一个节点,然后我们需要把head的节点和head->next节点的调整一下;

 最后的出口就是只剩下一个节点,或者如果链表本身就是空的,直接返回head即可;

代码实现

class Solution {
public:ListNode* reverseList(ListNode* head) {if(head==nullptr||head->next==nullptr)return head;ListNode* ret=reverseList(head->next);head->next->next=head;head->next=nullptr;return ret; }
};

两两交换链表中的节点

题目地址:. - 力扣（LeetCode）

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

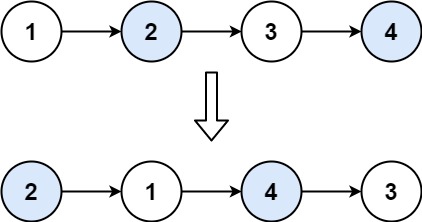
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

思路 

从前往后,两个两个的交换,不能改变节点的值,这道题与上道题没有什么差别,dfs可以认为是"返回链表交换后的头节点指针",然后对当前两个节点的操作;出口是剩下一个节点或者是没有节点;

代码实现 

class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head==nullptr||head->next==nullptr)return head;auto tmp=swapPairs(head->next->next);auto net=head->next;net->next=head;head->next=tmp;return net;}
};

快速幂

题目地址:. - 力扣（LeetCode）

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

思路

将一个幂分为两个幂;比如:3^7分成3^4*3^3,3^8分为两个3^4相乘;

除此之外还需要考虑n是负数的情况,如果n是负数,那么就应该调用函数1.0/dfs(x,-n);这里有个小细节,int的最大值是2^31-1如果是负数,那有可能传的是2^31,所以这种情况需要单独处理,或者使用long long解决; 

代码实现

class Solution {
public:double myPow(double x, int n) {return n>=0?dfs(x,n):1.0/dfs(x,-(long long)n);}double dfs(double x,int n){if(n==0)return 1.0;double  tmp=dfs(x,n/2);return (n%2==0)?1.0*tmp*tmp:tmp*tmp*x;}
};