动态规划算法——三步问题
1.题目解析
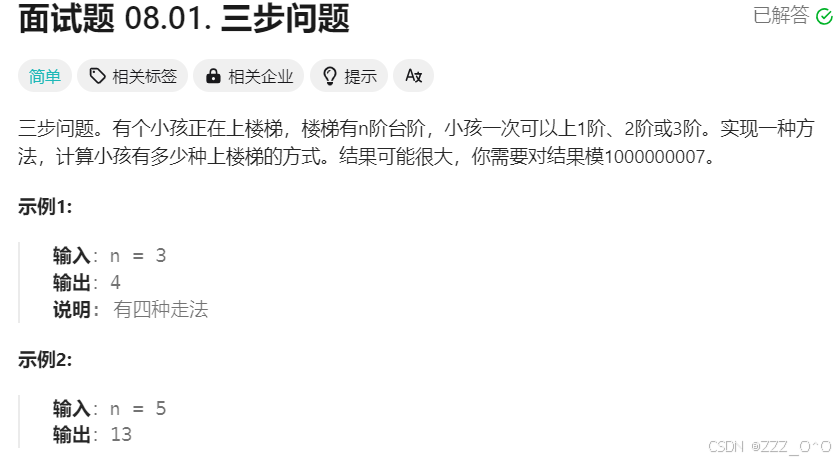
2.算法原理
本题可以近似看做泰波那契数列,即小孩到第一个台阶需要一步,到第二个台阶则是到第一个台阶的步数加上第一阶到第二阶的步数,同理第三阶就是第二阶的步数加上第二阶到第三阶的步数,由于小孩只能走三步,所以之后的位置就是该位置前三个位置的步数相加
3.实战代码
class Solution {
public:int waysToStep(int n) {const int MOD = 1e9 + 7;//处理边界if(n <= 2){return n;}else if(n == 3){return 4;}vector<int> dp(n + 1);//初始化dp[1] = 1;dp[2] = 2;dp[3] = 4;for(int i = 4;i <= n;i++){//状态转移方程dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;}return dp[n];}
};
