当前位置：首页 > news >正文

数据结构强化篇

news 2025/4/28 12:51:49

应用题

排序

在这里插入图片描述

插入排序

在这里插入图片描述

void InsertSort (ElemType A[], n int) {int i, j;for (i=2; i<=n; i++) //依次将 A[2]～A[n]插入前面已排序序列if (A[i]<A[i-1]) { //若 A[i]关键码小于其前驱，将 A[i]插入有序表A[0]=A[i]; //复制为哨兵，A[0]不存放元素for (j=i-1; A[0]<A[j]; --j) //从后往前查找待插入位置A[j+1]=A[j]; //向后挪位A[j+1]=A[0]; //复制到插入位置}
}

简单选择排序

思想：

每次从未排序的记录中选取最小关键字的记录，通过交换位置，加入已排序记录的末尾。

void SelectSort (ElemType A[], int n) {for (int i=0; i<n-1; i++) { //一共进行 n-1 趟int min=i;for (int j=i+1; j<n; j++) //在 A[i...n-1]中选择最小的元素if (A[j]<A[min]) min=j; //更新最小元素位置if (min!=i) swap (A[i],A[min]); //封装的 swap()函数共移动元素 3 次}
}

在这里插入图片描述

冒泡排序

从最后（最前）两个开始，两两比较，每次把最小的交换到前面。
每一趟都会确定一个元素的最终位置。
如果本趟和上一趟相同，就结束排序
是稳定的排序算法（两个元素大小相等不会交换）。

void BubbleSort (ElemType A[], int n) {for (int i=0; i<n-1; i++) {bool flag=false; //表示本趟冒泡是否发生交换的标志for (int j=n-1; j>i; j--) //一趟冒泡过程if (A[j-1]>A[j]) {swap(A[j-1],A[j]); //使用封装的 swap 函数交换flag=true;}if (flag==false) return; //本趟遍历后没有发生交换，说明表已经有序}
}

快速排序

思想：

从待排序的元素中选取一个基准元素，将所有比基准元素大的，放在右边，小的，放在左边。
先移动hight, 当找到小于基准元素的元素时，就将其放到low位置，然后再移动low，直到low==hight。
然后对左右两个子表进行递归。

效率分析：
快排的时间复杂度为：n*递归深度
因此，快排的速度与递归搜索树的高度息息相关。


// 用第一个元素将待排序序列划分成左右两个部分
int Partition(int A[], int low, int high) {int pivot = A[low]; // 第一个元素作为枢轴while (low < high) { // 用 low、high 搜索枢轴的最终位置while (low < high && A[high] >= pivot) --high;A[low] = A[high]; // 比枢轴小的元素移动到左端while (low < high && A[low] <= pivot) ++low;A[high] = A[low]; // 比枢轴大的元素移动到右端}A[low] = pivot; // 枢轴元素存放到最终位置return low; // 返回存放枢轴的最终位置
}// 快速排序
void QuickSort(int A[], int low, int high) {if (low < high) { // 递归跳出的条件int pivotpos = Partition(A, low, high); // 划分QuickSort(A, low, pivotpos - 1); // 划分左子表QuickSort(A, pivotpos + 1, high); // 划分右子表}
}

归并排序

思想
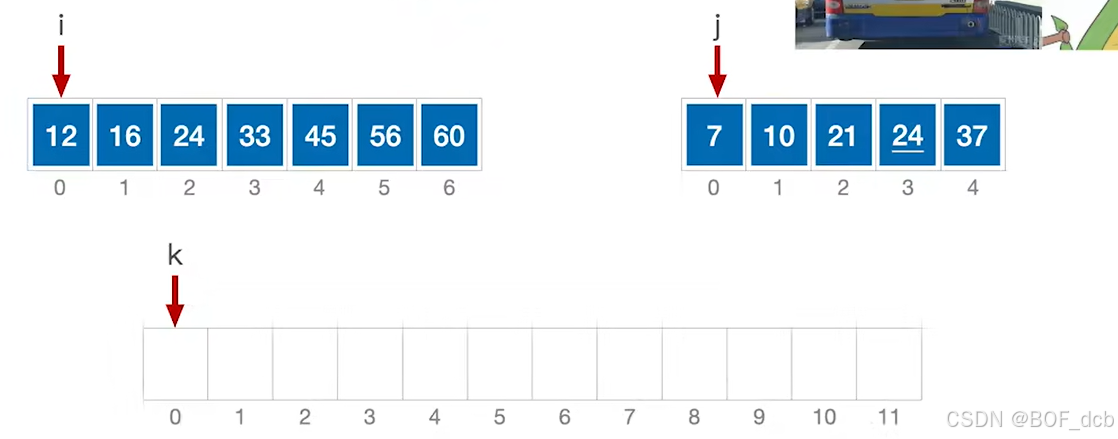
在这里插入图片描述

假设两个有序序列，每次将i和j所指向元素中的最小元素插入k所指位置，k后移。
当一个序列所有元素插完后，就将另一个序列所有剩余元素插入到我们生成的有序序列末尾。
因此，当给我们一个无序序列时，我们可以先将所有元素两两一组，进行排序，然后递归合并。

代码实现

int *B = (int *)malloc(n * sizeof(int)); // 辅助数组B// A[low...mid]和A[mid+1...high]各自有序，将两个部分归并
void Merge(int A[], int low, int mid, int high) {int i, j, k;for (k = low; k <= high; k++) // 将A中所有元素复制到B中B[k] = A[k];for (i = low, j = mid + 1, k = i; i <= mid && j <= high; k++) {if (B[i] <= B[j])A[k] = B[i++]; // 将较小值复制到A中elseA[k] = B[j++];}// forwhile (i <= mid) A[k++] = B[i++];while (j <= high) A[k++] = B[j++];
}void MergeSort(int A[], int low, int high) {if (low < high) {int mid = (low + high) / 2; // 从中间划分MergeSort(A, low, mid); // 对左半部分归并排序MergeSort(A, mid + 1, high); // 对右半部分归并排序Merge(A, low, mid, high); // 归并}
}