1.凸包、极点、极边基础概念
目录
1.凸包
2.调色问题
3.极性(Extrem)
4.凸组合(Convex Combination)
5.问题转化(Strategy)编辑
6.In-Triangle test
7.To-Left-test
8.极边(Extream Edges)
1.凸包

凸包就是上面蓝色皮筋围出来的范围
这些钉子可以转换到坐标轴中,横纵坐标表示颜色的比例
2.调色问题

上述问题可以进行一个抽象,抽象为一个color space

结论
- 如果有1种颜料可以被2种颜料勾兑出来,它必然位于二者之间的那条连线上
- 如果有1种颜料可以被3种颜料勾兑出来,它必然位于三角形内
- 勾兑比例与距离成反比
3.极性(Extrem)

蓝色的为极点
极点上存在一条直线,使得所有的点落在它的一侧
4.凸组合(Convex Combination)

为什么最小值必须>=0 ?
因为这种颜色大不了不用,但也不可能是负的
5.问题转化(Strategy)

如果是极点那么久不可能在一个三角形的内部,所以采用排除法,剩下的就是极点
6.In-Triangle test

遍历所有可能的三角线组合,排除非极点
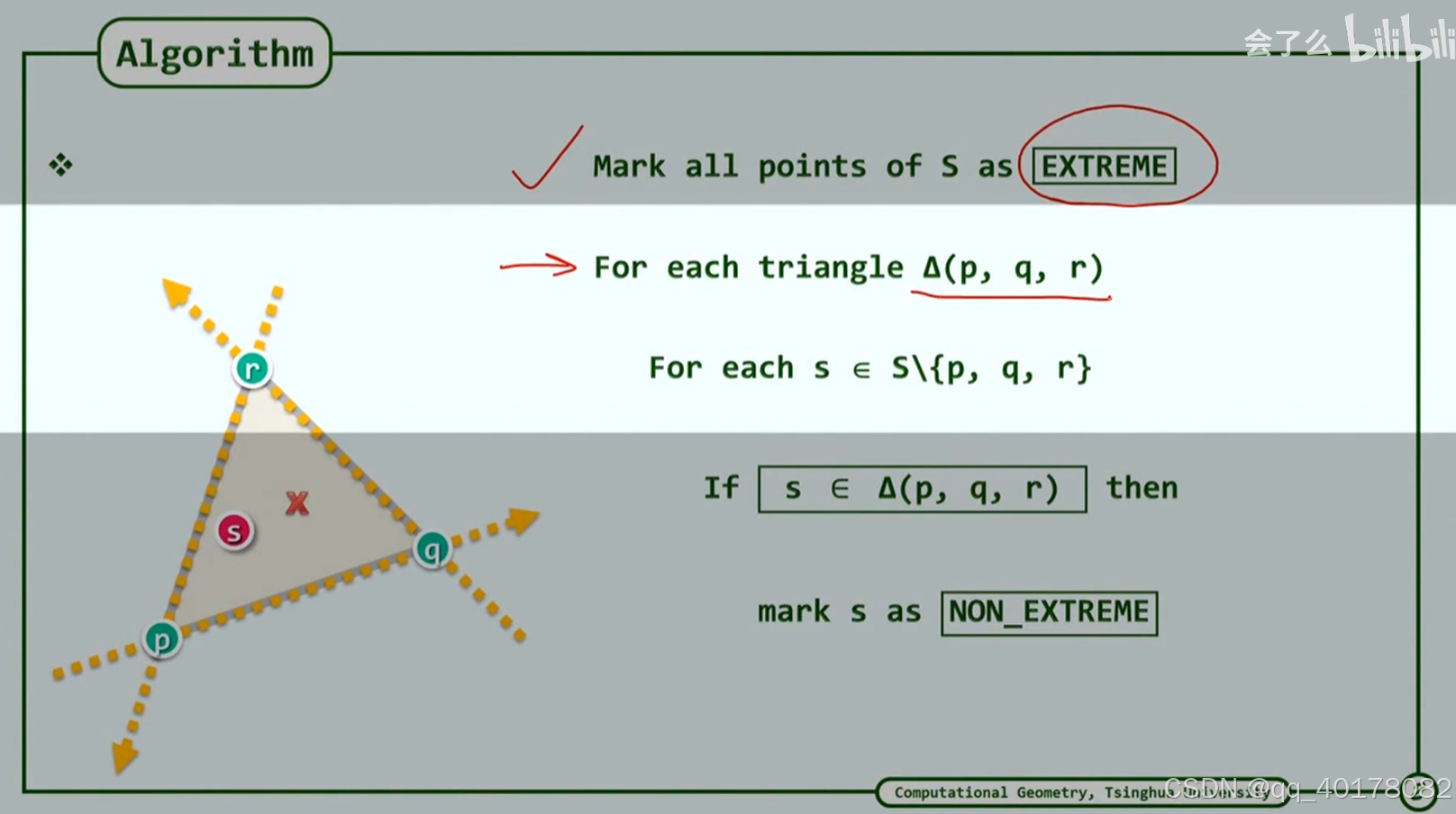
低效做法

更加聪明的做法,如果一个点位于三条直线的left,那么它一定位于三角形内
7.To-Left-test
如何高效的判断一个点是否是包含在一个三角形的内部是计算几何里的一个基础问题。
In Triangle Test问题也可以用来解决计算几何里的一个基础问题就是 凸包问题 。
问题描述:
给出一个点s,判断其是否在一个三角形(p, q, r)内部。
问题求解:
 判断一个点是否在三角形内部等价于对于三条边分别做To left test的结果一致。
判断一个点是否在三角形内部等价于对于三条边分别做To left test的结果一致。
那么现在的问题就是如何高效和精确的实现To left test。
只有s位于pq这条线段左侧才会取正。
关于这个可以使用空间坐标系的海伦公式来求解。
| p.x p.y 1 |
2 * S = | q.x q.y 1 |
| s.x s.y 1 |
并且这个公式是有向的,当三个点是逆时针排列的时候该行列式的返回结果是正数,当三个点是顺时针排列的时候行列式的返回结果是负数。
| 1 2 3 4 5 6 7 8 |
|
To left test 几乎贯穿了整个计算几何,不仅是计算凸包的核心,也是很多其他计算几何问题的关键算法。
例如:判断两条线段是否相交,只需要做4次to left test即可。
8.极边(Extream Edges)
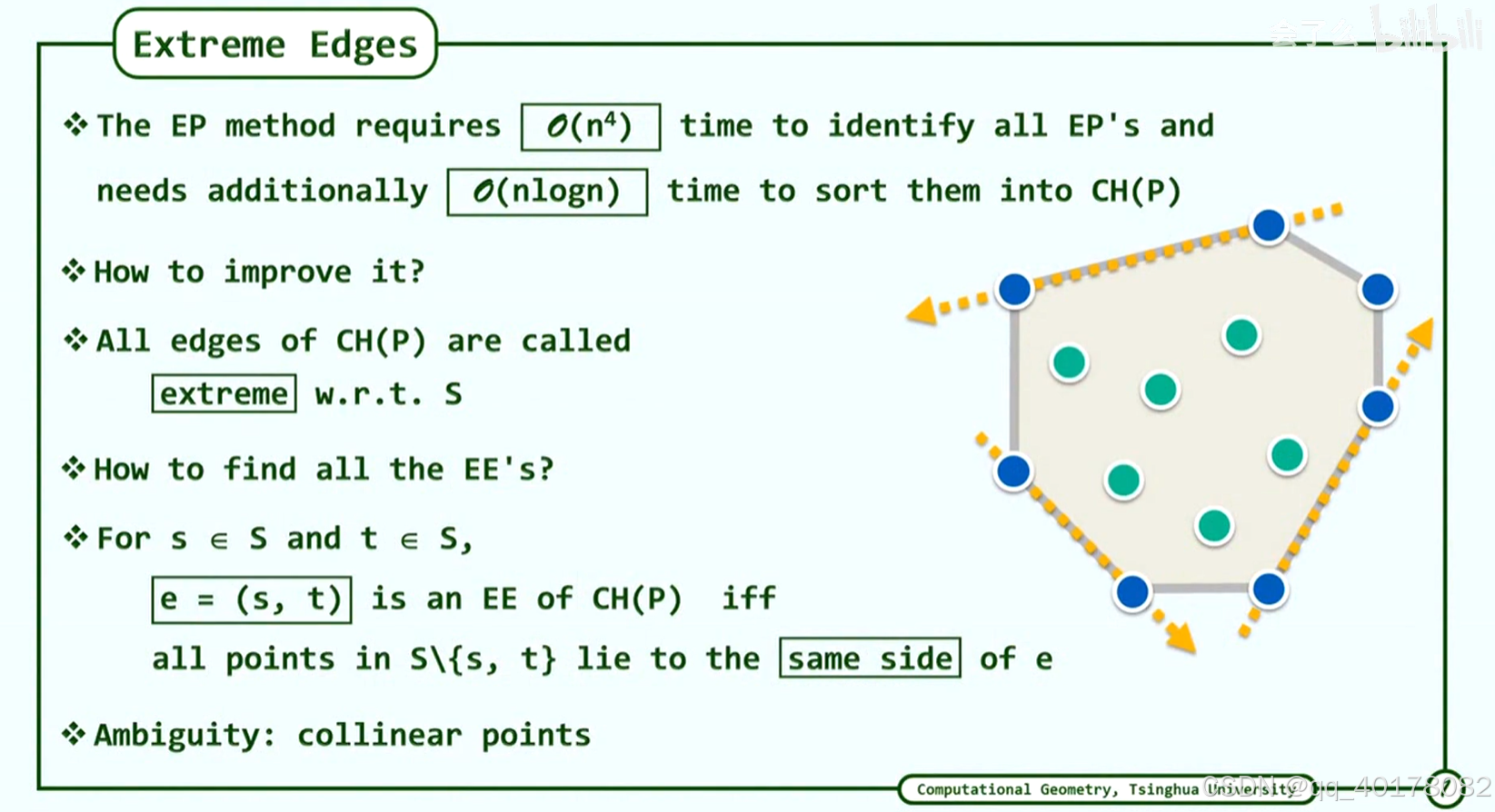
极边:所有的点落在同一侧,就是极边
算法实现



极边的算法效率高于极点的算法效率
参考
In Triangle Test / To Left Test - hyserendipity - 博客园
