论文学习—VAE
VAE----Auto-Encoding Variational Bayes
- 2024年12月17日-2024年12月18日
- 摘要
- 引言
- 方法
- 例子:变分自动编码器
2024年12月17日-2024年12月18日
从今天开始,我准备记录自己学习的内容以此来检验我每天的学习量,菜鸡一枚,希望能够与大家进行沟通交流。我的第一篇论文学习选择的是VAE,因为我对于这种生成模型比较感兴趣。
论文链接: Auto-Encoding Variational Bayes
https://blog.csdn.net/a312863063/article/details/87953517
摘要
摘要告诉我们,作者引入了一种随机变分推理和学习的算法用于解决难以拟合后验分布的问题,即作者通过利用概率表述潜在空间进而拟合后验模型。
贡献: Our contributions are two-fold. First, we show that a reparameterization of the variational lower bound
yields a lower bound estimator that can be straightforwardly optimized using standard stochastic gradient methods. Second, we show that for i.i.d. datasets with continuous latent variables per datapoint, posterior inference can be made especially efficient by fitting an approximate inference model (also called a recognition model) to the intractable posterior using the proposed lower bound estimator. Theoretical advantages are reflected in experimental results.
摘自原文,一般来说论文会在两个地方写自己的贡献:摘要和引言,但是这篇论文只在摘要提到了自己的贡献,可能是因为觉得必要写吧。 (不愧是大神 )
作者的贡献表明,他们从理论上证明了变分下界的重新参数化会产生了一个下界估计量,它可以直接使用标准的随机梯度方法进行优化。而且对于对于每个数据点具有连续潜变量的数据集来说,他们通过使用所提出的下界估计量将近似推理模型可以拟合到难以处理的后验模型。
引言
这篇论文引言很短,只有两段话,第一段介绍了目前的研究希望可以拟合棘手的后验分布,但是目前的工作却难以解决,所以作者发现变分下界的重新参数化会产生下界的一个简单的可微无偏估计量,利用这个估计量可以拟合后验分布并且很容易进行优化。第二段则是简单介绍了他们提出的算法(AEVB)。(我觉得没什么东西,只是说了一下他们的方法可以只对少量数据抽样就可以进行学习然后拟合后验模型从而完成各种任务。)
方法
这部分涉及到了证明,如果感兴趣的同学可以仔细研究一下论文内容,我只做简单介绍,我这里就不再赘述了。(主要是我懒而且菜鸡不喜欢也学不会这种数学证明)
这篇论文确实挺奇怪,一般引言后面介绍是相关工作,但是作者直接开始讲方法却把相关工作放在了第四部分。可能是想让大家直接知道他们是怎么做的。(我猜的,毕竟大神的想法我这个菜鸡怎么懂 )
方法部分主要是用于推导各种具有连续潜变量的有向图形模型的下界估计量,即证明部分也是作者提到自己的第一个贡献点,他们选择每个数据点具有潜在变量的数据集。

这个图介绍了基于潜在变量的生成模型的流程,正如作者所示实线表示生成模型,虚线表示难以处理的后验的变分近似。
2.1介绍了问题定义,没什么东西,就是介绍采用什么变量表示什么内容,目前遇到的一些问题以及如何进行一些简化。我觉得大家可以重点读一下最后一段了解一些编码器和解码器就行。
2.2变分边界 这个涉及了对于下界估计量的推导,文中是一个简单的版本只是告诉我们最终的推导结果。

2.3 SGVB估计器和AEVB算法 介绍了整个算法的推导流程以及数学证明,作者通过推导告诉我们如何对这些参数进行优化,也介绍了如何进行这样的优化。
如果大家想进一步了解可以参考这篇博客,博客的这个图也很形象告诉我们为什么作者要这么做。(作者不愧为天才这都能想出来,膜拜膜拜)

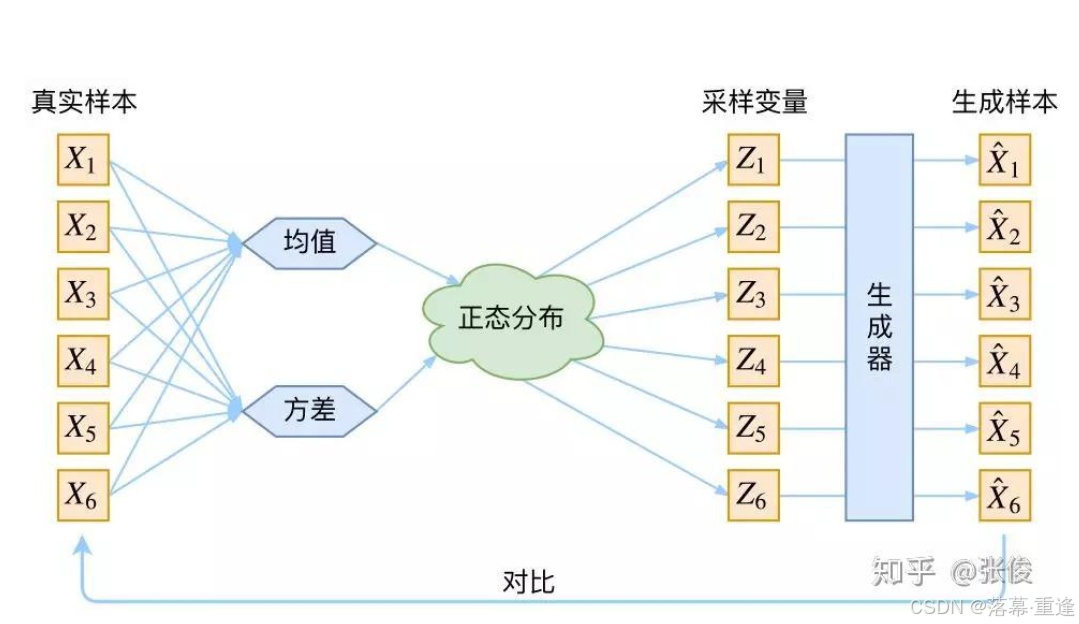
2.4重新参数化技巧这一部分介绍了他们的方法是如何起效果,通过这一部分我发现这篇论文主要是为了告诉我们给定一个真实样本 Xk,我们可以假设存在一个专属于 Xk 的分布 p(Z|Xk)(后验分布),并假设这个分布是(独立的、多元的)正态分布。,那么从 p(Z) 中采样一个 Z,那么我们就可以知道这个 Z 对应于哪个真实的 X 了, p(Z|Xk) 专属于 Xk,我们有理由说从这个分布采样出来的 Z 应该还原到Xk 中去。
例子:变分自动编码器
这一部分作者介绍了一个例子,通过这个例子我们对作者的方法可以有更深入的了解,而且如果大家跟我一样不像看前面的推导过程的话,大家可以好好研究一下这一部分,毕竟直观的例子更方便我们理解。公式(9)告诉我们后验概率的分布定义,公式(10)告诉我们我们针对于这个例子的目标函数。通过优化我们可以实现拟合后验模型,而根据后验模型我们就可以得到原始分布即达到生成数据的目的。

可能文字不太直观,大家可以参考这篇知乎和这篇博客的内容。

之后就是相关工作、实验、结论等内容,大家可以看原文,我就不给大家献丑了。
本人水平有限肯定存在很多不足之处,欢迎大家进行交流。若是大家觉得看不懂我写的,推荐大家可以参考一下内容:
博客(强烈推荐!!!)
知乎
CSDN
