模电期末笔记 (包过版)
文章目录
- 一、直流电路
- 公式
- 题型一:电压源与电流源求电压,电流,功率
- 题型二:基尔霍夫定律求电压,电流
- 题型三: 理想电源的等效变换
- 题型四:求复杂电路的电压,电流,电功率
- **题型五:分析受控源的电阻电路**
- 二、扩展知识
- 电容器
- 电感线圈(电感器)
- 三、正弦稳态电路分析
- 正弦交流电的基本概念:
- 正弦量的向量表示
- 基尔霍夫定律的向量表示
- 3种基本元件伏安关系的向量形式
- 电阻元件 R
- 电感元件 L
- 电容元件 C
- 简单正弦交流电路
- RLC 串联交流电路
- 阻抗的串并连
- 正弦稳态电路的分析(必考)
- 四、半导体二极管及直流稳压电源
- 知识总结
- 二极管的常见结构:
- 二极管的伏安特性
- 晶体二极管电路的分析方法
- 简化电路模型
- 晶体二级管电路的分析方法(重点)
- 实战演练
- 五、晶体三极管及其放大电路
- 晶体三级管的外部特性
- 晶体管的类型及符号
- 晶体管的电流分配与`放大作用`
- 晶体管的共射特性曲线
- 输入特性曲线:
- 输出特性曲线:
- 截止区
- 放大区
- 饱和区
- 放大电路的组成和工作原理(了解)
- 放大电路的分析(重点)
- 直流通路与交流通路
- 静态分析
- 放大电路的直流通路
- 图解法确定静态值
- 动态分析(放弃,建议彻底弄懂以上部分(肯定能过的))
- 微变等效电路法
- 图解法
- 图解法分析放大电路的非线性失真和动态范围
一、直流电路
公式
i ( t ) = d q d t i(t) = \frac {dq} {dt} i(t)=dtdq
u ( t ) = d w d q u(t) = \frac {dw} {dq} u(t)=dqdw
p ( t ) = d w d t p(t) = \frac {dw} {dt} p(t)=dtdw
P = U I P=UI P=UI
w ( t ) = ∫ − ∞ t P ( λ ) d λ w(t) = \int_{-\infty}^t P(\lambda) d\lambda w(t)=∫−∞tP(λ)dλ
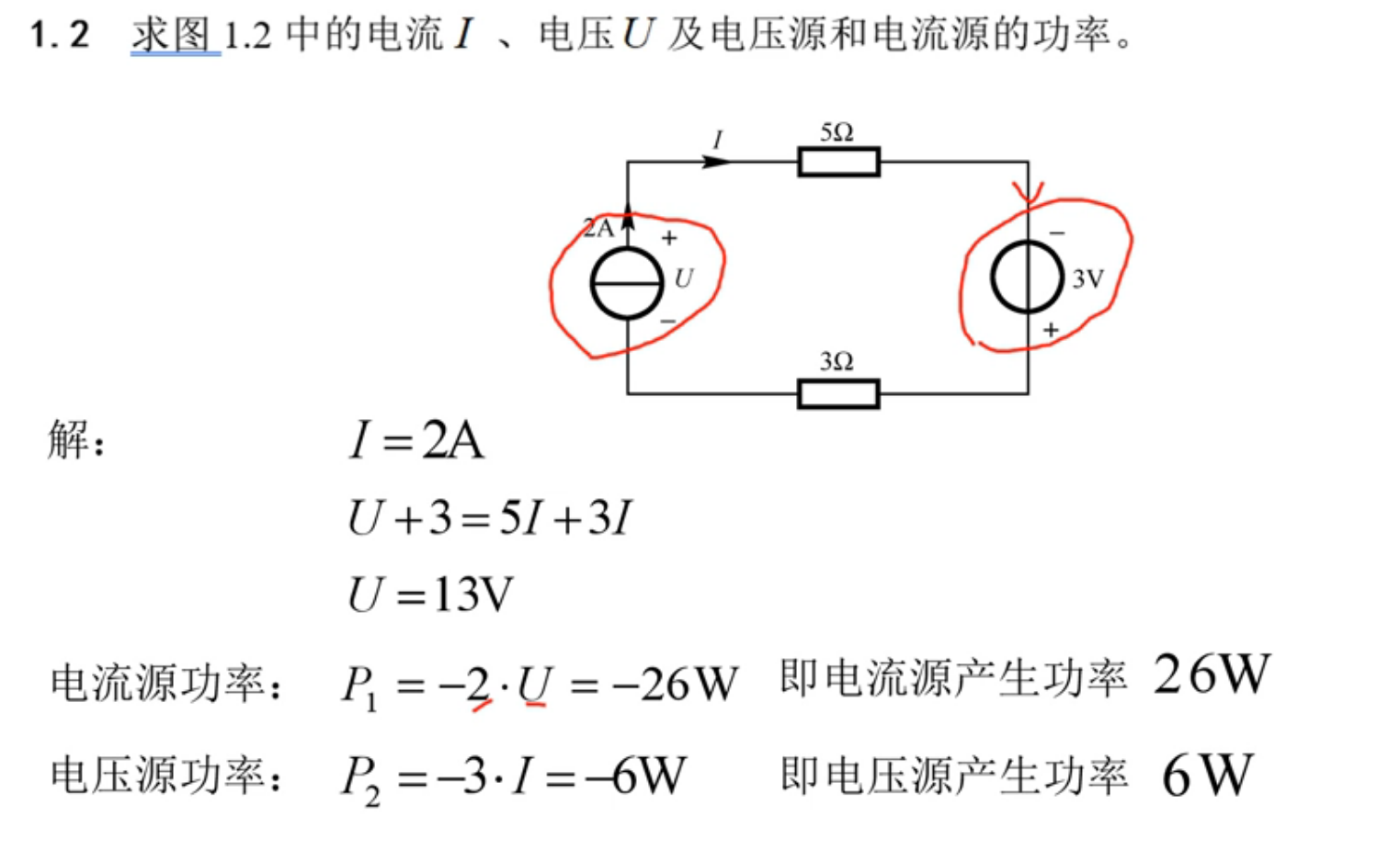
题型一:电压源与电流源求电压,电流,功率
- 电压与电流的参考方向
- 功率和能量
- 提供电功率的称为
电源,吸收电功率的称为负载
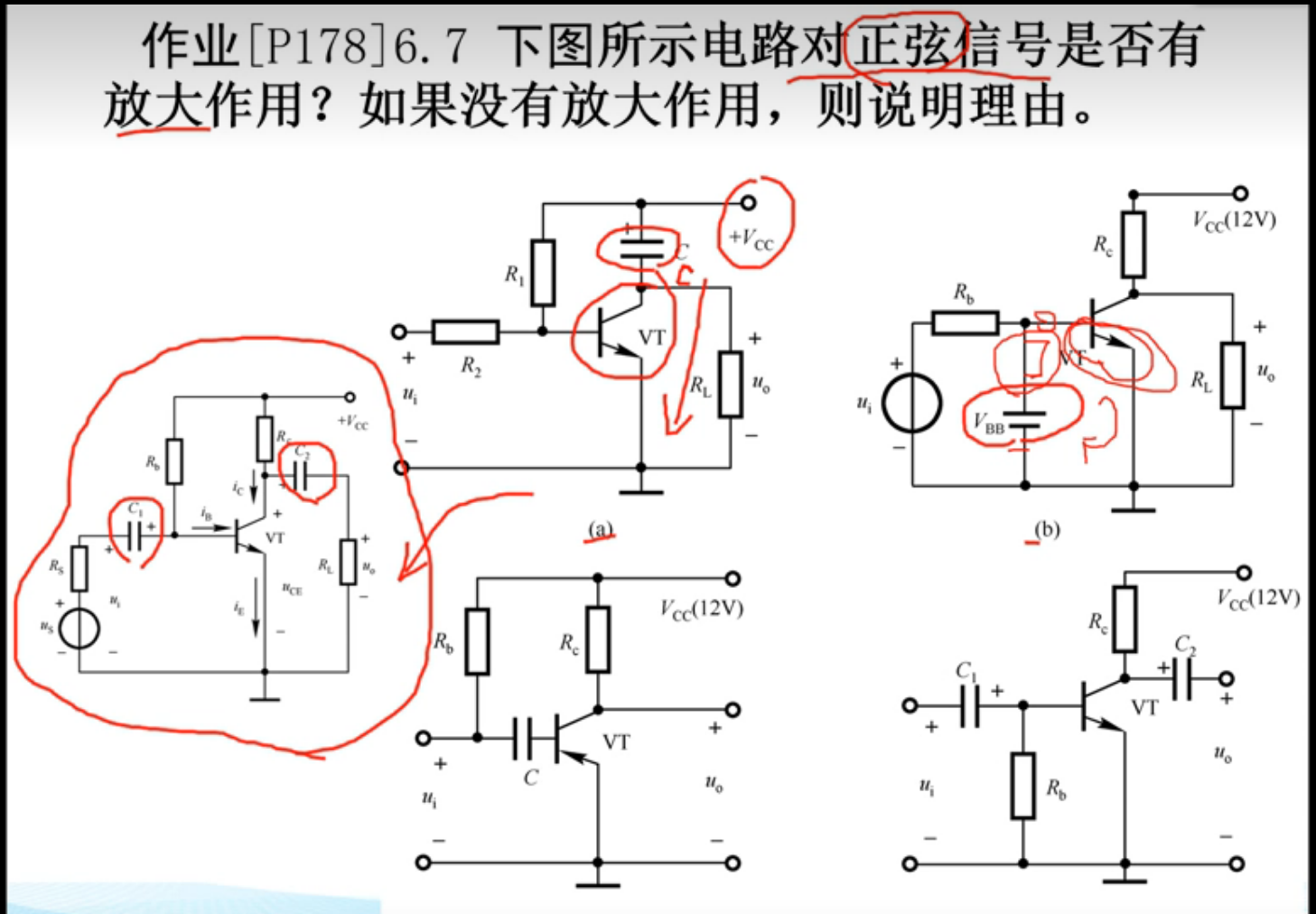
题型二:基尔霍夫定律求电压,电流
支路:一个两端元件视为支路
节点:两条或是两条以上支路
回路:电路中任一闭合路径称为回路
网孔: 在回路内部不另含支路的回路称为网孔
KCL: 在任一时刻,对任一节点,流出(或流入)该节点的所有电流的代数和等于零
KVL: 在任一时刻,对任一回路,沿着指定的回路绕行方向,各元件两端的电压的代数和为零
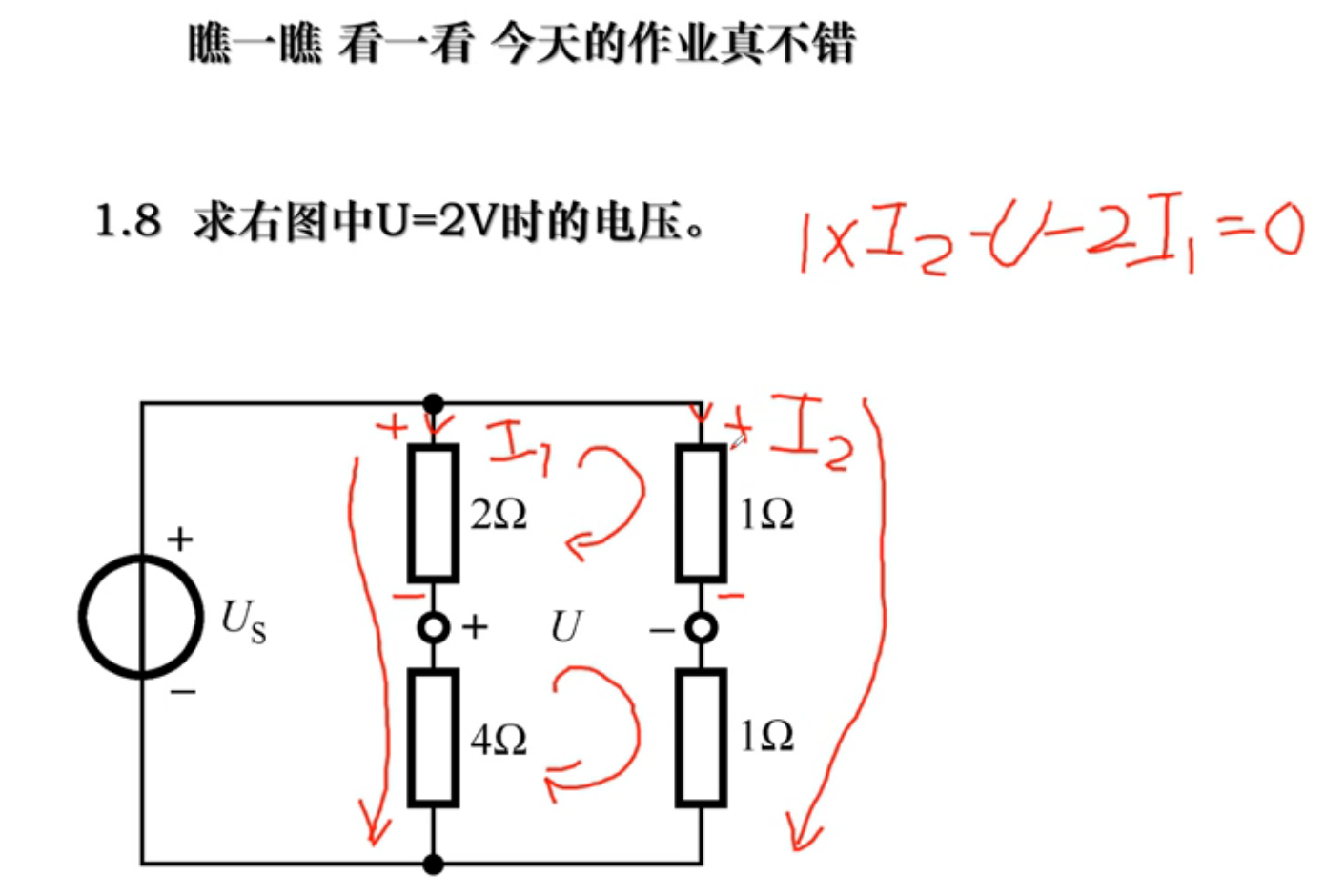
题型三: 理想电源的等效变换
电压源的串联及等效,电流源的并联及等效电压源与元件的并联,电流源与元件的串联(电压源的极性与大小必须相同,否则不允许串联。电流源的方向和大小必须完全相同,否则不允许串联)
实际
电压源和实际电流源的等效
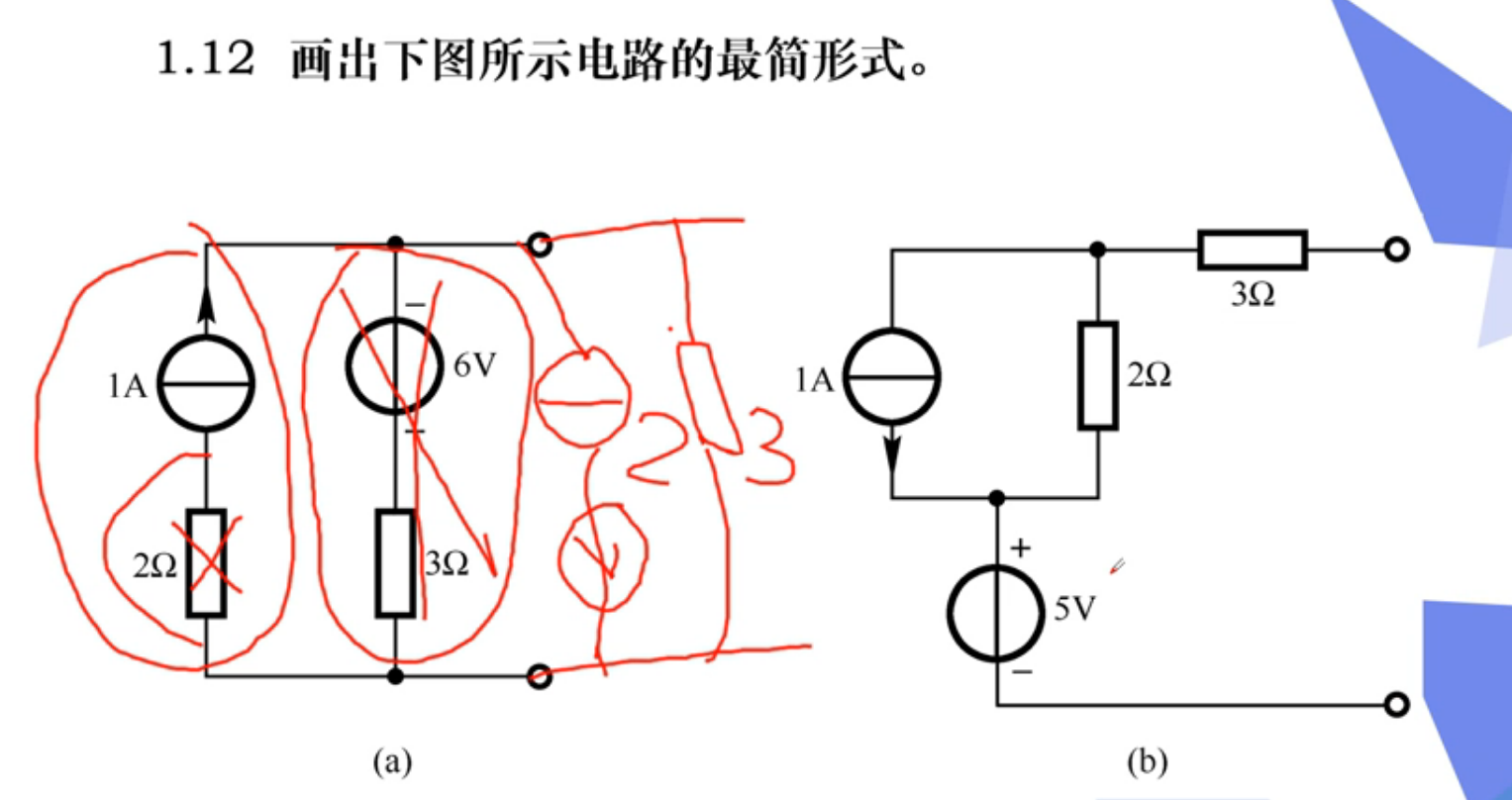
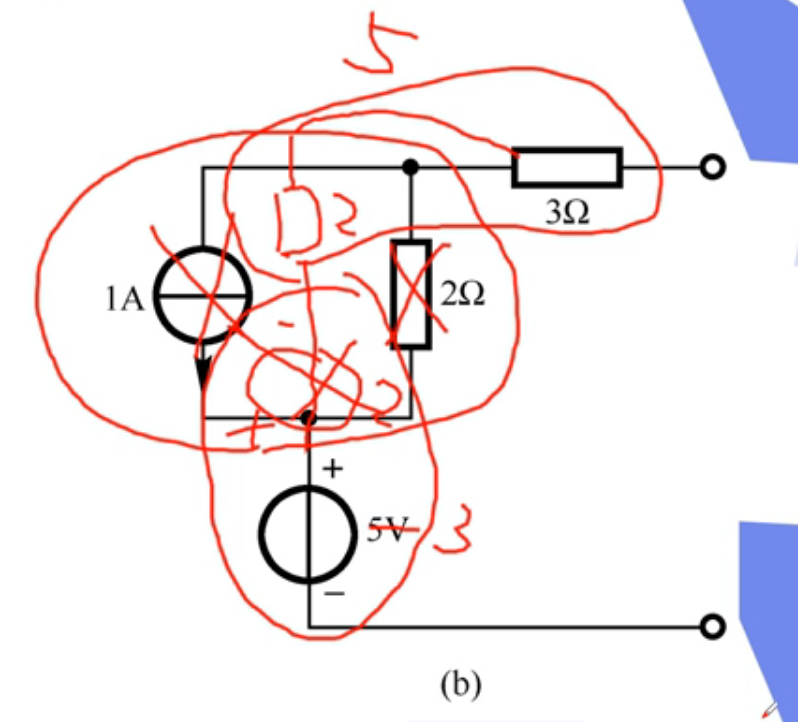
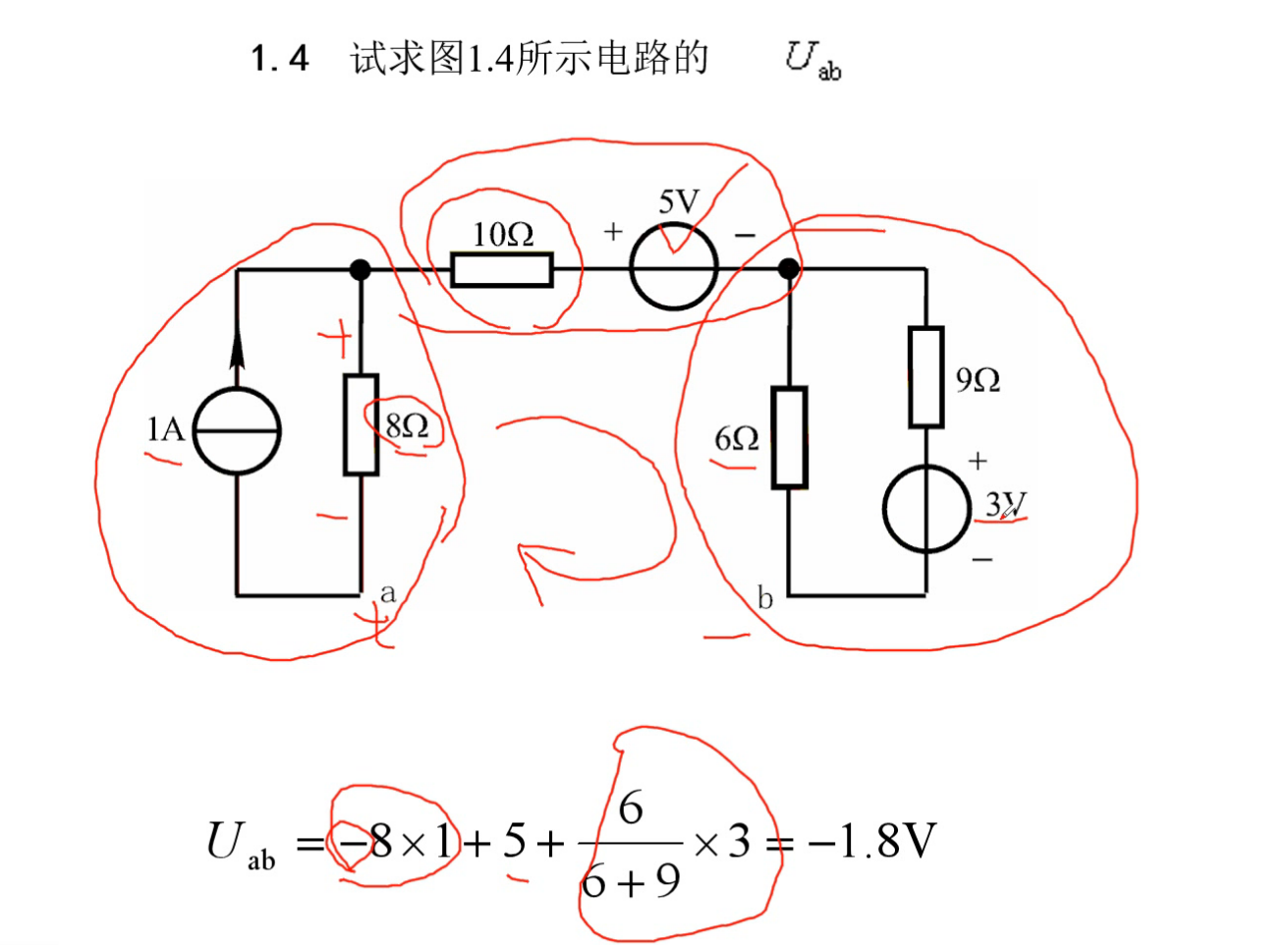
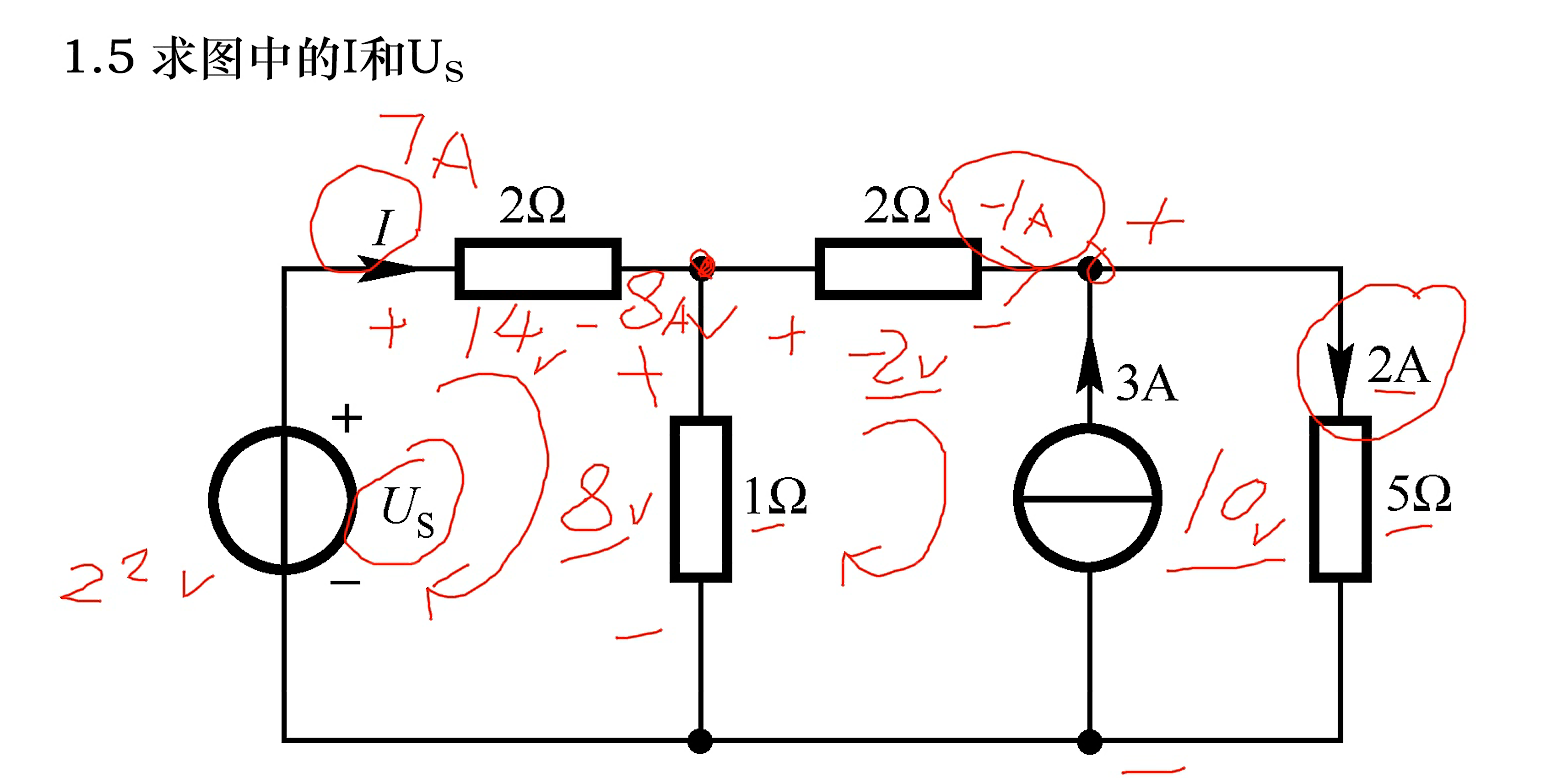
题型四:求复杂电路的电压,电流,电功率
电位必须要有一个参考点:通常选定与金属外壳相连的点作为
参考点点位为0
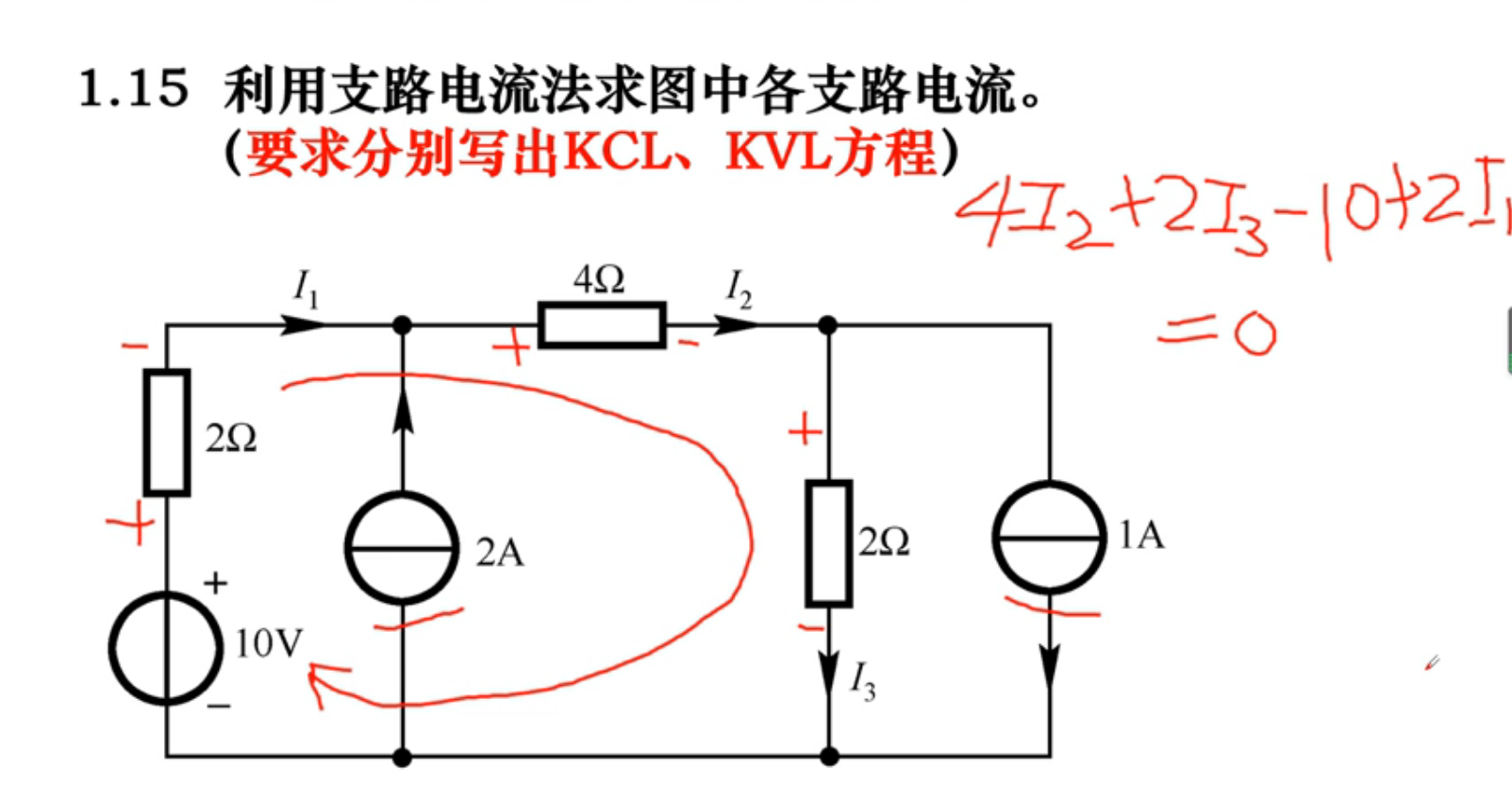
支路电流分析法:
- 标出每个支路电流以及参考方向
- 根据 KCL 列出 n - 1 个独立的节点电流方程
- 选定所有独立回路并指定每个回路的绕行方向,再根据 KVL 列出 b-(n-1) 个回路电压方程
- 求解 (2) (3) 所列的方程组,得各支路电流
- 根据需要,利用元件 VAR 可求得各元件电压及功率
节点分析法:在电路中任选一个节点作为参考节点,则其他节点到参考节点的电压降称为该节点的节点电压
叠加定理:当某一独立源单独作用时,其余的独立源置为零。叠加取正,相反时取负。🆘 只适用于电压与电流的计算
等效电源定理:只需求出复杂电路中某一特定支路的电流或电压时,把待求支路从网络中拉出来,吧它看做外电路,而把其余部分看做是线性有源单口网络
戴维南定理:当等效电源模型为实际电压源时
诺顿定理:当等效电源模型为实际电流源时
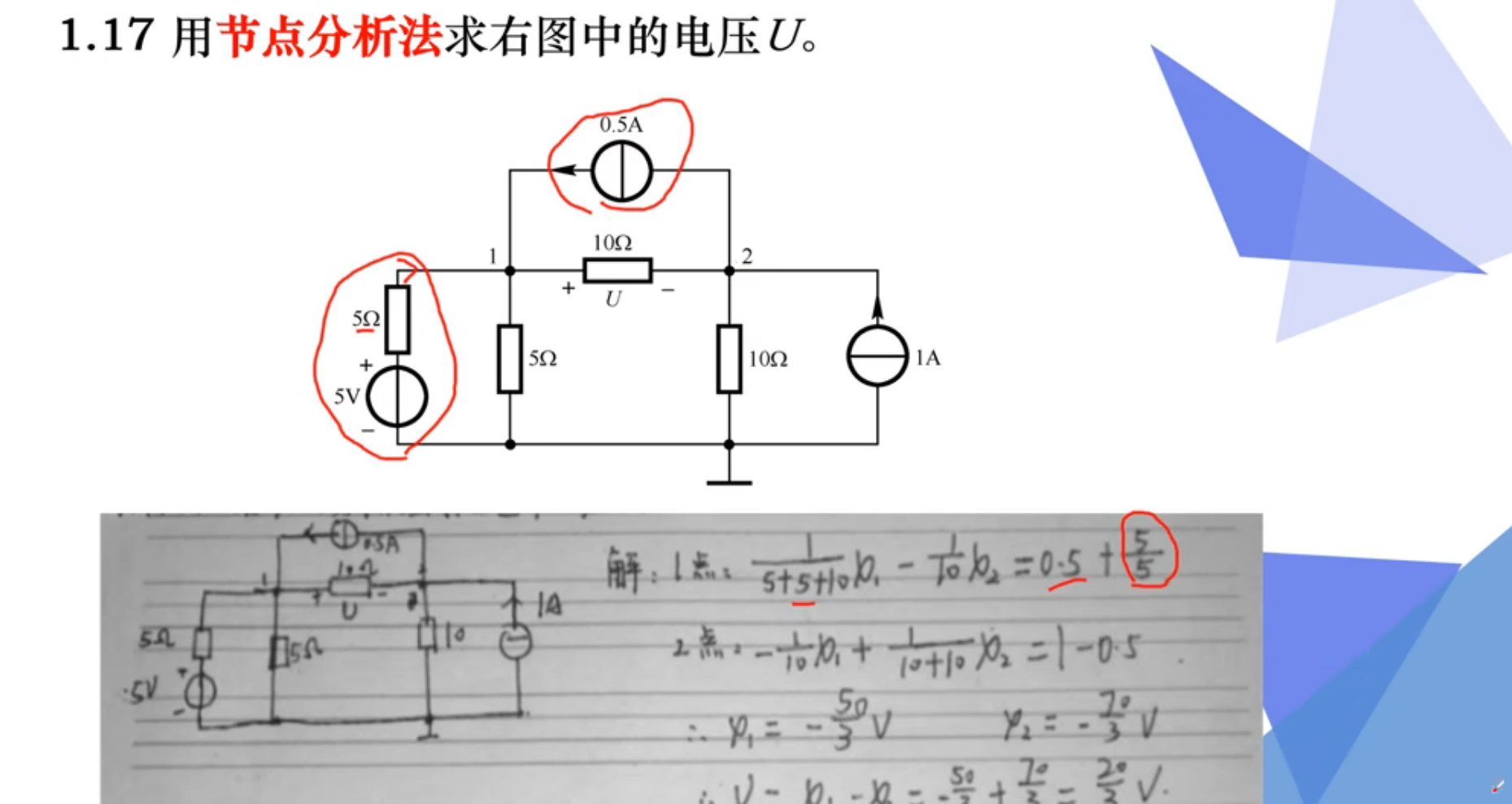
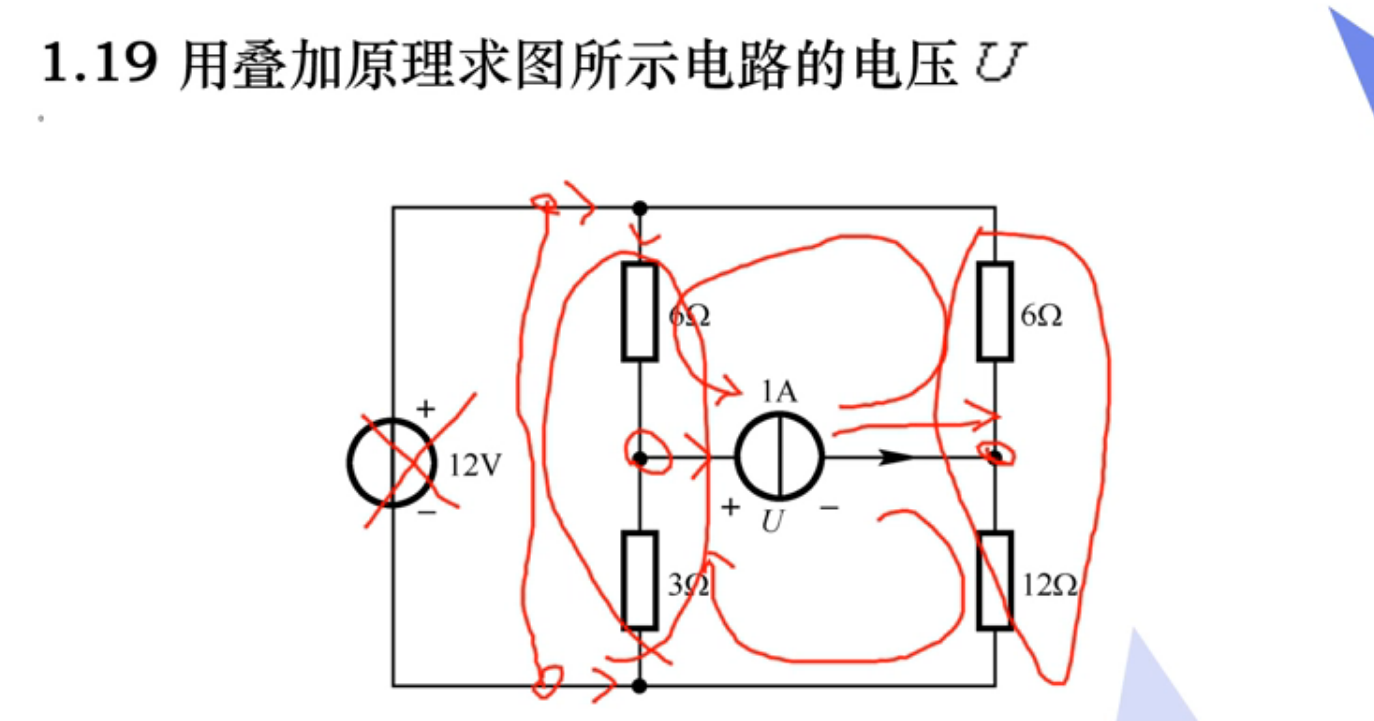
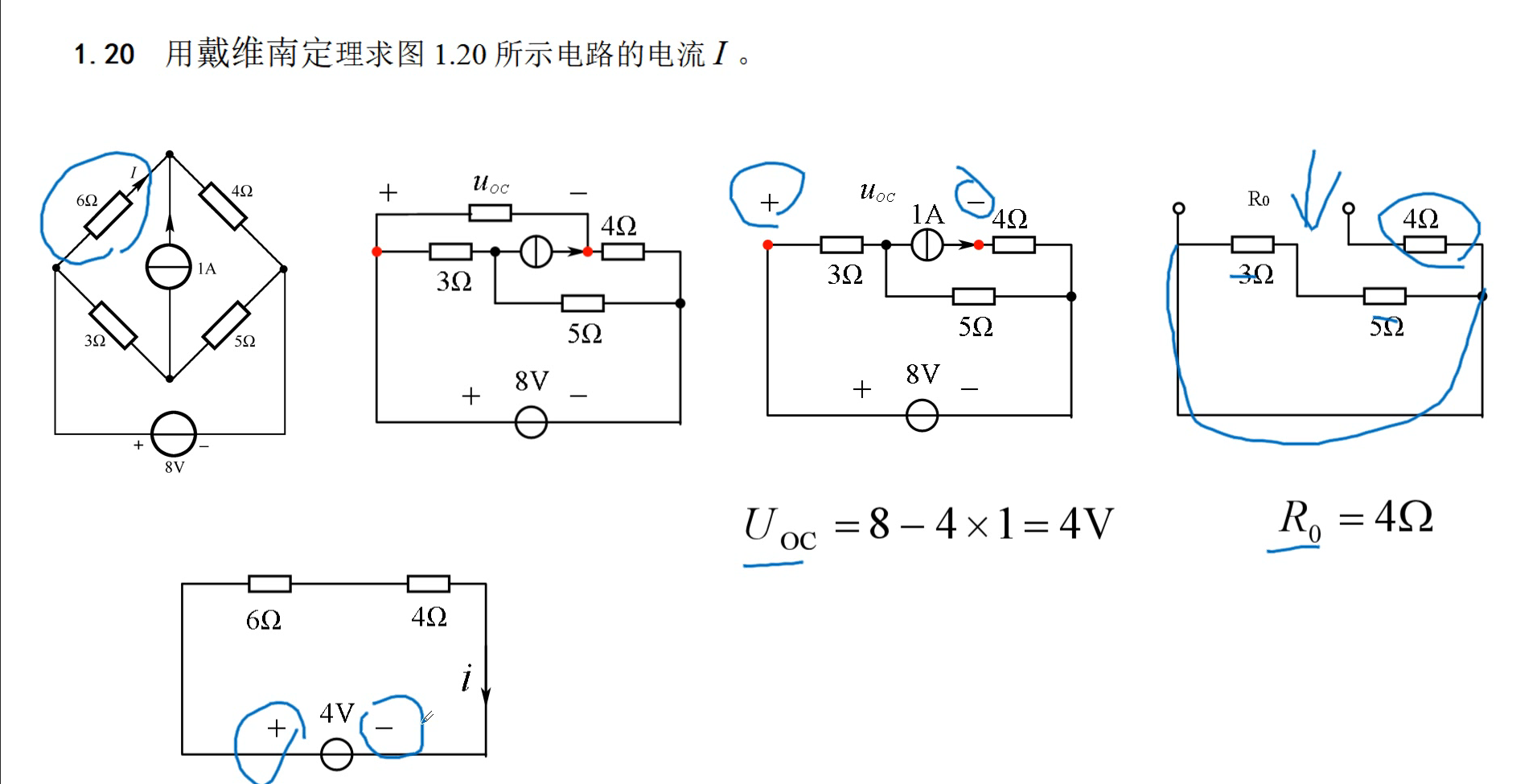
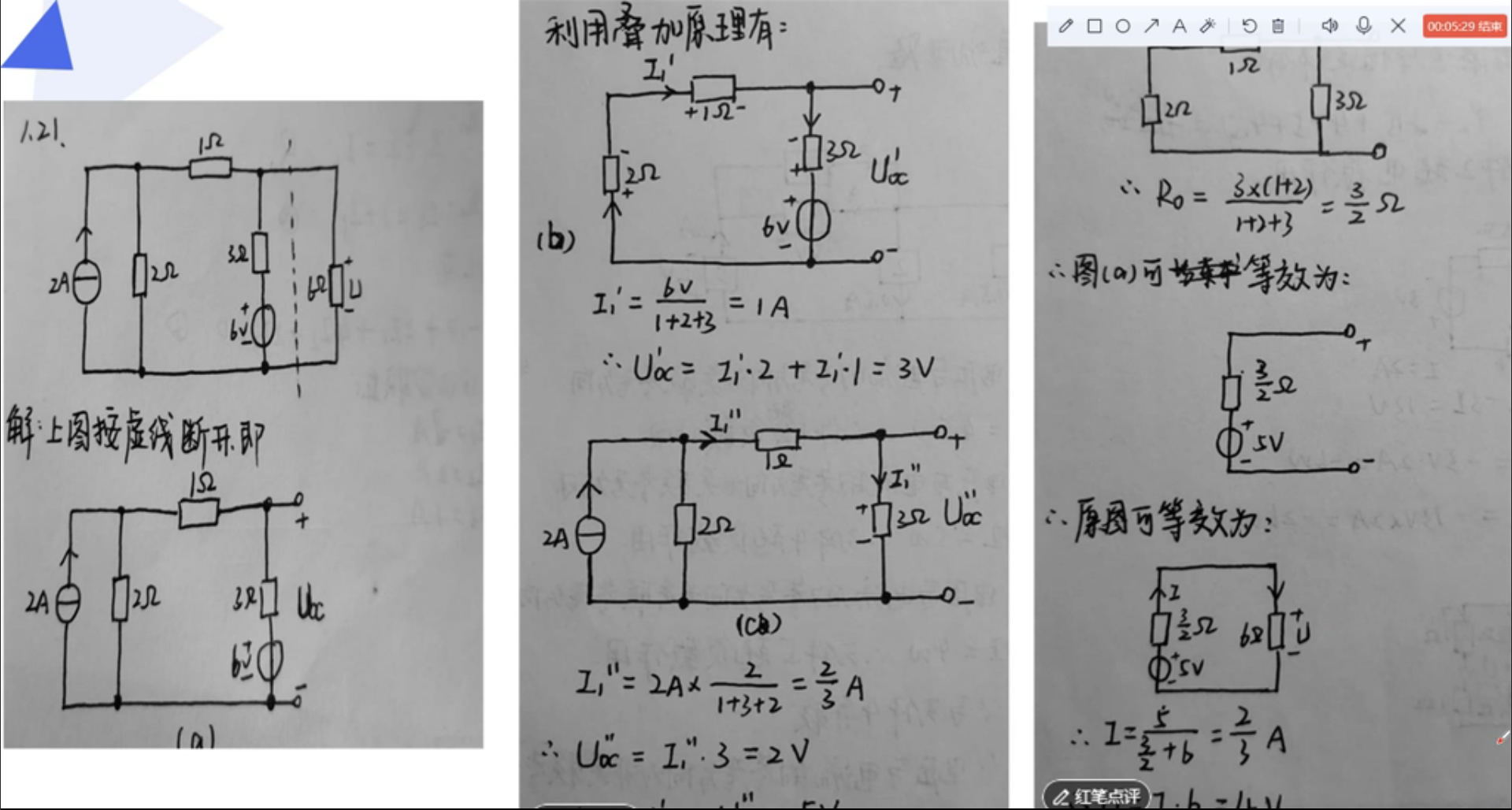
题型五:分析受控源的电阻电路
受控源:电压源的电压和电流源的电流受到同一电路中其他支路的电压或电流控制.用棱形符号表示
- 电压控制电压源 (Voltage-Controlled Voltage Source) VCVS
- 电压控制电流源 (Voltage-Controlled Current Source) VCCS
- 电流控制电流源 CCVS
- 电流控制电压源 CCCS
受控源等效: 对含受控源电路进行等效时,应在电路中保留控制量支路
支路法: 利用支路法计算含受控源的电路时,可将受控源视为独立源处理
叠加法: 受控源不是独立源,不可单独作用
等效电阻: 对含受控源的等效电阻计算不能直接用简单的串并联求解
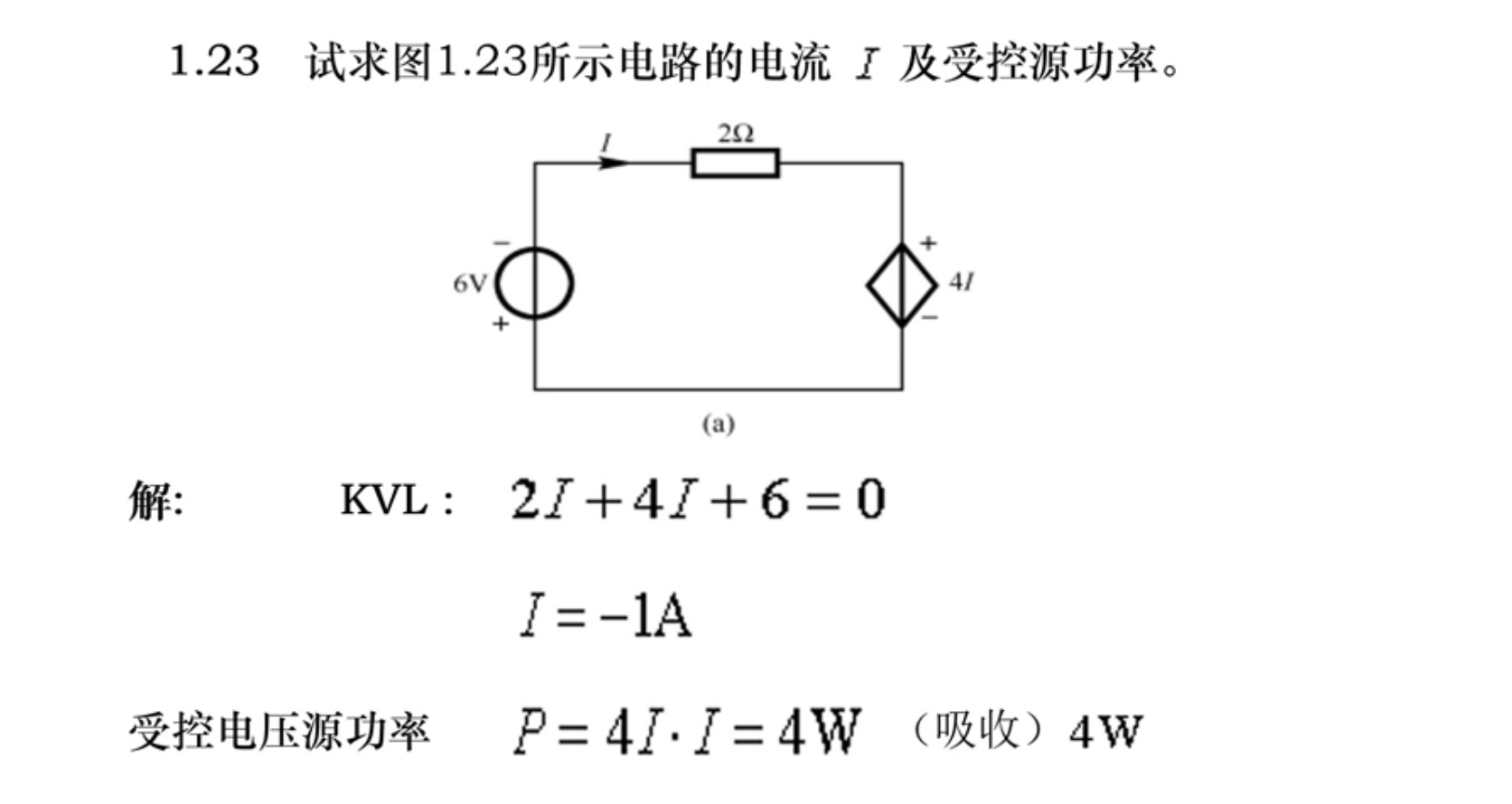
二、扩展知识
电容器
电容器是一个
存储电荷或者说存储电场能量的元件。通直阻交C = q u C = \frac {q} {u} C=uq
i = d q d t = d C u d t = C d u d t i = \frac {dq} {dt} = \frac {dCu} {dt} = C\frac {du} {dt} i=dtdq=dtdCu=Cdtdu
两边同时积分:
u ( t ) = 1 C ∫ ∞ t i ( λ ) d ( λ ) u(t) = \frac {1} {C} \int_{\infin}^t i(\lambda)d(\lambda) u(t)=C1∫∞ti(λ)d(λ)
p ( t ) = u ( t ) i ( t ) = C u d u d t p(t) = u(t)i(t) = Cu \frac {du} {dt} p(t)=u(t)i(t)=Cudtdu
W c ( t ) = ∫ − ∞ t p ( λ ) d ( λ ) = 1 2 C u 2 ( t ) − 1 2 C u 2 ( − ∞ ) = 1 2 C u 2 ( t ) W_c(t) = \int_{-\infin}^tp(\lambda)d(\lambda) = \frac {1} {2}Cu^2(t) - \frac {1} {2} Cu^2(-\infin) = \frac {1} {2} Cu^2(t) Wc(t)=∫−∞tp(λ)d(λ)=21Cu2(t)−21Cu2(−∞)=21Cu2(t)
电感线圈(电感器)
一根导线当通有电流时,周围会产生磁场,若将
导线绕成线圈,可增加线圈内部磁场匝数: N 匝数:N 匝数:N
磁通: Φ : 每匝都会感应出磁通 磁通:\Phi: 每匝都会感应出磁通 磁通:Φ:每匝都会感应出磁通
磁链: Ψ = N Φ :匝与匝之间相互交链 磁链:\Psi = N \Phi:匝与匝之间相互交链 磁链:Ψ=NΦ:匝与匝之间相互交链
线性电感 L = Ψ i : 表征电感元件产生磁链能力的物理量 线性电感 L = \frac {\Psi} {i}: 表征电感元件产生磁链能力的物理量 线性电感L=iΨ:表征电感元件产生磁链能力的物理量
u ( t ) = d ψ d t u(t) = \frac {d\psi} {dt} u(t)=dtdψ
u = L d i d t u = L \frac {di} {dt} u=Ldtdi
W L ( t ) = ∫ − ∞ t p ( λ ) d λ = ∫ − ∞ t i L d i d λ d λ = 1 2 L i 2 ( t ) − 1 2 i 2 ( − ∞ ) W_L(t) = \int_{-\infin}^t p(\lambda)d\lambda = \int_{-\infin}^tiL \frac {di} {d\lambda}d\lambda = \frac {1} {2} Li^2(t) - \frac {1} {2} i^2 (-\infin) WL(t)=∫−∞tp(λ)dλ=∫−∞tiLdλdidλ=21Li2(t)−21i2(−∞)
W L ( t ) = 1 2 L i 2 ( t ) W_L(t) = \frac {1} {2} L i^2(t) WL(t)=21Li2(t)
三、正弦稳态电路分析
和
第一章的解题思路是一样的,多了个相量表示而已
正弦交流电的基本概念:
w = 2 Π T = 2 Π f w = \frac {2Π} {T} = 2Πf w=T2Π=2Πf
相位差: ψ = θ 1 − θ 2 相位差:\psi = \theta_1 - \theta_2 相位差:ψ=θ1−θ2
I = 0.707 I m I = 0.707I_m I=0.707Im
U = 0.707 U m U = 0.707U_m U=0.707Um
u = U m s i n ( w t + θ u ) u = U_msin(wt + \theta_u) u=Umsin(wt+θu)
i = I m s i n ( w t + θ i ) i = I_msin(wt + \theta_i) i=Imsin(wt+θi)
正弦量的向量表示
任何一个正弦量都可以用一个相应的旋转又向线段来表示,而有向线段可以用复数来表示,那么
正弦量也可以用复数来表示A = a + j b = r c o s θ + j r s i n θ 有向线段的实部为 a ,虚部为 b , 长度为 r , 与横轴的夹角为 θ A = a + jb = rcos\theta + jrsin\theta 有向线段的实部为a,虚部为b,长度为r,与横轴的夹角为\theta A=a+jb=rcosθ+jrsinθ有向线段的实部为a,虚部为b,长度为r,与横轴的夹角为θ
欧拉公式 : e j θ = c o s θ + j s i n θ = > A = r e j θ = r ∠ θ 欧拉公式: e^{j\theta} = cos\theta + jsin\theta => A = re^{j\theta} = r \angle \theta 欧拉公式:ejθ=cosθ+jsinθ=>A=rejθ=r∠θ
化简a = r c o s t θ a = rcost\theta a=rcostθ
b = r s i n θ b = rsin\theta b=rsinθ
r = a 2 + b 2 r = \sqrt{a^2 + b^2} r=a2+b2
θ = a r c t a n b a \theta = arctan \frac {b} {a} θ=arctanab
正弦量的复数称为相量⋅ U = U m ( c o s θ + j s i n θ ) = U m e j θ = U m ∠ θ {\cdot} {U} = U_m(cos\theta + jsin\theta) = U_me^{j\theta} = U_m \angle \theta ⋅U=Um(cosθ+jsinθ)=Umejθ=Um∠θ
⋅ i = I e j θ = i ∠ θ \cdot i = Ie^{j\theta} = i \angle \theta ⋅i=Iejθ=i∠θ
只有
同频率的正弦量可以画在同一个向量图上
基尔霍夫定律的向量表示
KCL: s u m i = 0 sum {i} = 0 sumi=0
KVL: s u m u = 0 sum u = 0 sumu=0
3种基本元件伏安关系的向量形式
电阻元件 R
⋅ U = R i ⋅ \cdot U = R i \cdot ⋅U=Ri⋅
电感元件 L
X L 称为感抗 = w L X_L称为感抗 = wL XL称为感抗=wL
U ⋅ = j w L i ⋅ = j X L i ⋅ U \cdot = jwLi\cdot = jX_Li\cdot U⋅=jwLi⋅=jXLi⋅L = j w L L = jwL L=jwL
电容元件 C
X c 称为容抗 = U I = 1 w C X_c称为容抗 = \frac {U} {I} = \frac {1} {wC} Xc称为容抗=IU=wC1
i ⋅ = j w C U ⋅ i\cdot = jwCU\cdot i⋅=jwCU⋅
C = 1 j w C C = \frac {1} {jwC} C=jwC1
简单正弦交流电路
RLC 串联交流电路
电阻端电压与电流同相,电感端电压超前电流90度,电容端电压滞后电流90度
U R = R I ⋅ , U L = j w L I = j X L I , U c = I ⋅ j W C = − j X c I ⋅ U_R = RI\cdot, U_L = jwLI=jX_LI,U_c = \frac {I\cdot}{jWC} = -jX_cI\cdot UR=RI⋅,UL=jwLI=jXLI,Uc=jWCI⋅=−jXcI⋅
公式推导:U ⋅ = U R ⋅ + U L ⋅ + U c ⋅ = ( R + j X L − j X c ) i ⋅ = ( R + j X ) I ⋅ = Z I ⋅ U\cdot = U_R \cdot + U_L \cdot + U_c \cdot = (R + jX_L - jX_c)i\cdot = (R+jX)I\cdot = ZI\cdot U⋅=UR⋅+UL⋅+Uc⋅=(R+jXL−jXc)i⋅=(R+jX)I⋅=ZI⋅
式中 , X = X L − X c = w L − 1 w C , X 称为电抗,单位为欧姆 ( Ω ) . 而 Z 称为复阻抗 Z = U ⋅ I ⋅ = R + j ( X L − X c ) = R = j X = ∣ Z ∣ ∠ Ψ 式中,X = X_L - X_c = wL - \frac {1} {wC}, X称为电抗,单位为欧姆(\Omega).而Z称为复阻抗 Z = \frac {U\cdot} {I\cdot} = R + j(X_L - X_c) = R = jX = \mid Z\mid \angle \Psi 式中,X=XL−Xc=wL−wC1,X称为电抗,单位为欧姆(Ω).而Z称为复阻抗Z=I⋅U⋅=R+j(XL−Xc)=R=jX=∣Z∣∠Ψ
模和辐射角为 ∣ Z ∣ = R 2 + X 2 = R 2 + ( w L − 1 w C ) 2 , Ψ = a r c t a n X R 模和辐射角为 \mid Z \mid = \sqrt{R^2 + X^2} = \sqrt{R^2 + (wL - \frac {1} {wC})^2},\Psi = arctan \frac {X} {R} 模和辐射角为∣Z∣=R2+X2=R2+(wL−wC1)2,Ψ=arctanRX
Z = U ⋅ I ⋅ = U I ∠ ( θ u − θ i ) , U I = ∣ Z ∣ , Ψ = θ u − θ i Z = \frac {U\cdot} {I\cdot} = \frac {U} {I} \angle{(\theta_u - \theta_i)}, \frac {U} {I} = \mid Z \mid, \Psi = \theta_u - \theta_i Z=I⋅U⋅=IU∠(θu−θi),IU=∣Z∣,Ψ=θu−θi
复阻抗模等于电压有效值与电路有效值之比,单位为欧姆
阻抗角等于电压与电流的相位差。
阻抗角的性质:X L > X c 时 , X > 0 , ψ > 0 , 电压超前电流 90 度,单路呈电感性,称为感性电路 X_L > X_c时, X > 0, \psi > 0,电压超前电流 90度,单路呈电感性,称为感性电路 XL>Xc时,X>0,ψ>0,电压超前电流90度,单路呈电感性,称为感性电路
X L < X c 时 , X < 0 , ψ < 0 , 电压滞后电流 90 度,电路呈电容性,称为容性电路 X_L < X_c时,X < 0, \psi < 0,电压滞后电流90度,电路呈电容性,称为容性电路 XL<Xc时,X<0,ψ<0,电压滞后电流90度,电路呈电容性,称为容性电路
X L = X c 时 , X = 0 , ψ = 0 , 电压与电流同相,电阻呈电阻性,称为电阻性电路 X_L = X_c时, X = 0, \psi = 0, 电压与电流同相,电阻呈电阻性,称为电阻性电路 XL=Xc时,X=0,ψ=0,电压与电流同相,电阻呈电阻性,称为电阻性电路
阻抗的串并连
阻抗的串联:等效阻抗与分压同普通电阻
阻抗的并联:等效阻抗与分流同普通电阻
导纳并联:复阻抗的倒数等效导纳与分流同普通电阻串联
正弦稳态电路的分析(必考)
将正弦稳态电路与直流电阻电路比较,若
正弦交流电路的各电压,电流用相量表示,电阻和电导用阻抗和导纳表示,则计算直流电阻电路的一些公式,分析方法及定律就可以完全用到正弦稳态的分析和计算中来
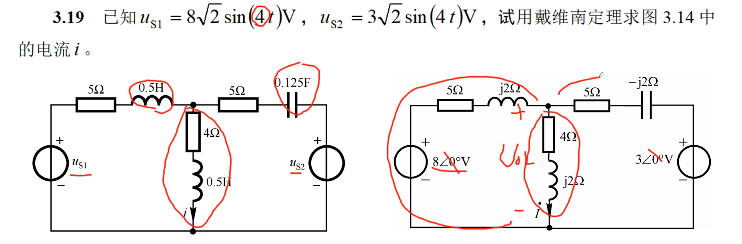
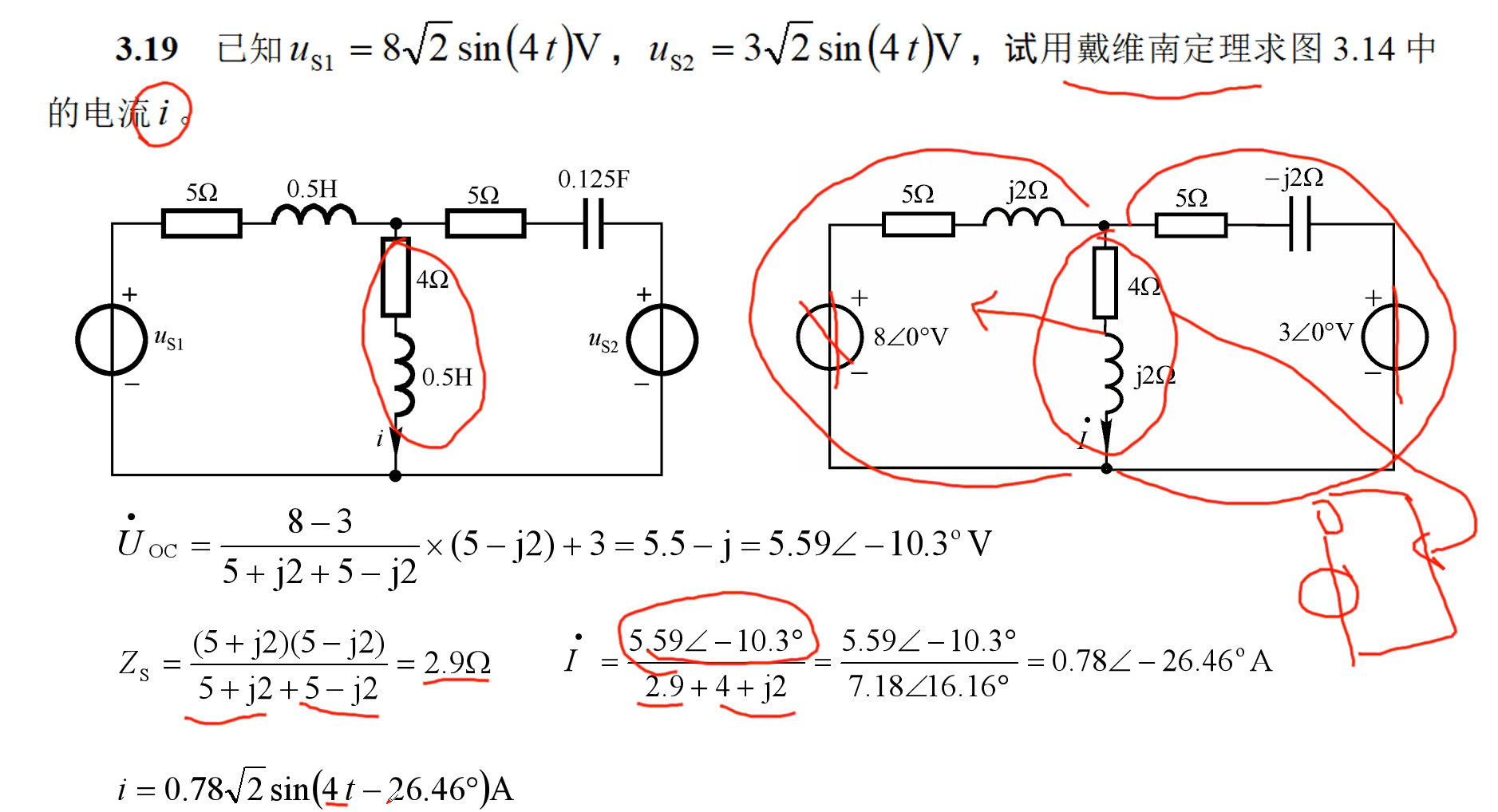
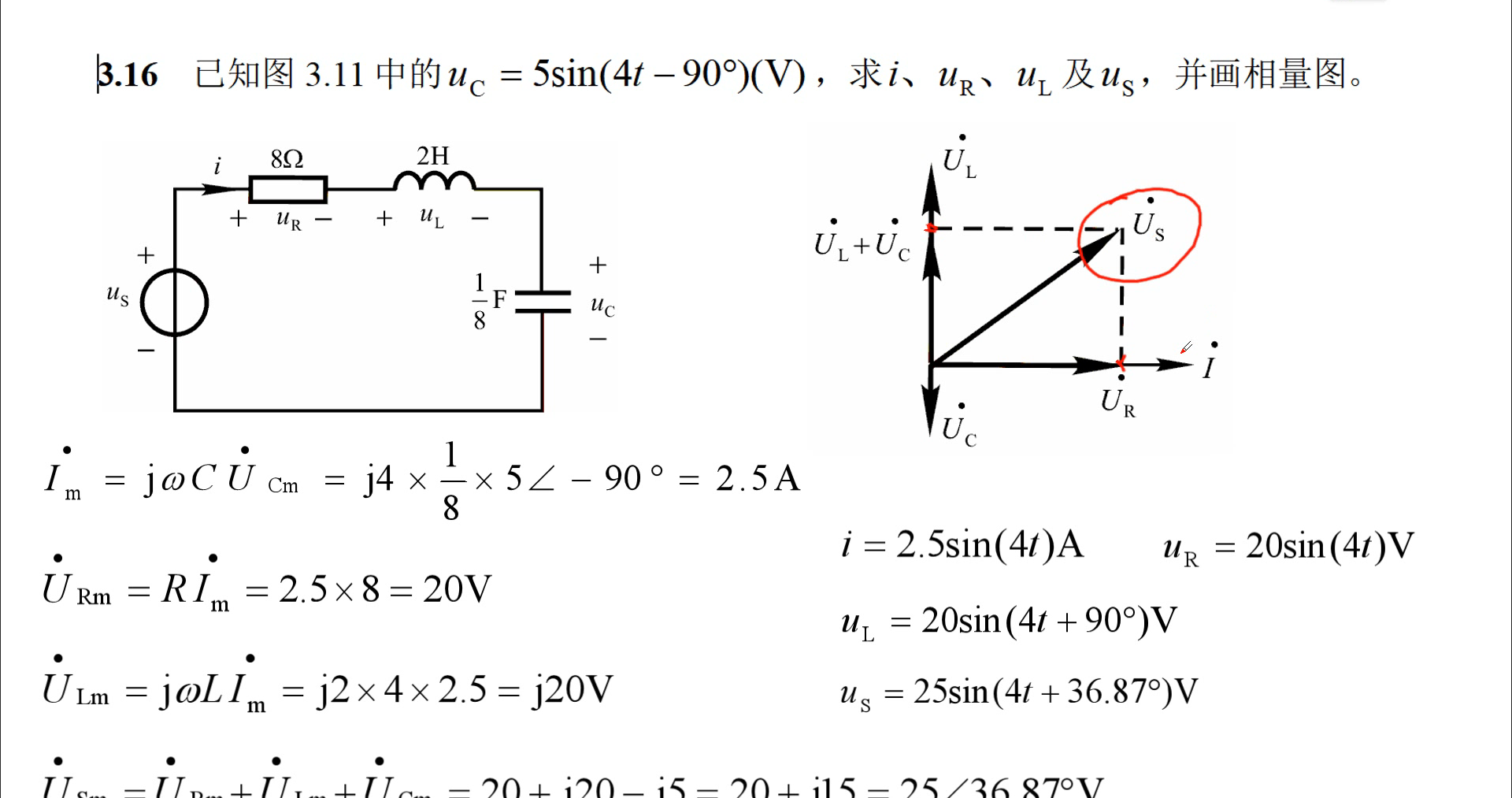
四、半导体二极管及直流稳压电源
知识总结
二极管的常见结构:
点接触型:结面积小,高频性能好,但允许通过的电流较小面接触型: 结面积大,可以通过较大的电流,工作频率较低硅平面型: 结面积大的可用于大功率整流,结面积小的适用于脉冲数字电路
二极管的伏安特性
正偏: P 区接电源的正级, N 区接电源的负极,也叫做PN结正向偏置反偏: P 区接电源的负极, N 区接电源的正极,也叫做PN结反向偏置正向特性: 只有在正向电压增大到足够大时,正向电流才从零开始随端电压按指数规律增大。临界电压称为开启电压,硅二极管开启电压约为 0.5V,锗开启电压为0.1V。当电流迅速增加时,二极管的正向压降却变化很小。定义这时二极管的管压降,称为正向导通压降。- PN结具有单向导电性。正向偏置时导通,反向偏置时截至
反向特性: 当反向电压增大到一定值时,反向电流会急剧增加,称为反向击穿,具有稳定电压的作用。反向击穿属于电击穿,电击穿过程在 PN 结被破坏之前是可逆的。因温度上升,直到过热而造成破坏性的击穿,称为热击穿。热击穿是不可逆的。- 根据半导体理论分析, P N 结的伏安特性方程近似为 i = I x ( e u U r − 1 ) 根据半导体理论分析,PN结的伏安特性方程近似为 i = I_x(e^{\frac {u} {U_r}} - 1) 根据半导体理论分析,PN结的伏安特性方程近似为i=Ix(eUru−1)
- u 为 P N 结的外加电压, i 为流过 P N 结的电流; T 是热力学温度; I s 是反向饱和电流; U T 是温度的电压当量, U T = k T q , q 为电子电荷量, k 是伯尔曼常数 , 常温下 , 即 T = 300 K 时 , U T = 26 m V u为PN结的外加电压,i为流过PN结的电流;T是热力学温度;I_s是反向饱和电流;U_T是温度的电压当量,U_T = \frac {kT} {q},q为电子电荷量,k 是伯尔曼常数,常温下,即 T = 300K时, U_T = 26mV u为PN结的外加电压,i为流过PN结的电流;T是热力学温度;Is是反向饱和电流;UT是温度的电压当量,UT=qkT,q为电子电荷量,k是伯尔曼常数,常温下,即T=300K时,UT=26mV
最大整流电流I: 二极管正向平均电流若超过此值,则将因为PN结温度上升过高而烧毁最高反向工作电压: 最高反向工作电压保证为击穿电压的一半,以确保二极管安全运行反向电流: 受温度影响较大,它越小说明二极管的单向导电性越好。最高工作频率: 是二极管的上限频率,超过此值,单向导电性能开始明显退化时的信号频率
晶体二极管电路的分析方法
简化电路模型
-
理想二极管模型(电源电压远比二极管的管压降大): 当外加正向电压时,二极管导通,正向压降为0V。外加反向电压时,二极管截止,认为它的电阻为无穷大,反向电流为0。 -
恒压降模型(近拟分析):二极管正向导通后,其管压降不随电流变化,认为是恒定值(硅管为0.7V,锗管取0.3V)并且二极管反向电流为零。 -
折线模型: 当二极管正向电压大于开启电压后,其电流与电压成线性关系,直线斜率为 1 / r。当二极管两端电压小于开启电压时,二极管截止,电流为零。 -
交流小信号等效模型: 交流小信号等效模型被用来计算 叠加在静态工作点上微小增量电压或电流的相应。二极管在静态工作点 Q 附近的电路模型为一个电阻,如图 5.2.4 ( c ) 所示。其中 r d = U T I D = 26 ( m V ) I D ( m A ) ( 室温下, T = 300 K 时 ) 二极管在静态工作点Q附近的电路模型为一个电阻,如图5.2.4(c)所示。其中 r_d = \frac {U_T} {I_D} = \frac {26(mV)} {I_D(mA)}(室温下,T = 300K 时) 二极管在静态工作点Q附近的电路模型为一个电阻,如图5.2.4(c)所示。其中rd=IDUT=ID(mA)26(mV)(室温下,T=300K时)
晶体二级管电路的分析方法(重点)
不同的模型,采用的分析方法也不同。已知电源V和电阻R,求二极管端电压U和流过的二极管的电流i
-
数值解法:U D = V D D − i D R , i D = I s ( e u D U T − 1 ) 联立可解得 : U D , I D U_D = V_{DD} - i_DR, i_D = I_s(e^{\frac {u_D} {U_T}} - 1)联立可解得: U_D, I_D UD=VDD−iDR,iD=Is(eUTuD−1)联立可解得:UD,ID
-
图解分析法(不实用):U D = V D D − i D R 对应的是一条直线,称为负载线。其与二极管伏安特性曲线的交点 Q 的坐标值 ( U D , I D ) 便是所需求得解。 Q 点称为电路得工作点 U_D = V_{DD} - i_DR对应的是一条直线,称为负载线。其与二极管伏安特性曲线的交点Q的坐标值(U_D, I_D)便是所需求得解。Q点称为电路得工作点 UD=VDD−iDR对应的是一条直线,称为负载线。其与二极管伏安特性曲线的交点Q的坐标值(UD,ID)便是所需求得解。Q点称为电路得工作点
-
简化模型分析法: 利用上小节知识点对题目进行解答
实战演练

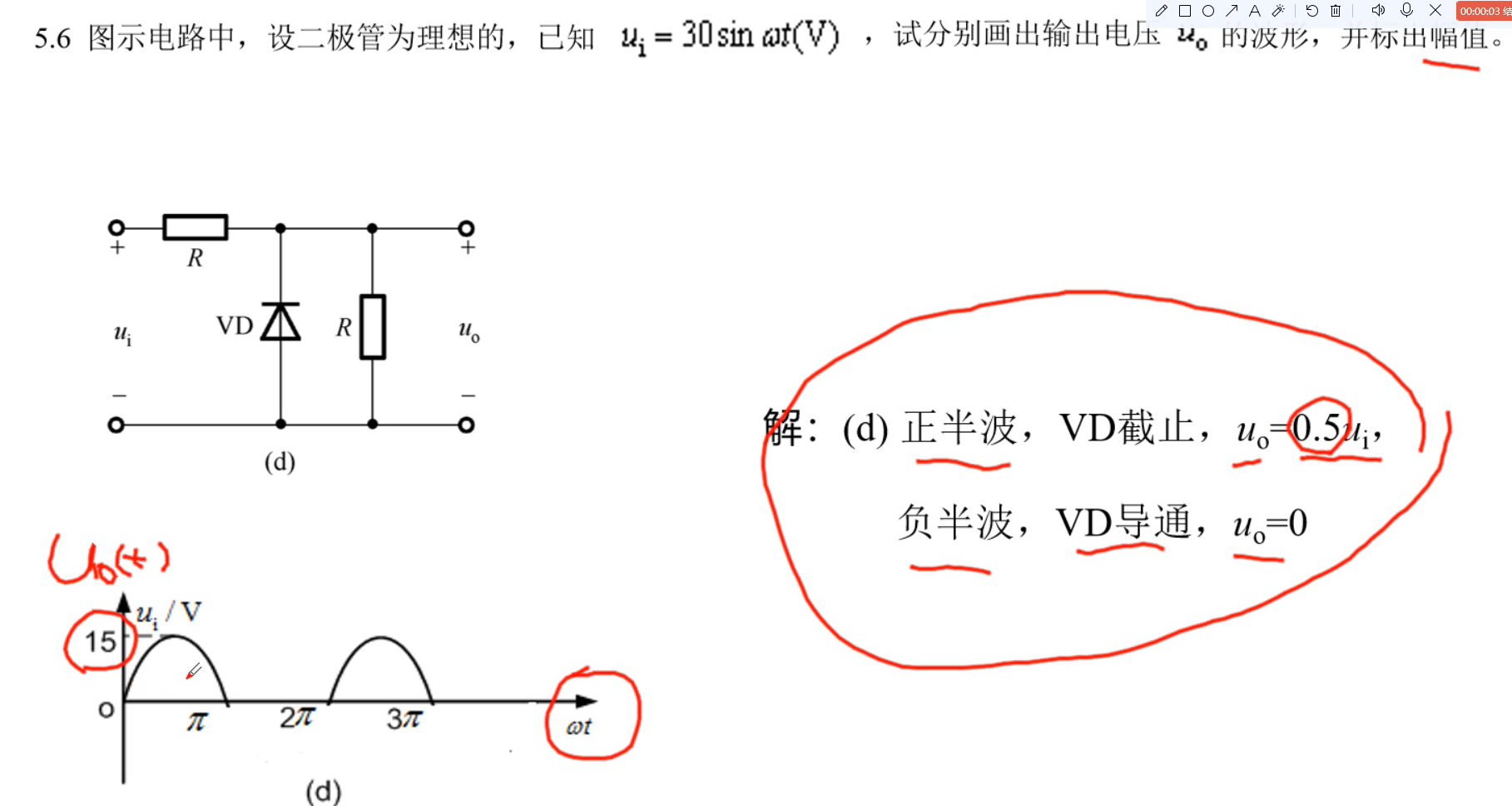
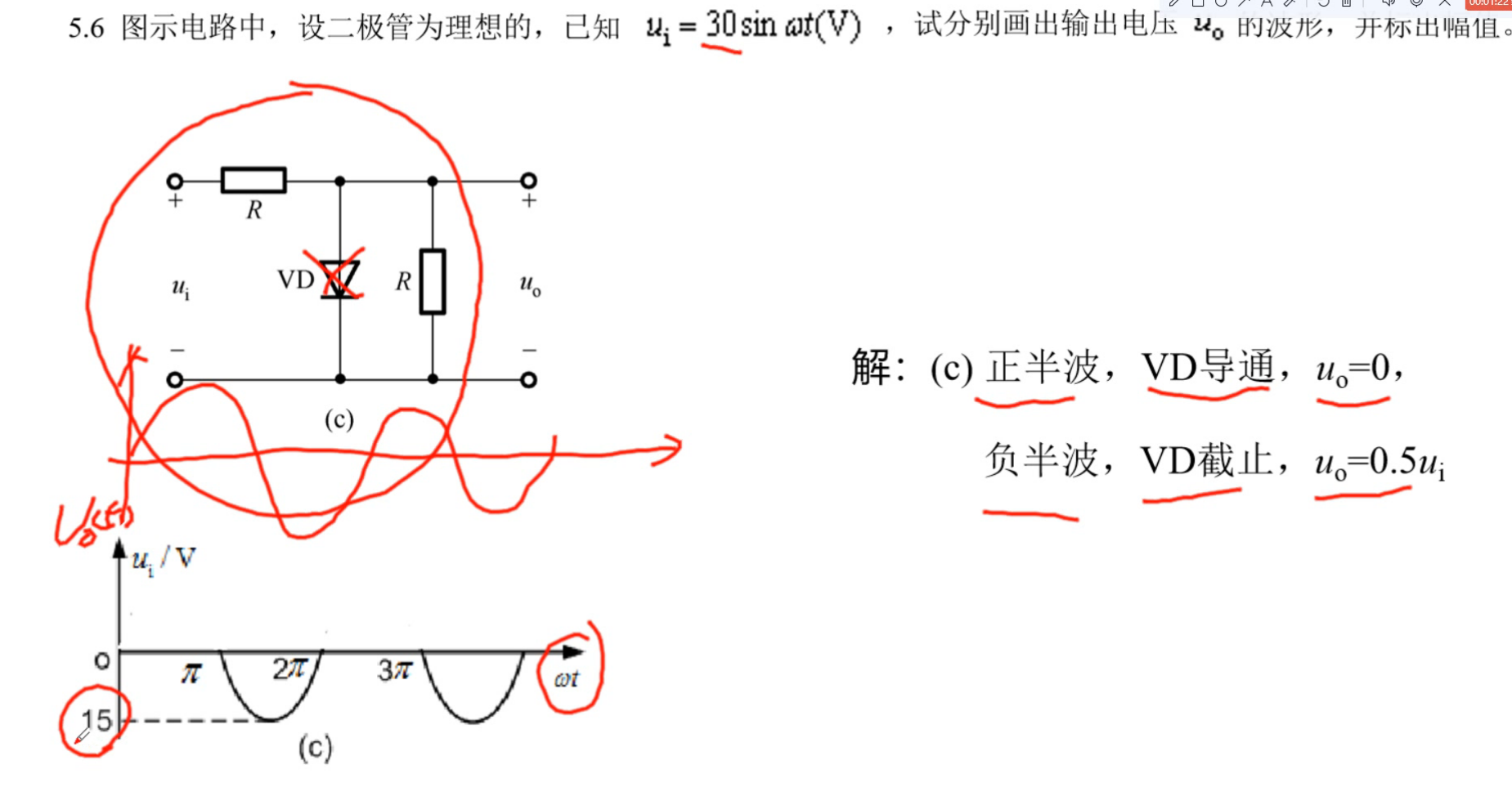
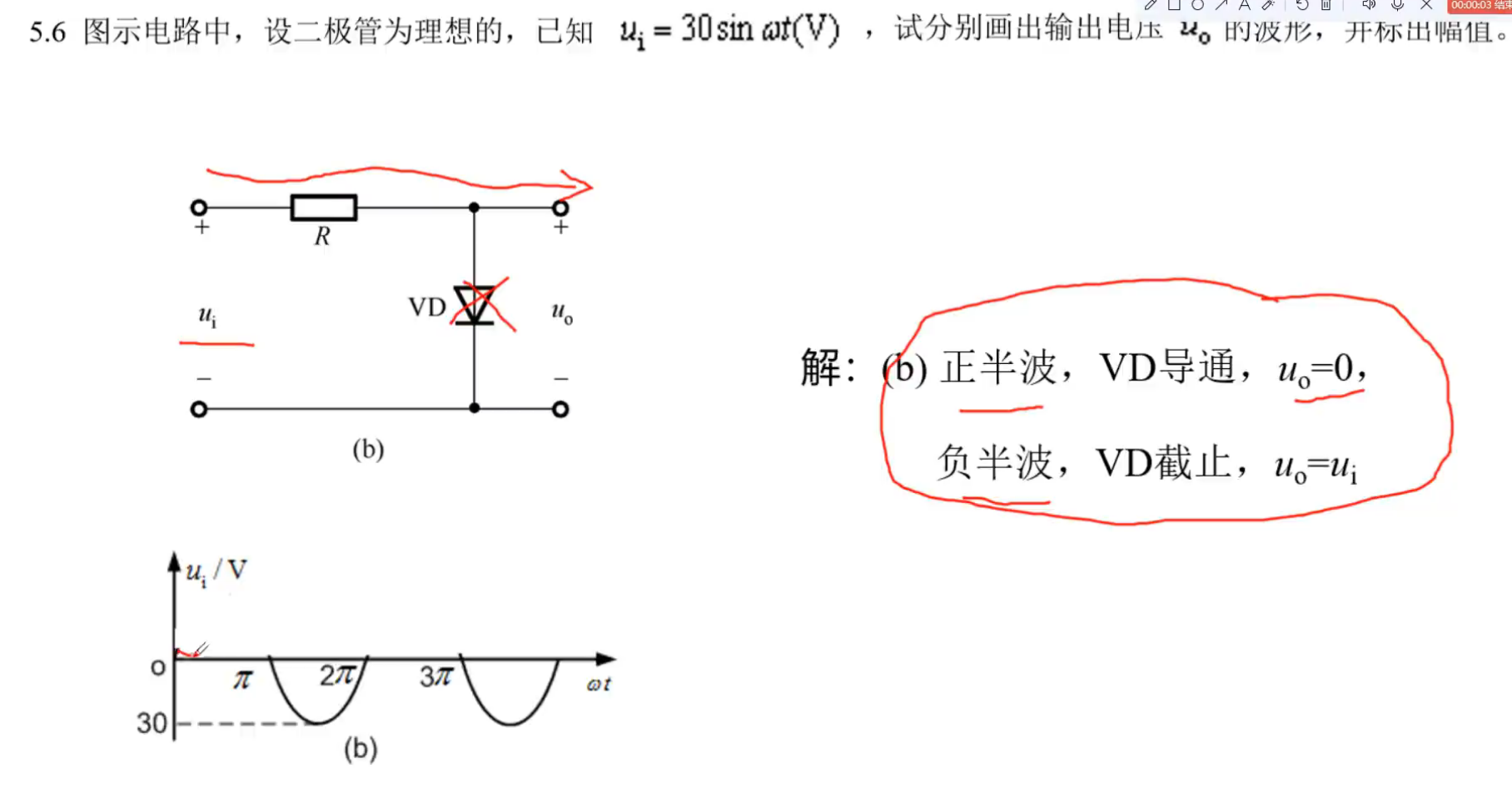
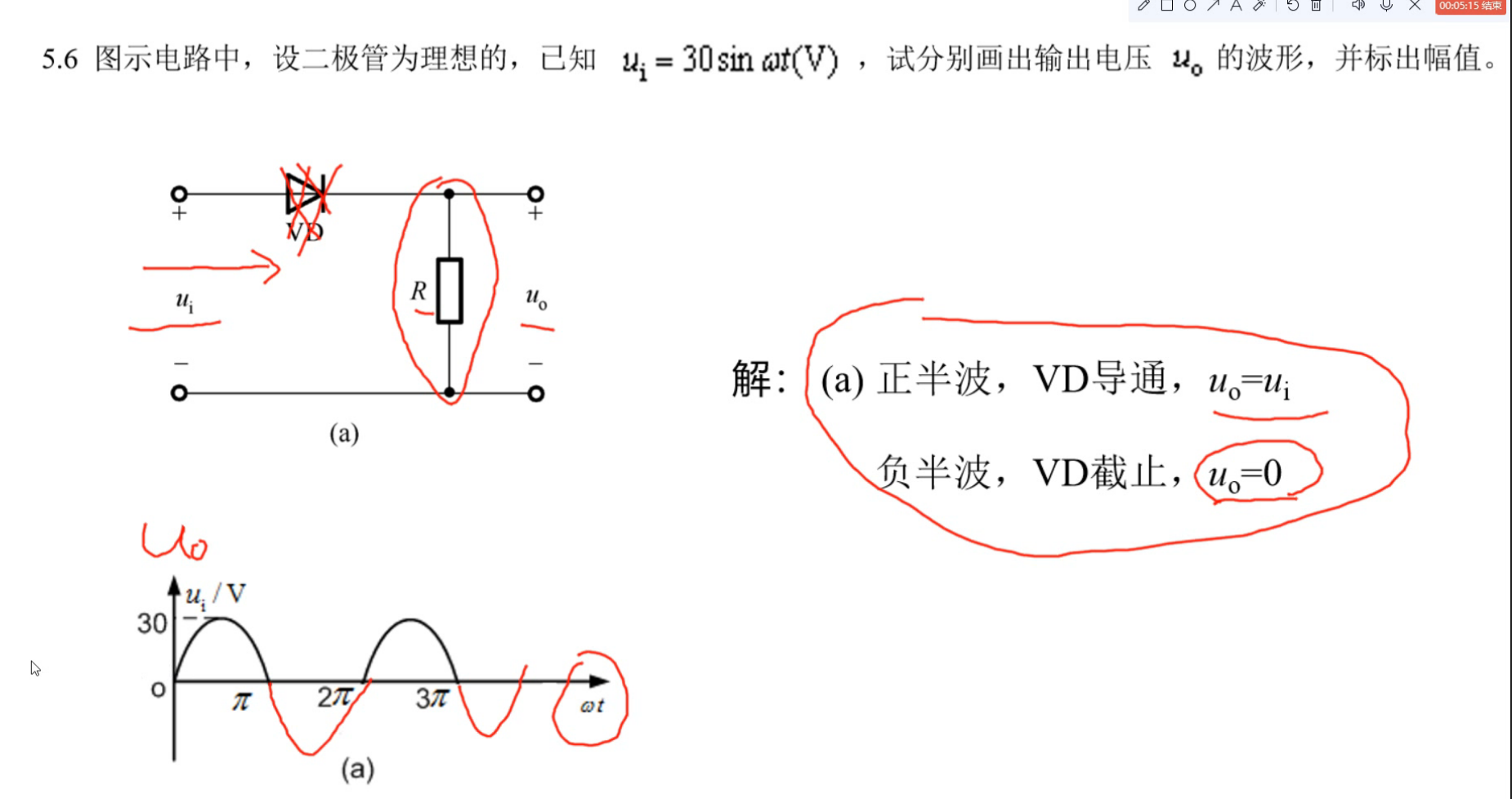
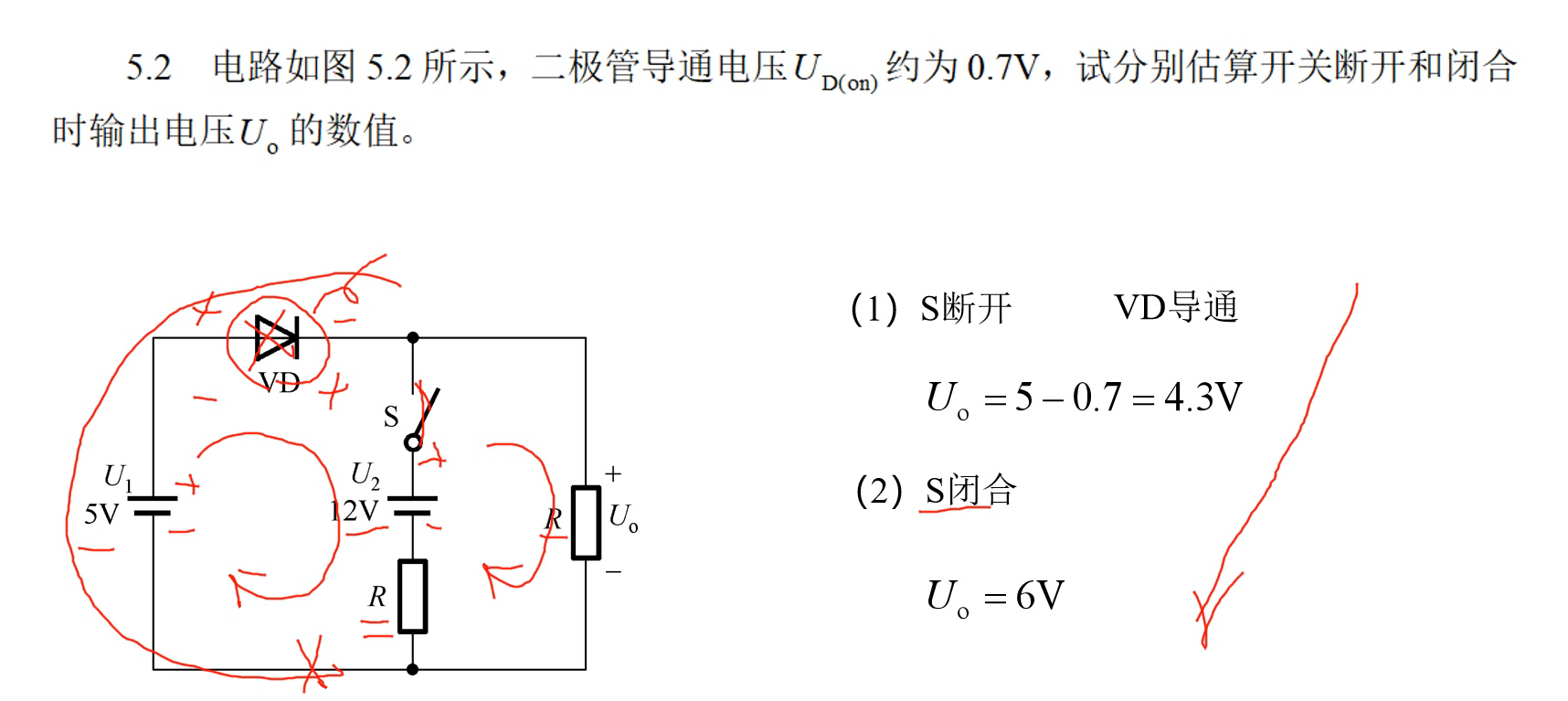
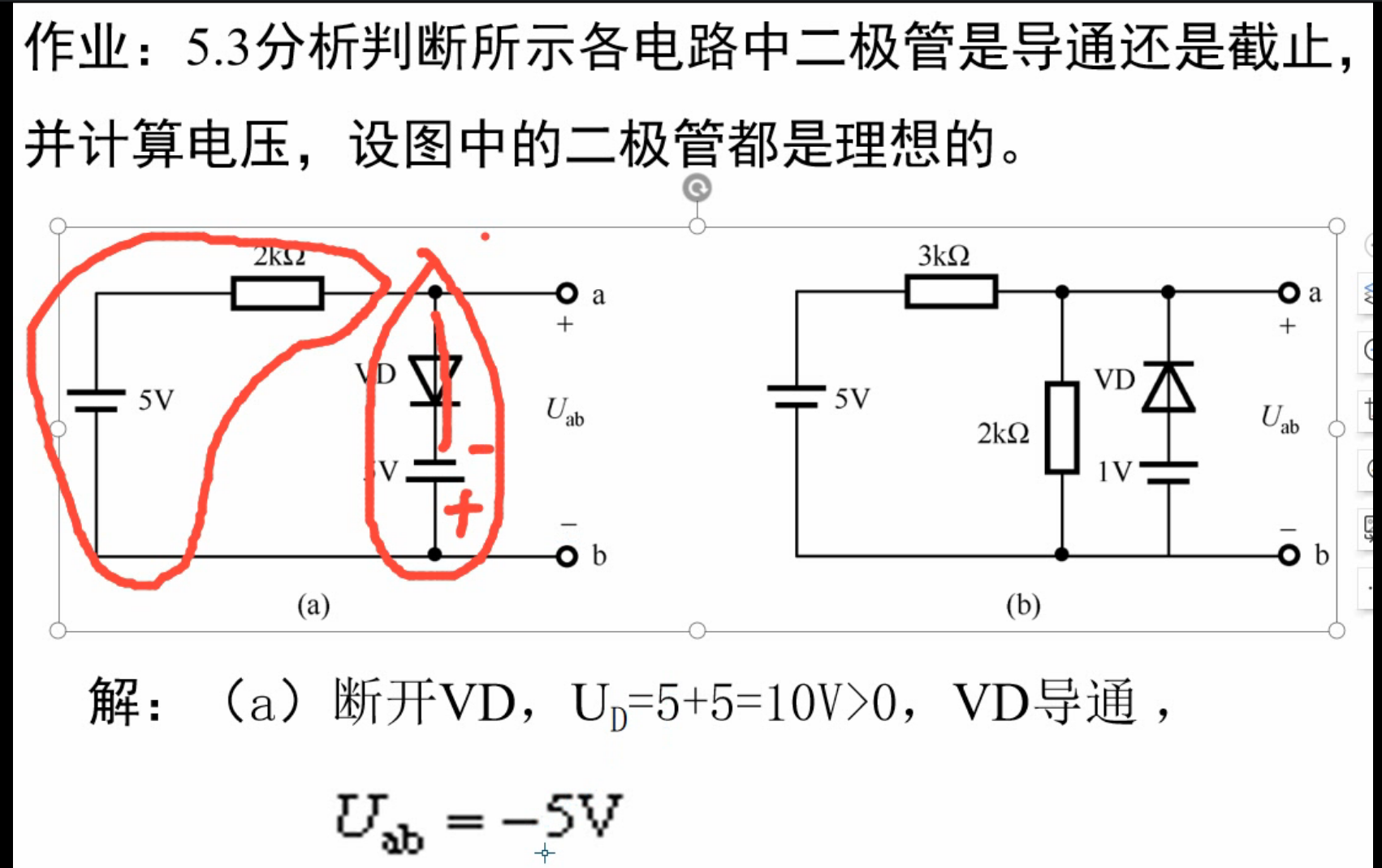
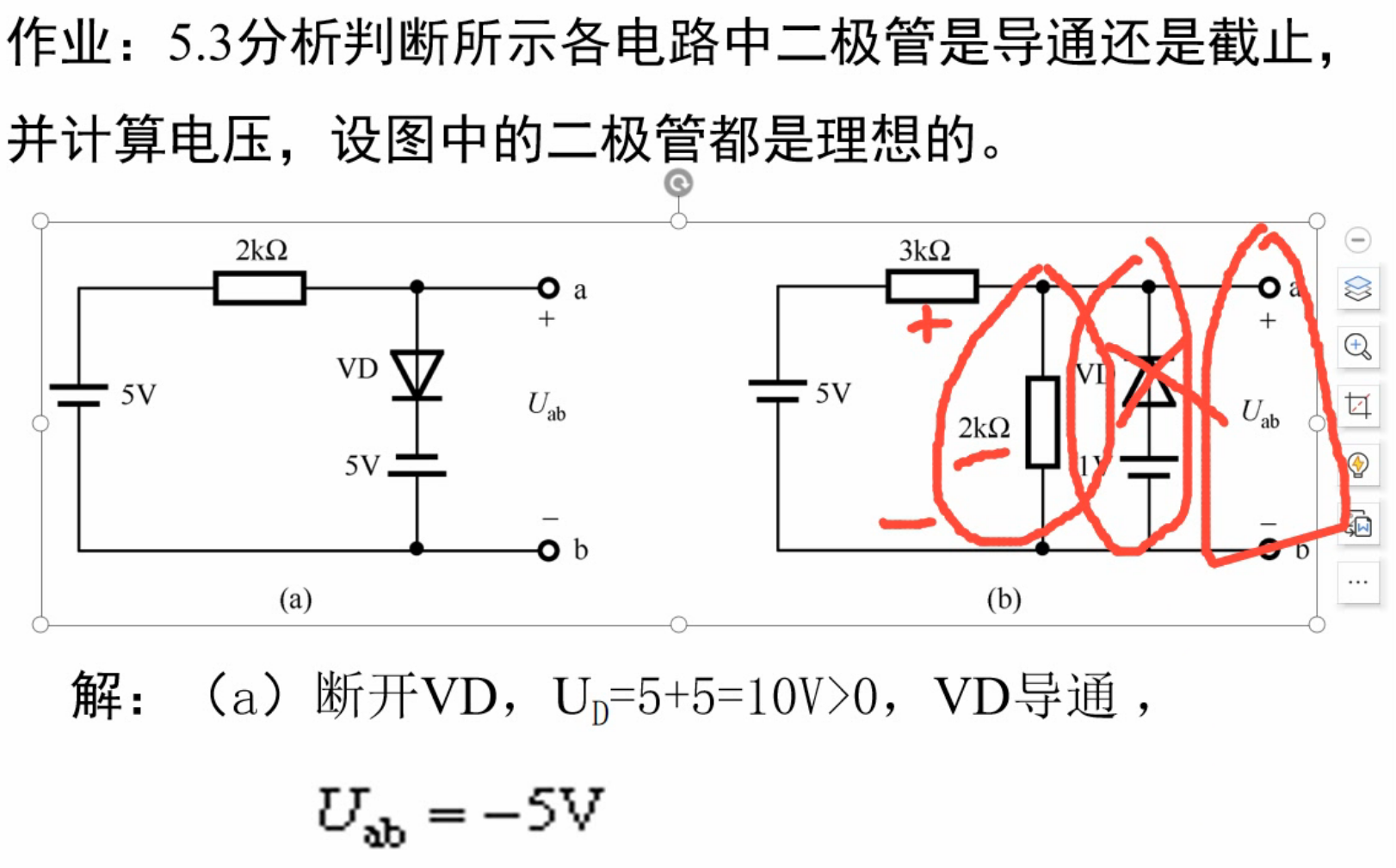
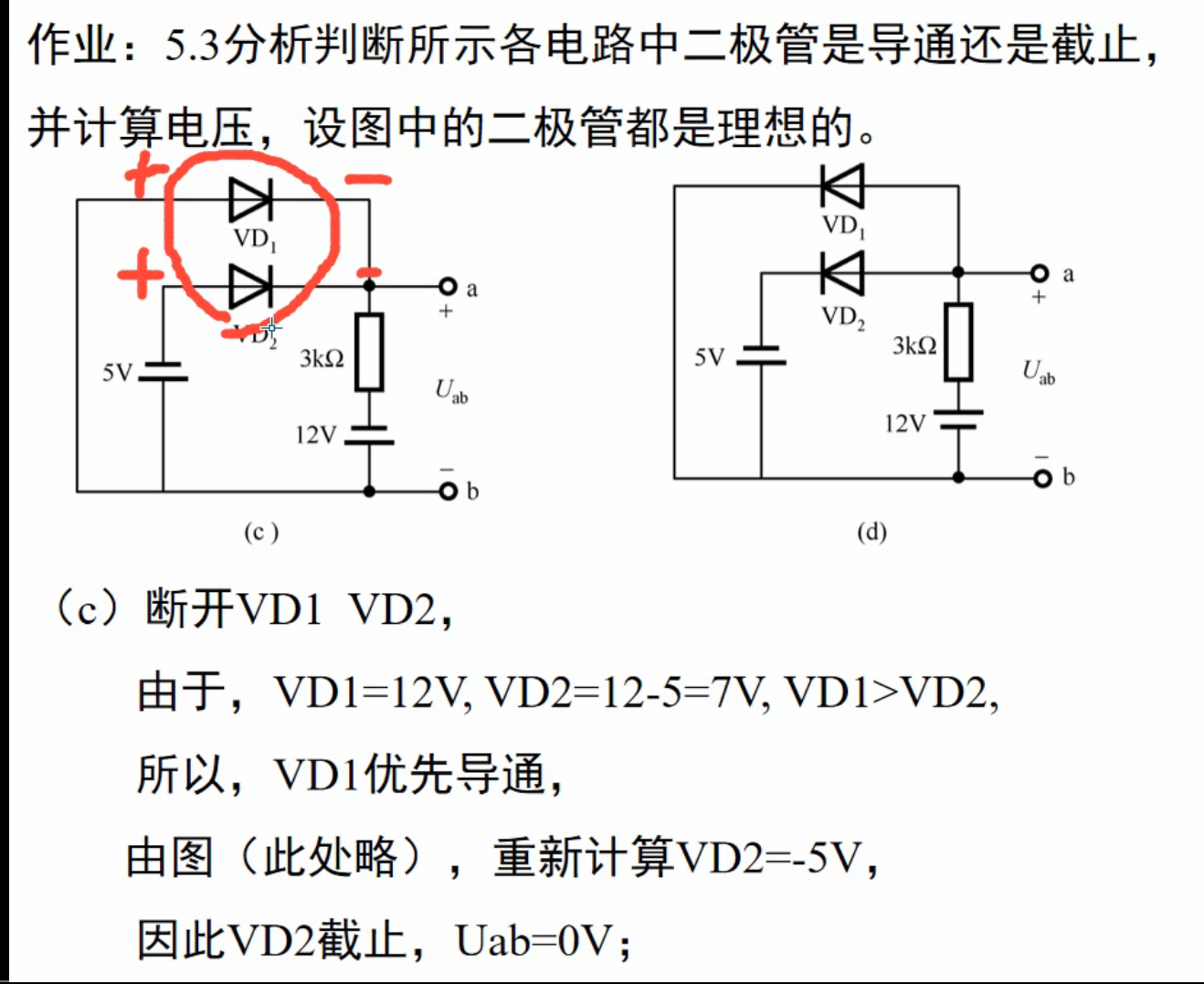
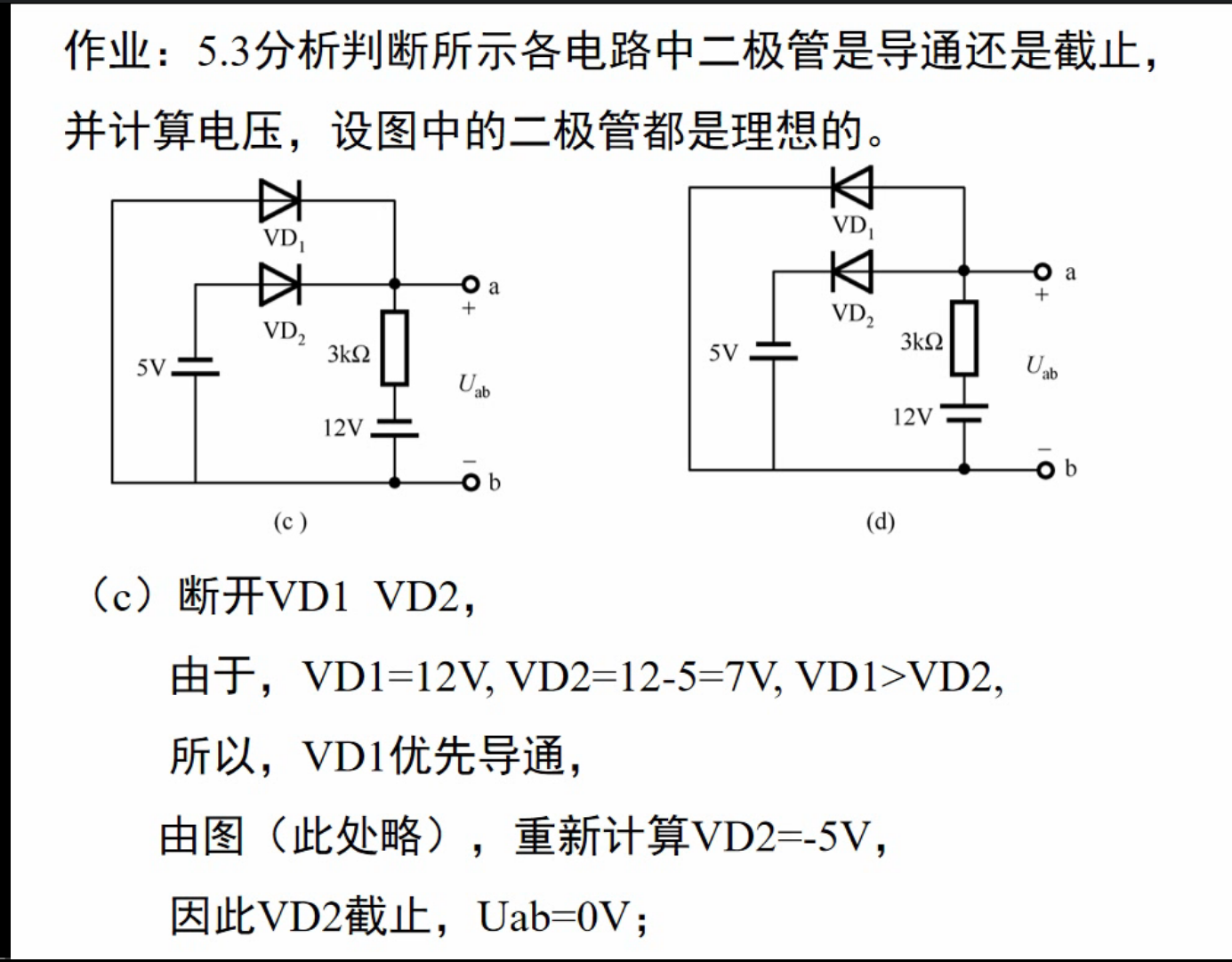
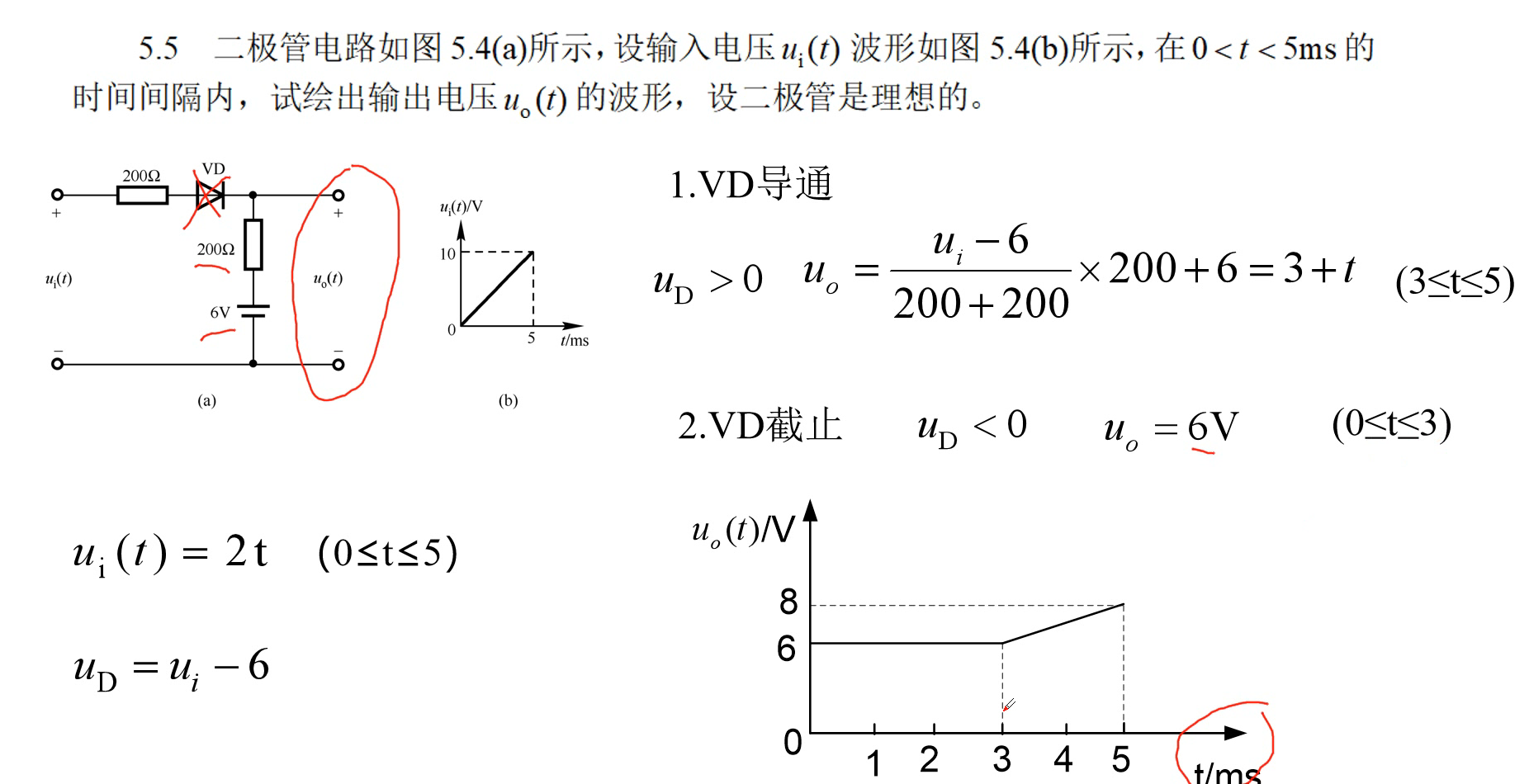
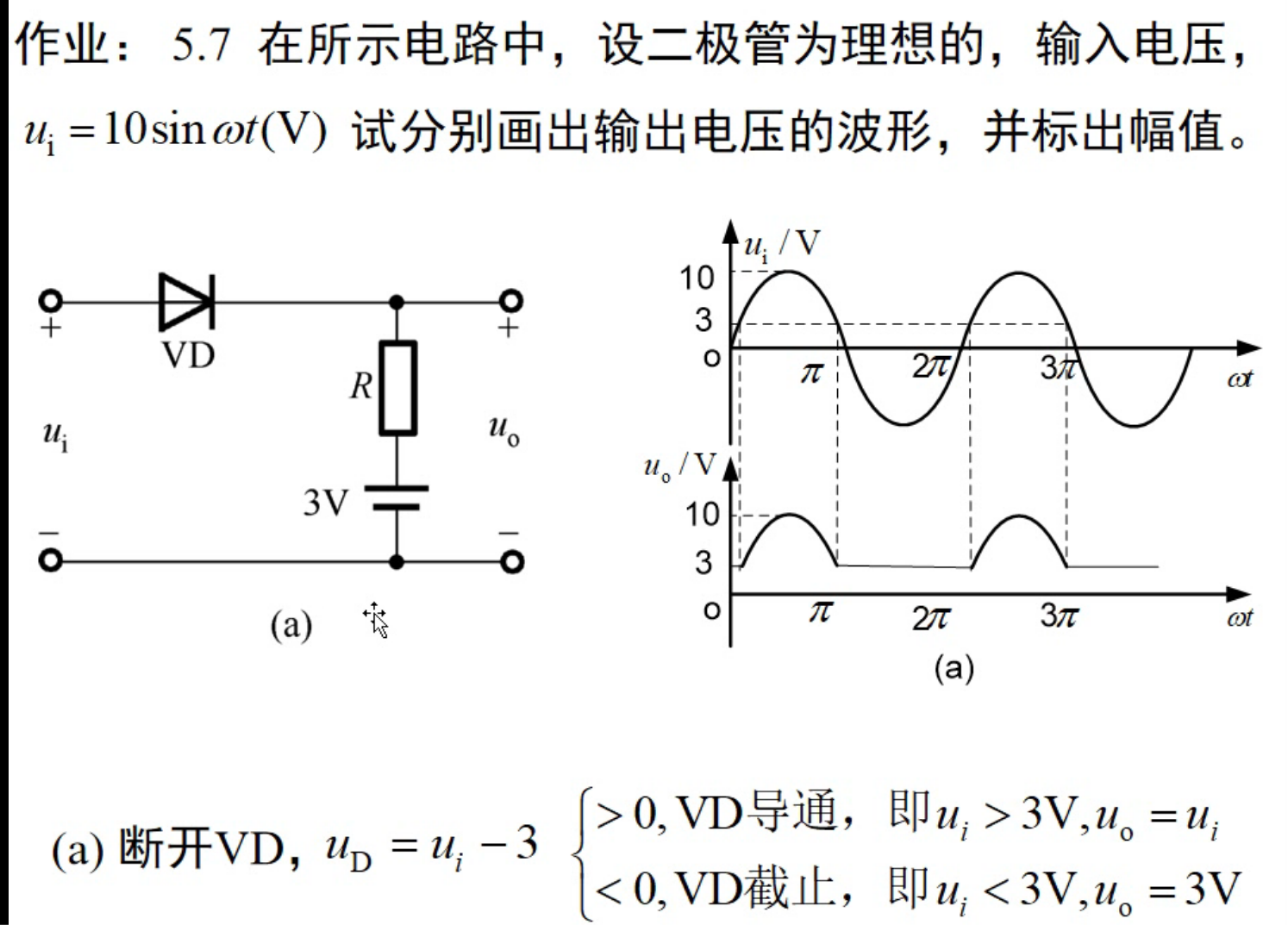
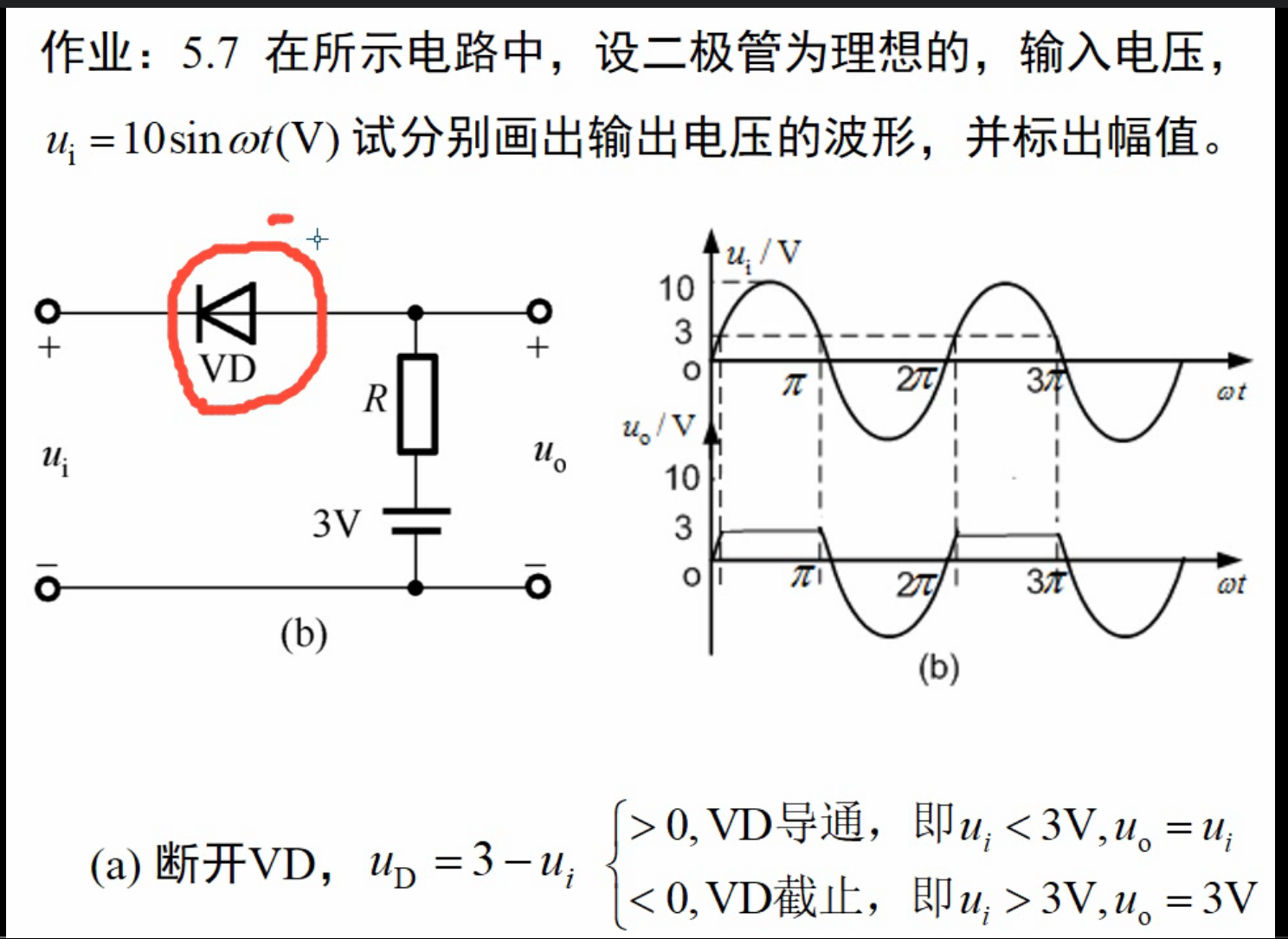
五、晶体三极管及其放大电路
晶体三级管的外部特性
晶体管的类型及符号
使用不同杂志掺杂得到一个 P 区和两个 N 区,并形成两个 PN 结,分别用引线连接 3 个区域。对应的电极分别称为 发射极(emitter),基极(base),和集电极(collector)
三极管分类:
- 工艺分类:
有 NPN 和 PNP 型- 制造材料分类:锗管和硅管
- 按照工作频率分类:低频管和高频管
- 容许耗散功率大小分类:小功率管和大功率管
晶体管的电流分配与放大作用
使晶体管工作在
放大状态的外部条件是发射结正向偏置且集电结反向偏置。N P N 管,应该使得 V B > V E , V C > V B , V B B 使得发射结正偏 , V c c 使得集电结反偏 I E = I C + I B NPN管,应该使得 V_B > V_E, V_C > V_B, V_{{BB}}使得发射结正偏, V_{cc}使得集电结反偏 I_E= I_C + I_B NPN管,应该使得VB>VE,VC>VB,VBB使得发射结正偏,Vcc使得集电结反偏IE=IC+IB
发射极电流是电路中
最大的电流,集电极电流稍小,基极电流很小。从基极到集电极的电流增益是基本确定的,称为特征值β ‾ ≈ I c I B \overline \beta \approx \frac {I_c} {I_B} β≈IBIc
晶体管的共射特性曲线
输入回路: 电源 V B B 和电阻 R b 接入基极 电源V_{BB}和电阻R_b接入基极 电源VBB和电阻Rb接入基极
输出回路: 电源 V c c 和电阻 R c 在集电极 电源V_{cc}和电阻R_c在集电极 电源Vcc和电阻Rc在集电极
共射电路: 发射极是两个回路的公共端
输入特性曲线:
死区电压: 发射结外加电压大于死区电压时,晶体管才会出现iB硅管的死区电压约为0.5V,锗管的死区电压约为0.1V- N P N 型硅管的发射结电压 U B E 为 0.6 ≈ 0.7 V , 锗管的发射结电压 U B E 为 0.2 V ≈ 0.3 V NPN型硅管的发射结电压U_{BE}为 0.6 \approx 0.7V,锗管的发射结电压U_{BE}为0.2V \approx 0.3V NPN型硅管的发射结电压UBE为0.6≈0.7V,锗管的发射结电压UBE为0.2V≈0.3V
- P N P 型,硅管的发射结电压 U B E 为 − 0.6 V ≈ − 0.7 V , 锗管的发射结电压 U B E 为 − 0.2 ≈ − 0.3 V PNP型,硅管的发射结电压U_{BE}为 -0.6V \approx -0.7V,锗管的发射结电压U_{BE}为-0.2 \approx -0.3V PNP型,硅管的发射结电压UBE为−0.6V≈−0.7V,锗管的发射结电压UBE为−0.2≈−0.3V
输出特性曲线:
截止区
晶体管工作在截止区时
没有电流放大能力,截止时发射结和集电结均反偏,且各极电流近视为零。I B = 0 时,集电极用 I C E O 表示,其值很小,即在截止区 , 电流关系为 I B = 0 , I E = I C = I C E O ,各极电流近似为零 I_B = 0时,集电极用I_{CEO}表示,其值很小,即在截止区,电流关系为I_{B} = 0, I_{E} = I_{C} = I_{CEO},各极电流近似为零 IB=0时,集电极用ICEO表示,其值很小,即在截止区,电流关系为IB=0,IE=IC=ICEO,各极电流近似为零
N P N 型硅管而言,当 u B E < 0.5 V 时,已开始截止 , 但是为了可靠截止 , 常使得 u B E < = 0 , 即截止时发射结和集电结均反偏 NPN型硅管而言,当u_{BE} < 0.5V时,已开始截止,但是为了可靠截止,常使得 u_{BE} <= 0,即截止时发射结和集电结均反偏 NPN型硅管而言,当uBE<0.5V时,已开始截止,但是为了可靠截止,常使得uBE<=0,即截止时发射结和集电结均反偏
放大区
i C = β i B , i E = i B + i C = ( 1 + β ) i B ≈ β i B , 表现出 i B 对 i C 的控制作用 i_C = \beta i_B, i_E = i_B + i_C = (1 + \beta)i_B \approx \beta i_B, 表现出i_B对i_C的控制作用 iC=βiB,iE=iB+iC=(1+β)iB≈βiB,表现出iB对iC的控制作用
当晶体管在放大状态时,
发射结正偏,集电结反偏。N P N 型晶体管而言,应使 U B E = U B E ( o n ) , U B C < 0 , 从电位来看,应该是 V C > V B > V E NPN型晶体管而言,应使U_{BE} = U_{BE(on)}, U_{BC} < 0,从电位来看,应该是V_C > V_B > V_E NPN型晶体管而言,应使UBE=UBE(on),UBC<0,从电位来看,应该是VC>VB>VE
P N P 型晶体管而言,则是 V E > V B > V C PNP型晶体管而言,则是V_E > V_B > V_C PNP型晶体管而言,则是VE>VB>VC
饱和区
对应于不同 i B 的输出特性曲线几乎重合, i C 不再受 i B 控制,只随 U C E 变化,即没有电流放大能力 对应于不同i_B的输出特性曲线几乎重合,i_C不再受i_B控制,只随U_{CE}变化,即没有电流放大能力 对应于不同iB的输出特性曲线几乎重合,iC不再受iB控制,只随UCE变化,即没有电流放大能力
饱和时,
发射结与集电结均处于正向偏置。在饱和状态时的 U C E 称为饱和压降,记作 U C E S 对于 N P N 型硅管约为 0.3 V , P N P 型锗管约为 − 0.1 V 在饱和状态时的U_{CE}称为饱和压降,记作U_{CES} 对于 NPN 型硅管约为 0.3V, PNP型锗管约为-0.1V 在饱和状态时的UCE称为饱和压降,记作UCES对于NPN型硅管约为0.3V,PNP型锗管约为−0.1V
放大电路的组成和工作原理(了解)
一、放大电路器件工作在放大状态
二、放大的信号通路应通畅,即输入信号能送到放大电路的输入端
放大电路的分析(重点)
静态是当放大电路没有输入信号时的工作状态 : 要确定放大电路的静态工作点 Q ( I B Q , I C Q , U C E O ) 静态是当放大电路没有输入信号时的工作状态: 要确定放大电路的静态工作点Q(I_{BQ}, I_{CQ}, U_{CEO}) 静态是当放大电路没有输入信号时的工作状态:要确定放大电路的静态工作点Q(IBQ,ICQ,UCEO)
动态是有输入信号时的工作状态 : 确定放大电路的电压放大倍数 A u , 输入电阻 R i 和输出电阻 R o 等 动态是有输入信号时的工作状态: 确定放大电路的电压放大倍数A_{u},输入电阻R_i和输出电阻R_o等 动态是有输入信号时的工作状态:确定放大电路的电压放大倍数Au,输入电阻Ri和输出电阻Ro等
静态分析讨论的对象是直流成分,动态分析讨论的是交流成分,因此也可将此过程看成是叠加原理在放大电路中的应用
直流通路与交流通路
直流通路: 放大电路中直流流过的路径 交流输入信号置零,同时电容对直流有隔断作用,应将电容视为开路。交流通路: 放大电路中交流电流流过的路径 将直流电源置零,当电容值足够大,交流信号在电容上的压降可以忽略时,可将电容视为短路
静态分析
放大电路的直流通路
- 静态时基极电流为 I B Q = V c c − U B E Q R b 静态时基极电流为 I_{BQ} = \frac { V_{cc} - U_{BEQ}} {R_b} 静态时基极电流为IBQ=RbVcc−UBEQ
- U B E Q 常被认为是已知量 , 硅管约为 ( 0.6 V ≈ 0.7 V ) V ,锗管约为 ( 0.2 V ≈ 0.3 ) V U_{BEQ}常被认为是已知量,硅管约为(0.6V \approx 0.7V)V,锗管约为 (0.2V \approx 0.3)V UBEQ常被认为是已知量,硅管约为(0.6V≈0.7V)V,锗管约为(0.2V≈0.3)V
- I B Q 可求出静态时的集电极电流 I C Q = β I B Q I_{BQ}可求出静态时的集电极电流 I_{CQ} = \beta I_{BQ} IBQ可求出静态时的集电极电流ICQ=βIBQ
- 由集电极 − 发射极回路求 U C E Q = V c c − I C Q R c 由集电极-发射极回路求U_{CEQ} = V_{cc} - I_{CQ}R_c 由集电极−发射极回路求UCEQ=Vcc−ICQRc
图解法确定静态值
-
画出直流通路
-
利用输入特性曲线来确定 利用输入特性曲线来确定 利用输入特性曲线来确定
U B E = V B B − i B R b U_{BE} = V_{BB} - i_BR_b UBE=VBB−iBRb
-
可得回路方程 u C E = V c c − i c R c 可确定 I C Q 和 U C E Q 可得回路方程 u_{CE} = V_{cc} - i_c R_c 可确定I_{CQ}和U_{CEQ} 可得回路方程uCE=Vcc−icRc可确定ICQ和UCEQ
动态分析(放弃,建议彻底弄懂以上部分(肯定能过的))
微变等效电路法
把非线性元件晶体管所组成的放大电路等效为一个线性电路,也就是吧晶体管线性化,等效为一个线性元件
图解法
图解法分析放大电路的非线性失真和动态范围