【可解释性机器学习】基于SHAP进行特征选择和贡献度计算

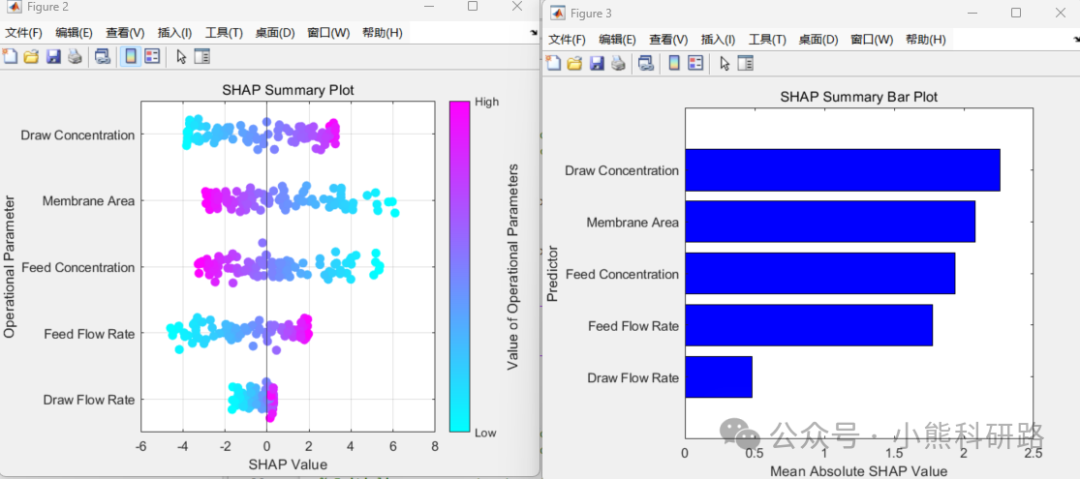
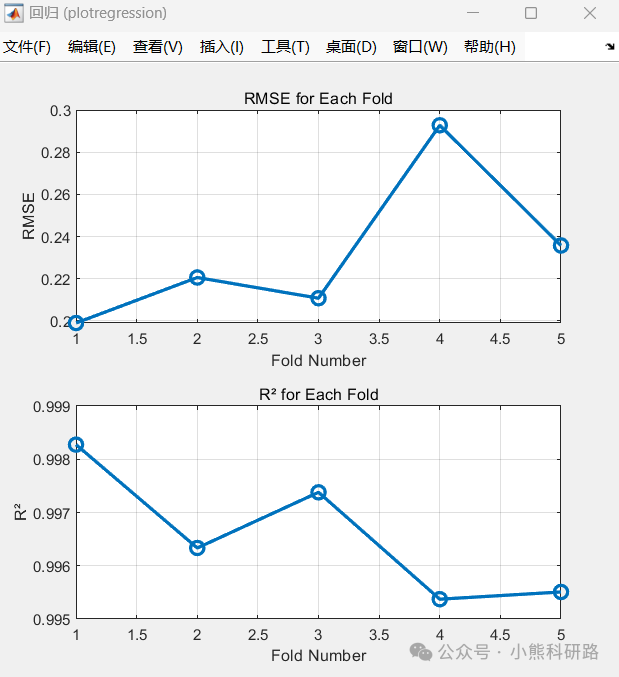
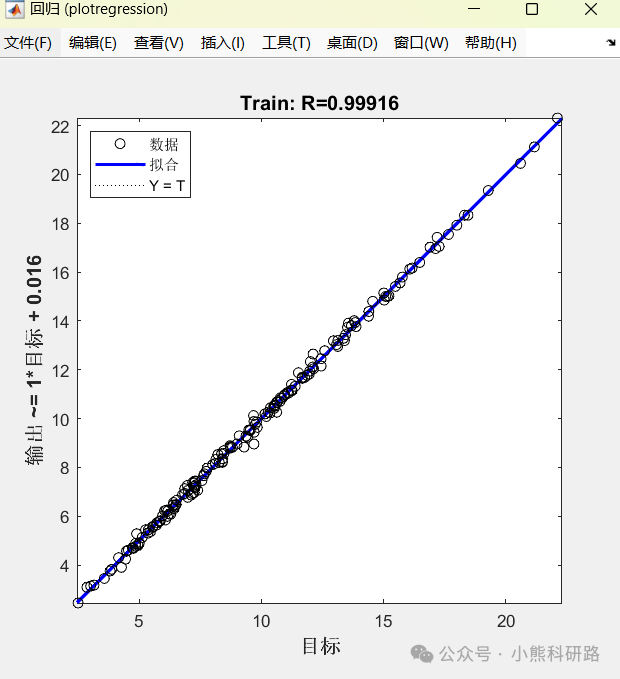
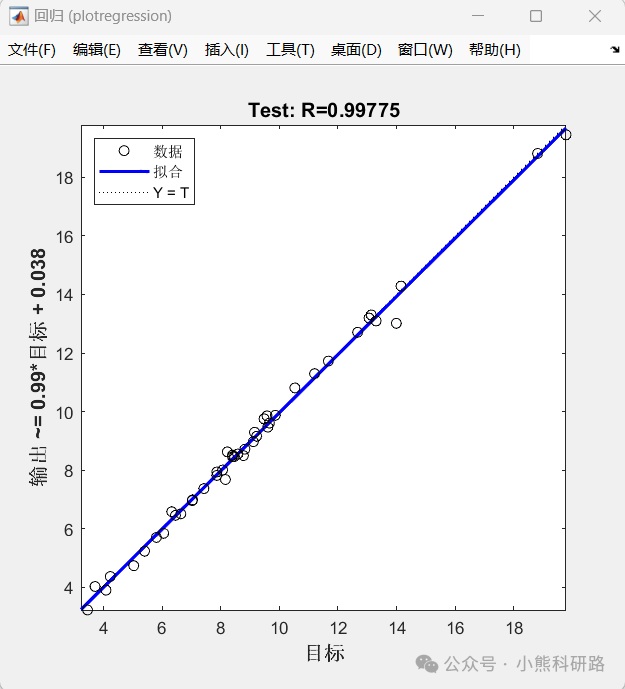
本文采用MATLAB编写了利用径向基函数神经网络（RBFNN采用五折交叉验证）实现了一个SHAP可解释的神经网络回归模型，用于预测正向渗透过程中的水通量。该模型利用操作参数，如膜面积，进料和提取溶液的流速和浓度作为训练的输入特征。为了提高可解释性，应用了SHapley加性解释（SHAP），允许用户深入了解每个参数对模型预测的贡献。为希望开发准确透明的回归模型的研究人员和工程师提供了强大的解决方案。

SHAP（SHapley Additive exPlanations）旨在解释任何机器学习模型的输出。SHAP 的名称源自合作博弈论中的 Shapley 值，它构建了一个加性的解释模型，将所有特征视为“贡献者”。对于每个预测样本，模型会产生一个预测值，而 SHAP 值则表示该样本中每个特征的贡献度。

文章可解释性机器学习_Feature Importance、Permutation Importance、SHAP中SHAP模型，是比较全能的模型可解释性的方法，既可作用于之前的全局解释，也可以局部解释，即单个样本来看，模型给出的预测值和某些特征可能的关系，这就可以用到SHAP。

SHAP 属于模型事后解释的方法，它的核心思想是计算特征对模型输出的边际贡献，再从全局和局部两个层面对“黑盒模型”进行解释。SHAP构建一个加性的解释模型，所有的特征都视为“贡献者”。

对于每个预测样本，模型都产生一个预测值，SHAP value就是该样本中每个特征所分配到的数值。

基本思想：计算一个特征加入到模型时的边际贡献，然后考虑到该特征在所有的特征序列的情况下不同的边际贡献，取均值，即某该特征的SHAPbaseline value.

假设第i个样本为Xi，第i个样本的第j个特征为Xij，模型对该样本的预测值为yi，整个模型的基线（通常是所有样本的目标变量的均值）为 ybase，那么 SHAP 值服从以下等式：

yi=ybase+f(Xi1)+f(Xi2)+⋯+f(Xik)

其中, f(Xij)表示第i个样本中第j个特征的 SHAP 值。从直观上看，f(Xi1)表示第i个样本中第1个特征对最终预测值yi的贡献。当f(Xj1)>0时，说明该特征提升了预测值，有正向作用；反之，则说明该特征降低了预测值，有反向作用。

运行效果和数据样本展示：

本文采用Matlab编写代码，代码注释详细，逻辑清晰易懂，数据采用excel表格形式便于替换数据集，可main函数一键运行。