数学建模启发式算法篇（一）---遗传算法

1.引言

最近在准备本月亚太赛，第一个学习的是这个模拟退火，但是今天想要更新的不是模拟退火，而是遗传算法；

今天学习的这个遗传算法和我们之前熟知的这个粒子群，蚁群，模拟退火之类的这个算法都是启发式的算法，也叫做智能算法，这样的方法不同与我们前期学习的这个基本的算法，可能是因为这样的方法在这个运行过程中出现的这个结果是存在误差的；就是我们每一次的这个运行的结果是不一样的；

启发式算法就是根据我们的最优化的算法提出来的，我们的这个启发式算法是基于我们的这个经验或者是操作，得到的不是这个最优解，但是我们的这个启发式算法得到的这个解与这个最优解之间的这个误差我们是可以接受的；

无论是模拟退火，还是这个今天介绍的这个遗传算法，可能他们的这个背景不一样，例如我们的这个遗传算法可能是和这个进化相关的（就是我们的优胜劣汰，留下来的这个就是我们最终确定的最优解）；我们的这个模拟退火就是根据这个传统的这个物理学的这个降温的过程进行模拟的，两个是可以进行类比的；

其实我认为这些都不是主要的，主要是这些算法的这个背景虽然不同，但是他们的这个思想内核是一样的，就是通过不断的更新和迭代，避免陷入这个传统的解法导致的这个局部最优解，而是尽可能的找到全局的最优解；

例如我们的这个模拟退火求解这个最大值的爬山法，我们想要达到这个最高点，传统的这个解法就是我们达到这个局部的最高点之后，两边这个时候都是比我们小的，这个时候我们就不会继续进行遍历搜索了，但是我们的这个模拟退火达到这个局部的最优解之后，即使两边的这个数值比这个点小，但是我们还会以一定的概率接受这个新解（这样就可以跳出这个局部的最优解，进而可能找到这个全局最优解）；

我们的这个遗传算法也是类似的，是通过这个交叉以及这个变异的方式不断的进行迭代和更新，这样做的目的也是为了跳出这个局部的最优解，找到全局的最优解，两个可谓是殊途同归，只不过这个方式不一样罢了，但是这个方式仅仅是两个算法的这个背景不一样，但是他们的这个思想内核不一样；

当然，上面的这个仅仅是我当前阶段的体会，可能一些地方不正确，但是随着这个学习的深入，相信我们都会有新的理解和体会的~~

2.生物学基础

这个遗传算法和我们的生物学是有很大的渊源的：

我们对于这个遗传算法的学习到的生物学基础，需要和我们的数学建模里面的概念进行类比，这个是学习好这个遗传算法的关键，我们的这个遗传算法里面的这个概念和我们的数学建模里面的这个术语是一一对应的；

2.1适应度

例如，我们的这个遗传算法里面的下面的这些对应的关系：（图片来自于这个大连大学的数学建模的官方账号，仅为学习交流，我认为这个里面是学生投稿，讲的还是很通俗易懂的，毕竟同为学生嘛，相同的这个身份可能让我们的之间更默契一些，我也推荐感兴趣的小伙伴去进行学习）；

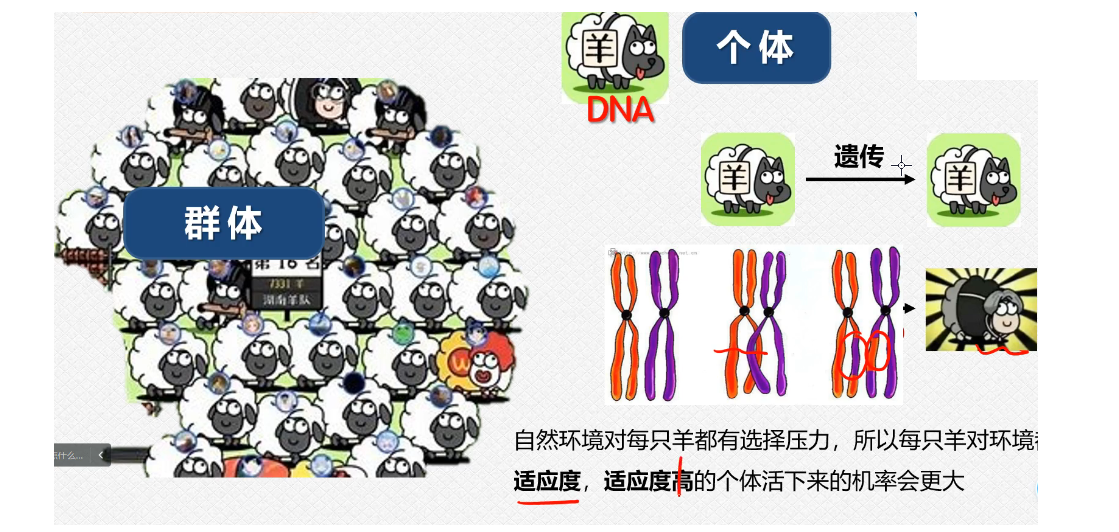
我们的这个适应度越高，这个动物进化之后生存下来这个概率就会越大，这个其实类比到我们的这个数学建模里面，就是我们的这个解越接近于这个最优值，留下来的这个概率就会越大（因为这个过程实际上是随机生成数据，然后进行判断，如果我们的这个随机数据的目标函数值差得很远肯定就会被淘汰嘛，剩下的就是比较接近这个最优解的数据，在这些数据里面不断的进行迭代，尽力去找到这个最优解，这个过程实际上就是我们的不断适应环境的过程，我们的生物会被淘汰，我们的这个不符合条件的数据也是会被淘汰掉的；

2.2染色体，基因

我们的这个生物学的概念：染色体就是我们的求解过程中的可行解；

我们的这个可行解的元素就是这个生物学里面的基因；

适应度函数其实和我们的这个目标函数之间也会存在着关联的

3.算法介绍

3.1算法流程

下面的这个流程就是我们针对于一个实际问题的分析过程，这个就是我们求解问题的一个思路；

我们在这个真实的数学建模比赛里面，也是需要画出来这样的图表示我们的这个解题思路的，我们只需要在了解这个题目的原理的基础上面，对于这个流程图里面添加这个题目对应的内容，这样我们的这个流程图就可以在我们自己的这个理解之下，放在论文里面了；

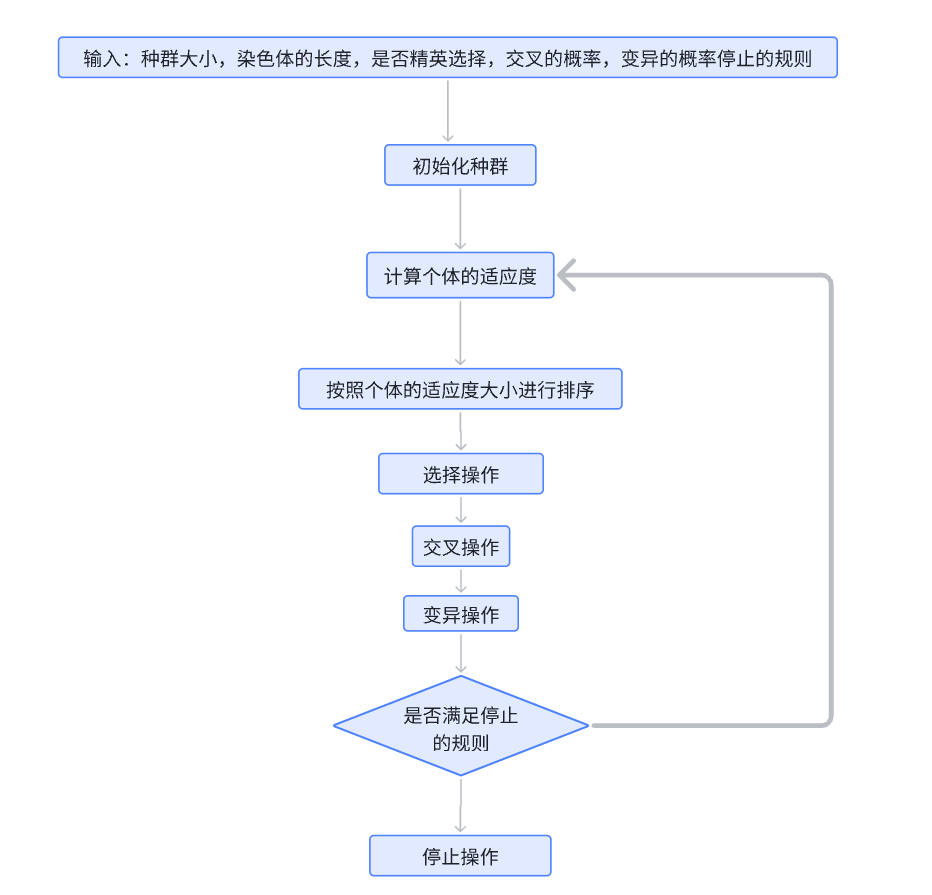
我来还原一下这个遗传算法的整个的流程：

3.2编码和解码

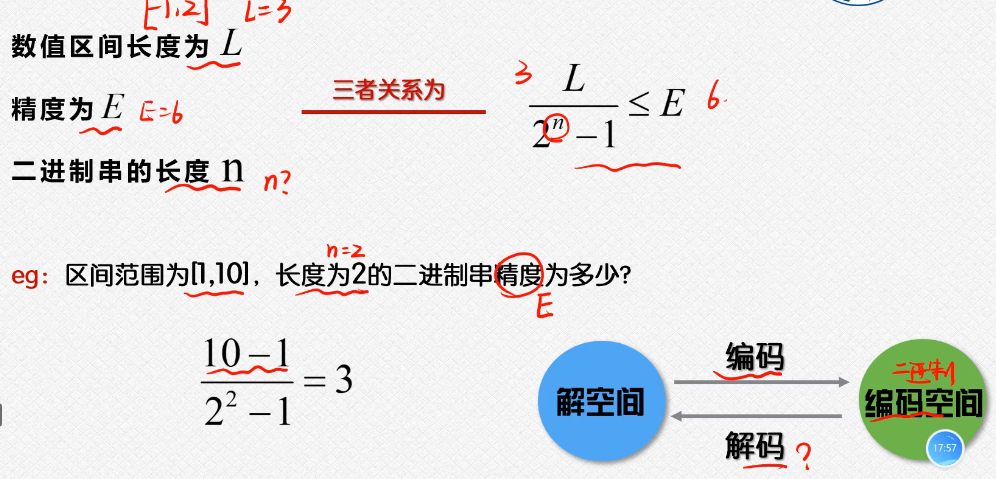
编码和解码：这个涉及到了这个二进制和我们的十进制之间的这个转换；

上面的这个里面是根据我们的这个区间的长度和我们的二进制串的长度和我们的精度之间需要满足的这个不等式的关系；

解码，就是我们的这个二进制数据转换为这个十进制的数据的过程（实际上是用的就是我们的短除法，然后把这个余数倒着写就可以了）；

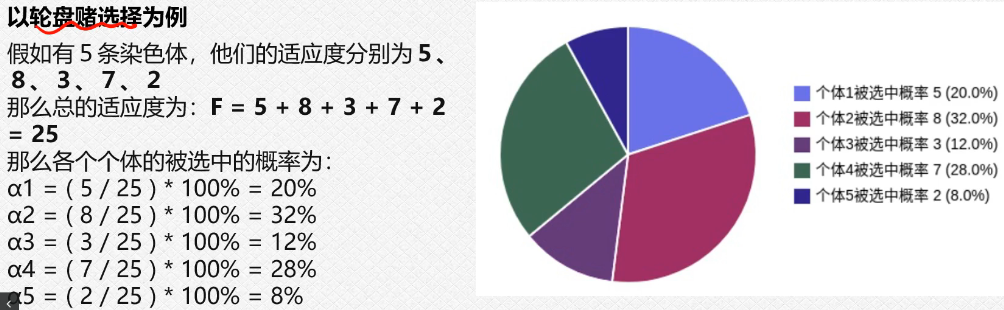
3.3轮盘赌选择

就是我们的这个出现的概率越大，我们留下来的这个概率就越大，我们后面进行迭代的时候，就会使用概率大的作为我们的初始化的对象（因为我们的这个过程需要迭代，第一次初始化是随机的，经过这个第一轮之后我们就可以选择这个概率大的进行初始化操作）；

3.4交叉和变异

这个主要是基于这个二进制的编码进行操作的：

交叉可以理解为这个生物学上面的染色体之间的这个交叉变换；

变异就是这个染色体上面的这个基因发生突变，这个就是变异；

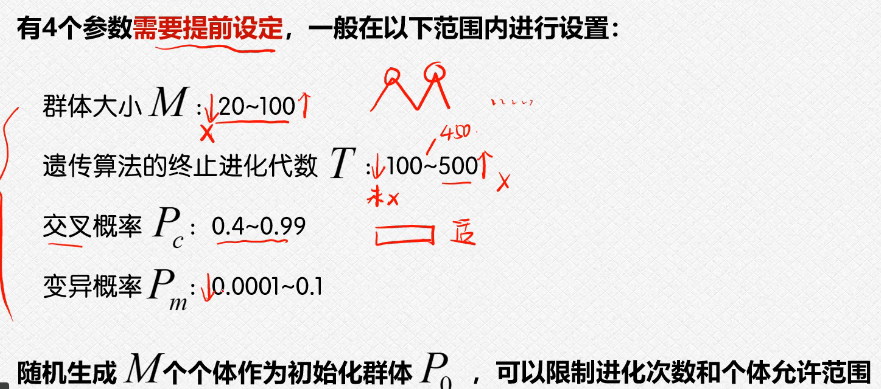
3.5初始参数的设置

1）初始化种群的大小

2）迭代的次数：这个就是100,200之类的，看情况；

3）交叉的概率：这个值是在0-1之间但是这个数值，一般是比较接近于这个1的；

4）变异的概率：这个数值也是在0-1之间，但是这个值接近于0，不会很大；

4.实际应用-matlab

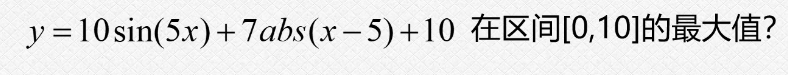
4.1观察图像

我们通过这个matlab做出来这个函数的图像，这个图像可以看到是很容易陷入到这个局部的最优解的，我们可以直观的看到这个在0-1之间的这个某一位置出现了50多的一个最大的数值；

我们的这个问题就是为了找出来这个特例，使用这个特例去验证我们的遗传算法，因为如果是一个没有这么多的局部最优解的情况，我们的普通的方法也是可以做出来的；

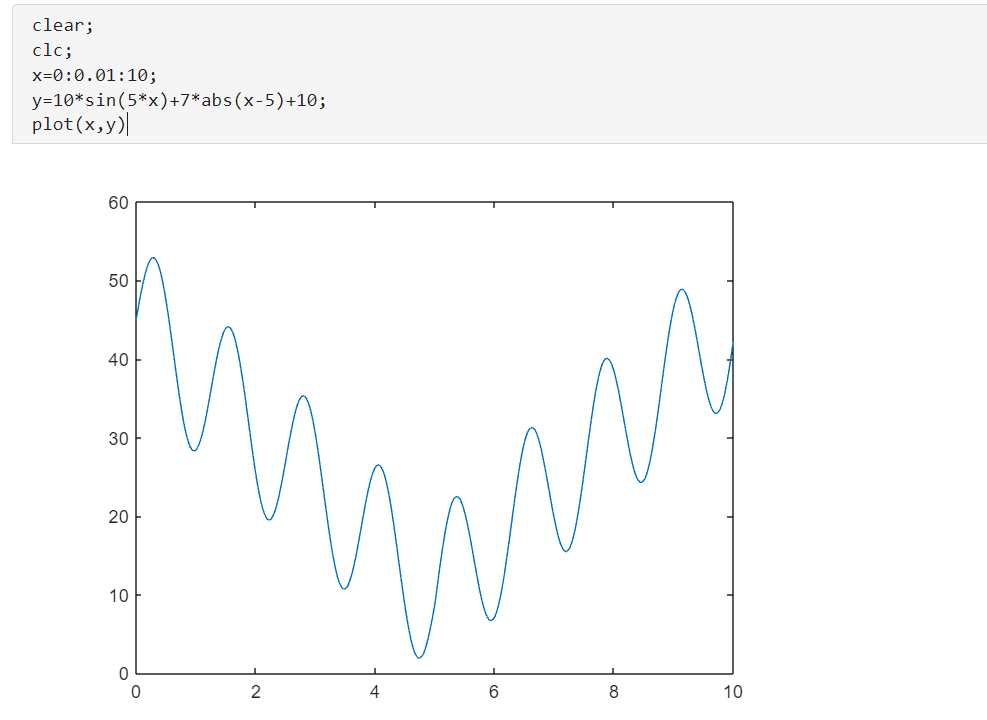
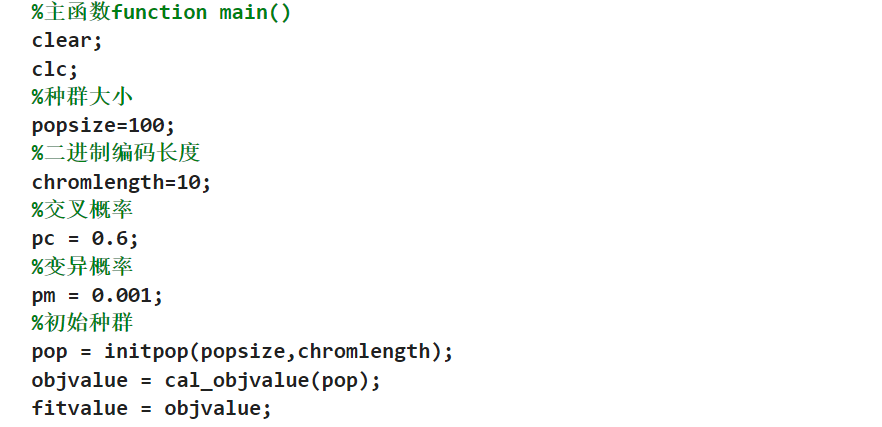
4.2初始参数说明

100表示的就是我们的群体的大小；

10表示这个二进制编码的长度是10；

这个里面的这个交叉的概率和变异的概率的这个数值的大小也是符合我们上面说的这个规则的，这个变异的概率一定是很小的；

4.3init初始化

这个里面使用的rand表示生成的数据就是在这个0-1之间的数据，外面加上这个round之后这个数据就是进行四舍五入，这其实就是把这个初始化的矩阵里面的这个数据全部是01，不是0就是1；

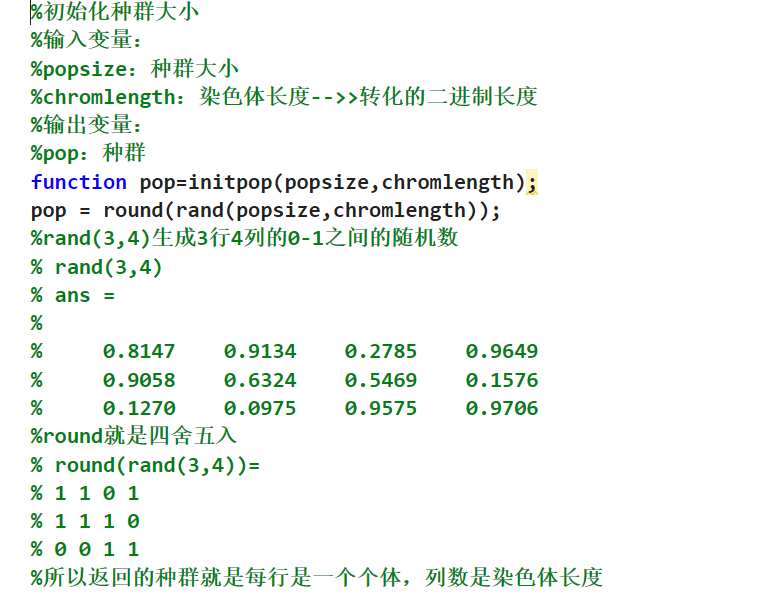
4.4二进制转换为十进制

这个循环主要是为了这个让矩阵的每一列乘以对应的这个数量级，例如这个是100*10的矩阵，第一列全部乘以10^{9，以此类推，最后一列乘以这个10}0，然后这个sun函数里面的这个第二个参数表示的是：对于每一行进行求和操作；

sum其实进行的就是这个二进制数据的计算，*10、1023这个就是我们上面说的这个关于误差E的公式，如果不懂的话强烈推荐去看这个连大数学建模官方账号里面的这个视频，真的讲的贼清楚；

4.5选择,交叉过程

cumsum函数：上面的这个其实是进行的选择过程，这个核心的思路就是我们的轮盘赌过程的这个思路，这个过程还是稍微有些复杂的；

cumsum函数情况如下：这个实际上是类似于这个前n项和的过程,把这个数据当做数列的话，第一个数据就是S1，第二个数据就是S2=a1+a2以此类推下去；

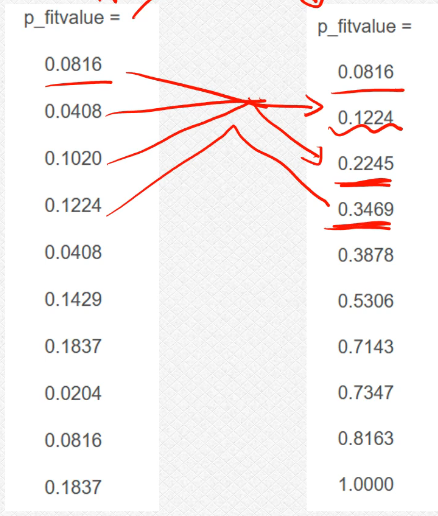
4.6情况说明

这个过程没有结束，但是我就不往下说明了，这个其实后面的这个交叉包括变异的过程还是很复杂的，我觉得这个主要还是理清这个遗传算法的整个思路，然后再这个实际题目里面去应用，这个是主要的，这个一个函数求极值的这个问题如果真的使用这个遗传算法求解就有些大材小用了，因为这个遗传算法过程繁琐，即使我们不使用这个遗传算法，我们使用其他的这个方法，可能也是可以得到不错的结果的；

我自己的这个观点就是对于这个模拟退火，遗传算法，群类算法（蚁群，粒子群）之类的，我们可以去了解（我的这个文章对于遗传算法就是了解层面，都是我对于up主讲授内容的理解），我们选择一个深入学习就可以了，因为他们的这个思想内核是一样的，我们在一次比赛里面总不能都是用吧，这样写不合适，当然，这个过程需要我们不断的学习，自己去体会这个算法在我们的数学建模赛题里面的运用；

4.7代码

这个其实在up的视频下面是有这个网盘链接的，找不到的话可以看这个：

%main方法
%主函数function main()
clear;
clc;
%种群大小
popsize=100;
%二进制编码长度
chromlength=10;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群
pop = initpop(popsize,chromlength);
objvalue = cal_objvalue(pop);
fitvalue = objvalue;for i = 1:100%选择操作newpop = selection(pop,fitvalue);%交叉操作newpop = crossover(newpop,pc);%变异操作newpop = mutation(newpop,pm);%更新种群pop = newpop;%计算适应度值（函数值）objvalue = cal_objvalue(pop);fitvalue = objvalue;%寻找最优解[bestindividual,bestfit] = best(pop,fitvalue);x2 = binary2decimal(bestindividual);x1 = binary2decimal(newpop);y1 = cal_objvalue(newpop);if mod(i,10) == 0figure;fplot('10*sin(5*x)+7*abs(x-5)+10',[0 10]);hold on;plot(x1,y1,'*');size(x1)title(['iteration times n=' num2str(i)]);%plot(x1,y1,'*');end
end
fprintf('The best X is --->>%5.2f\n',x2);
fprintf('The best Y is --->>%5.2f\n',bestfit);

%selection.m文件
%如何选择新的个体
%输入变量：pop二进制种群，fitvalue：适应度值
%输出变量：newpop选择以后的二进制种群
function [newpop] = selection(pop,fitvalue)
%构造轮盘
[px,py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
p_fitvalue = cumsum(p_fitvalue);%概率求和排序
ms = sort(rand(px,1));%从小到大排列
fitin = 1;
newin = 1;
while newin<=pxif(ms(newin))<p_fitvalue(fitin)newpop(newin,:)=pop(fitin,:);newin = newin+1;elsefitin=fitin+1;end
end

%变异的过程：
%关于变异
%函数说明
%输入变量：pop：二进制种群，pm：变异概率
%输出变量：newpop变异以后的种群
function [newpop] = mutation(pop,pm)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:pxif(rand<pm)mpoint = round(rand*py);if mpoint <= 0;mpoint = 1;endnewpop(i,:) = pop(i,:);if newpop(i,mpoint) == 0newpop(i,mpoint) = 1;elseif newpop(i,mpoint) == 1newpop(i,mpoint) = 0;endelse newpop(i,:) = pop(i,:);end
end

%初始化种群大小
%输入变量：
%popsize：种群大小
%chromlength：染色体长度-->>转化的二进制长度
%输出变量：
%pop：种群
function pop=initpop(popsize,chromlength);
pop = round(rand(popsize,chromlength));
%rand(3,4)生成3行4列的0-1之间的随机数
% rand(3,4)
% ans =
% 
%     0.8147    0.9134    0.2785    0.9649
%     0.9058    0.6324    0.5469    0.1576
%     0.1270    0.0975    0.9575    0.9706
%round就是四舍五入
% round(rand(3,4))=
% 1 1 0 1
% 1 1 1 0
% 0 0 1 1
%所以返回的种群就是每行是一个个体，列数是染色体长度

%交叉变换
%输入变量：pop：二进制的父代种群数，pc：交叉的概率
%输出变量：newpop：交叉后的种群数
function [newpop] = crossover(pop,pc)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1if(rand<pc)cpoint = round(rand*py);%交叉点计算newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];elsenewpop(i,:) = pop(i,:);newpop(i+1,:) = pop(i+1,:);end
end

%计算函数目标值
%输入变量：二进制数值
%输出变量：目标函数值
function [objvalue] = cal_objvalue(pop)
x = binary2decimal(pop);
%转化二进制数pop为x变量的变化域范围的数值
objvalue=10*sin(5*x)+7*abs(x-5)+10;

%二进制转化成十进制函数
%输入变量：
%二进制种群
%输出变量
%十进制数值
function pop2 = binary2decimal(pop)
[px,py]=size(pop);
for i = 1:pypop1(:,i) = 2.^(py-i).*pop(:,i);
end
%sum(.,2)对行求和，得到列向量
temp = sum(pop1,2);
pop2 = temp*10/1023;

%求最优适应度函数
%输入变量：pop:种群，fitvalue:种群适应度
%输出变量：bestindividual:最佳个体，bestfit:最佳适应度值
function [bestindividual bestfit] = best(pop,fitvalue)
[px,py] = size(pop);
bestindividual = pop(1,:);
bestfit = fitvalue(1);
for i = 2:pxif fitvalue(i)>bestfitbestindividual = pop(i,:);bestfit = fitvalue(i);end
end