精华帖分享|缠论系列 -笔
本文来源于量化小论坛策略分享会板块精华帖,作者为吴奕萱,发布于2023年6月4日。
以下为精华帖正文:
01
笔
昨天讲了3根K线组合关系的完全分类,按照逻辑,其实我们会考虑是不是应该讲4根、5根K线的组合关系了。
精华帖分享 | 缠论系列
的确如此,在讲缠师的笔之前,我们来聊聊,为什么从3根K线之后,就是笔的出现,而不是更多根K线组合?
先来看看4根K线的组合关系完全分类,很容易得出,从高低点比较的情况的来看,是有4*2 = 8种情况的。
我们来比较下:
3根K线的情况下,转折最高点和最低点的位置出现在哪里是有迹可循的:
顶分型的最高点,肯定在第2根K线;
底分型的最低点,肯定在第2根K线;
4根K线的情况下,画图举个例子吧:
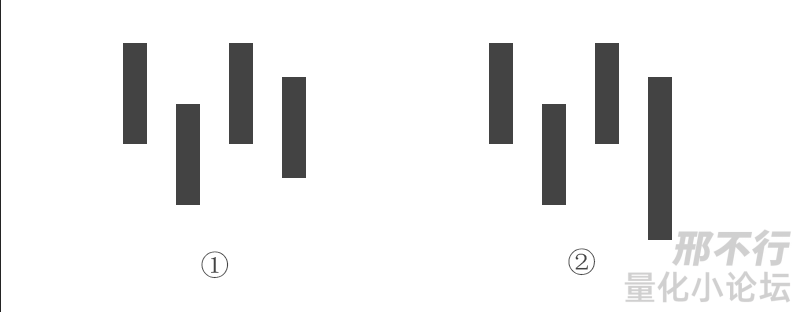
最低点在哪?可能在第二根,可能在第4根。
那么5根K线,6根K线,可能会更加犬牙交错,情况会更加复杂。
所以缠师忽略了这一些波动,工具用的就是笔!(这里的信息也会缺失)
当然笔的出现,原因肯定不在与此,这个后面聊到动力学的时候,还可以再分析一遍,聊到两者结合的时候还可以再分析一遍,我们这里仅仅从形态学处理的角度出发,讲了我的一点片面的观点。前面我尽量不讲没出现过的概念和解释。
到这里为止,我们来想想我们是怎么从分笔数据到笔的概念的,分笔数据 → 和成K线 → K线包含 → K线分型 → 笔,再这些最小的概念里面,我们还忽略了一个东西:缺口!
为什么之前没有讲缺口这个概念,是因为缺口,代表的东西有些复杂。
(缺口在不同的情况下,在形态学上都有不同的用法,但背后的原理又是动力学的东西,形式上要涉及到中枢,级别,所以在没有讲走势级别和动力学前,挺不好说的。)
这里简单一点,大部分的缺口,可以看成独立的1根虚拟K线,后面我们再详细说,缺口成K,缺口成笔,甚至成段的条件。(这一部分,成段是原文有出处的,成笔和成K是推理出来的)
下一篇,我们讲笔的定义。
02
笔的定义
网络上的笔概念杂七杂八的特别多,但原文中,只有两种,一种是老笔(严格笔),一种是新笔(宽松笔)。
老笔和旧笔定义的规则都是动力学原理,后面讲动力学的时候可以讨论一下。
在讲笔定义之前,还需要了解2个小学数学上的定义:结合律和交换律(牢记,后面时刻都要用!)
举个简单的例子:
结合律:a + b + c = (a + b) + c = a + (b + c) ;只要算子的位置没变,其运算顺序就不影响运算结果。
交换律:a + b = b + a ; 算子的位置改变,不影响运算结果。
K线本身具有时间序列的属性,两根K线是否能交换位置,还能保持原来的信息含量,显然是不能的。那么笔的定义也只符合结合律,而不符合交换律的。(牢记牢记)
严格笔的定义:
所谓笔,就是顶和底之间的其他波动,都可以忽略不算(65原文)。
两个相邻的顶和底之间构成一笔(65原文)。
注意:一定是相邻的顶和底,隔了几个就不是了(65原文)。
必须遵守结合律(原文)。
上升笔:底分型+上升K线+顶分型(65原文)
下降笔:顶分型+下降K线+底分型(65原文)
其实这个不太合适用上升K线和下降K线的说法,更合适的是独立K线(这两种K线都是一种组合关系,缠师实际是用独立K线,后文也有提到77课)。
上升笔(改):底分型+N根独立K线+顶分型,N>0
下降笔(改):顶分型+N根独立K线+底分型,N>0
在同一笔中,顶分型中最高那 K 线的区间至少要有一部分高于底分型中最低那 K 线的区间(77原文)。
如图(以上升笔为例)
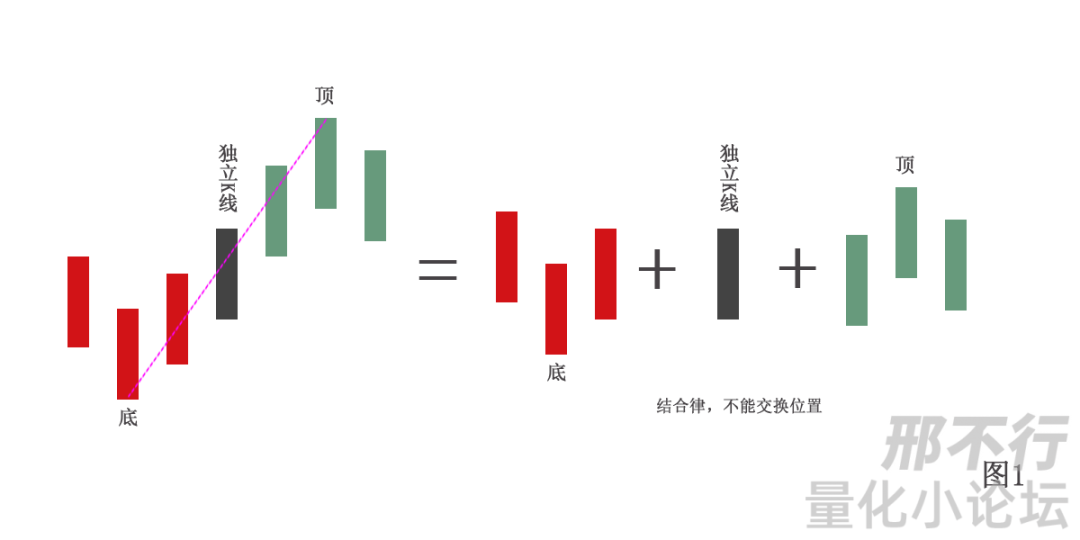
新笔定义:
顶分型和底分型经过包含关系处理后,不允许公用K线(81原文)。
顶分型的最高原始K线和底分型的最低原始K线间(不包含这两根),至少有3根K线(不考虑包含关系),即大于等于3根原始K线。(81原文)。
以底分型最小模型为例(顶分型的最小模型可以自行去画一下),如图:
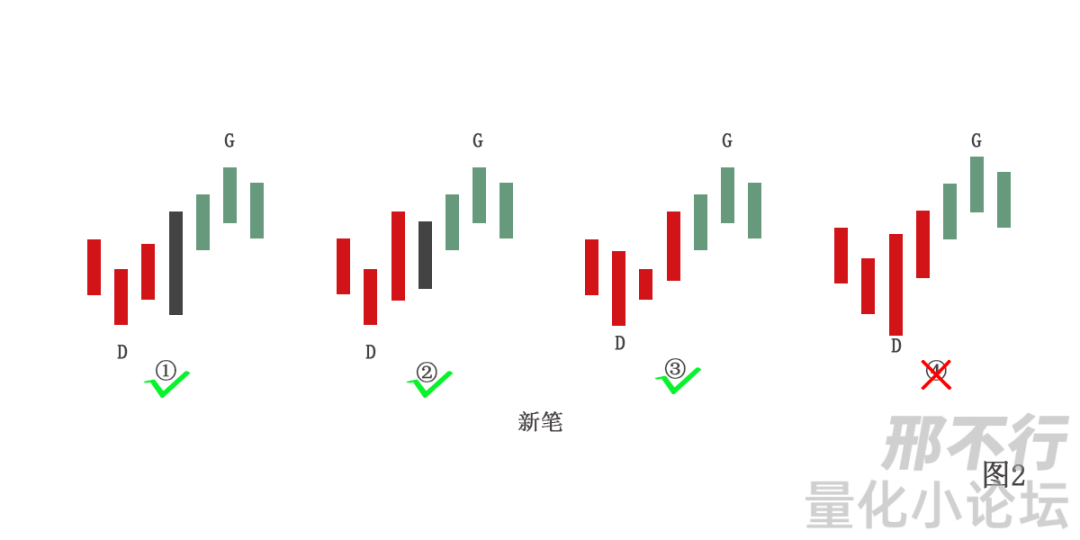
这里按照定义,1号2号3号是满足条件的,而4号是不满足条件的,原因是D和G之间不满足3根K条件。
按照完全分类的思想,这里还需要考虑一种情况,就是缺口,因为从笔开始,就要考虑到缺口因素了,那么有缺口的情况怎么算?
如图:
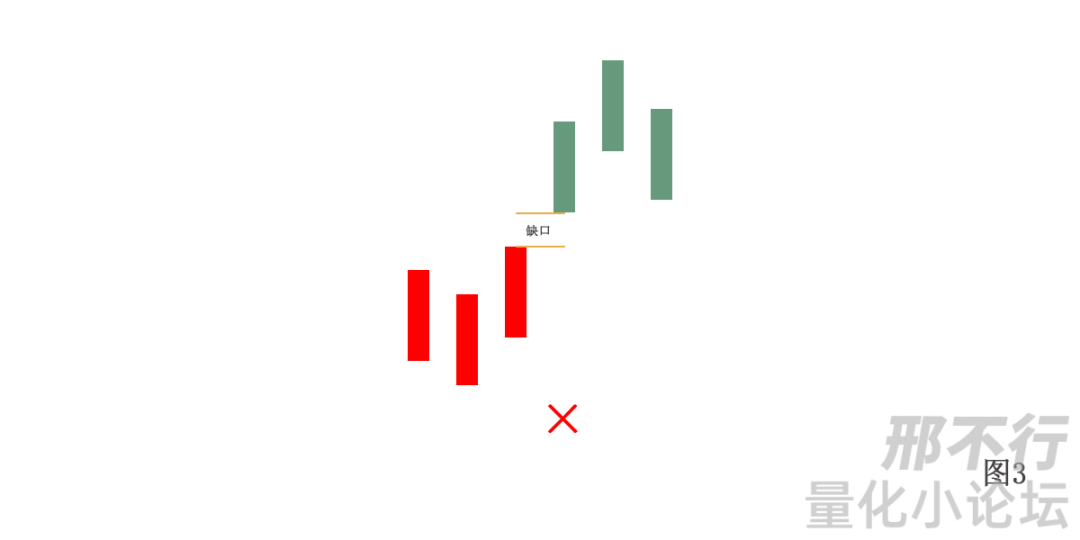
缠师是有在回复里面说过这个问题的,当时他讲的是不可以成立,原因是时间因素特别重要!(81回复)
但是原文中,缺口又有成段的论述,所以这里的不成立,只是一般状态。具体的成段成笔的条件,需要等到讲中枢,讲走势的时候再进行讨论。
所以,在不满足时间因素的时候,也就是K线根数的条件下,缺口一般是没有形态学意义的。如果满足了K线根数的条件下,一般情况,缺口在形态学中只是代表了一根普通的K线,只有在极为特殊的时候,缺口能成笔,成段。
那么新笔,老笔,用什么?
缠师的回复是,他一直用的都是老标准。
新笔和老笔的差别在哪里,从信息学角度,和实用主义的角度,或者别的角度,大家可以讨论下。
下一章,讲讲画笔的步骤。
03
笔的步骤
前文有一点忘记展开来详细说说了,就是“从分型到笔,必须是一顶一底”。
那么,两个顶或者底能不能构成一笔?
完全分类有两种情况:
在两个顶或底中间,有其他的顶和底;
在两个顶或底中间,没有其他的顶和底。
我尝试用图来表达下:
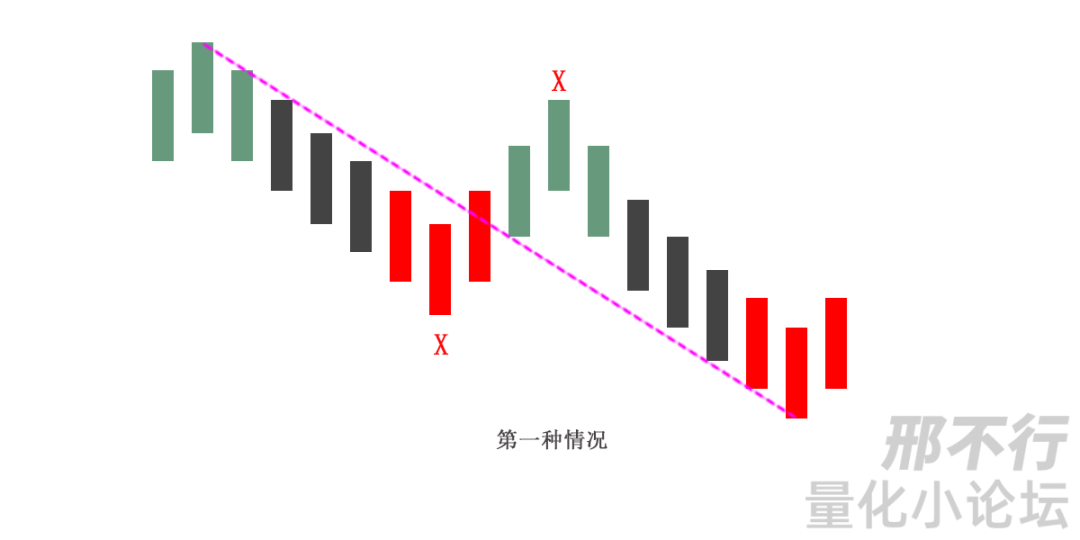
第一种情况,在两个顶或底中间有其他的顶和底,这种情况,只是把好几笔当成了一笔,所以只要继续用一顶一底的原则,自然可以解决;如上图中的两个绿色的顶分型,中间有一个底分型。
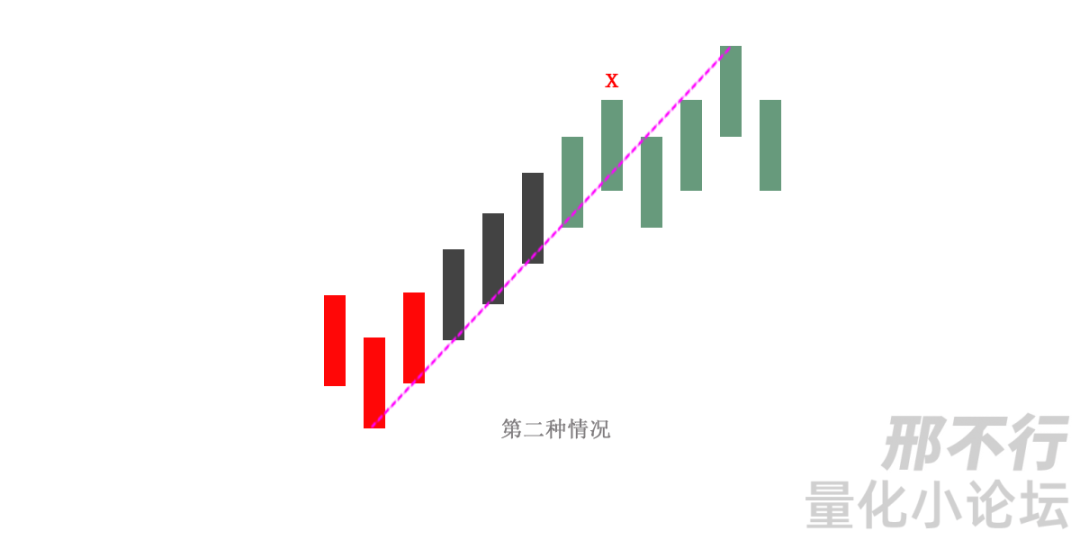
笔的定义清楚了之后,我们来聊聊该画笔的流程,这个对我们量化思路的整理很有效果。
缠师在原文中讲过一套画笔的方法,我这里先复现一下,然后再聊聊我的思路。
缠师画笔方法:
确定所有符合标准的分型。
相邻无共用K线;
如果前后两分型是同一性质的:
对于顶,前面的低于后面的,只保留后面的,前面那个可以 X 掉;
对于底,前面的高于后面的,只保留后面的,前面那个可以 X 掉;
不满足上面情况的,例如相等的,都可以先保留。
经过步骤2的处理后,余下的分型,如果相邻的是顶和底,那么这就可以划为一笔。如果相邻的性质一样,那么必然有前顶不低于后顶,前底不高于后底:
在连续的顶后,必须会出现新的底,把这连续的顶中最先一个,和这新出现的底连在一起,就是新的一笔,而中间的那些顶,都 X 掉;
在连续的底后,必须会出现新的顶,把这连续的底中最先一个,和这新出现的顶连在一起,就是新的一笔,而中间的那些底,都 X 掉。
如图:
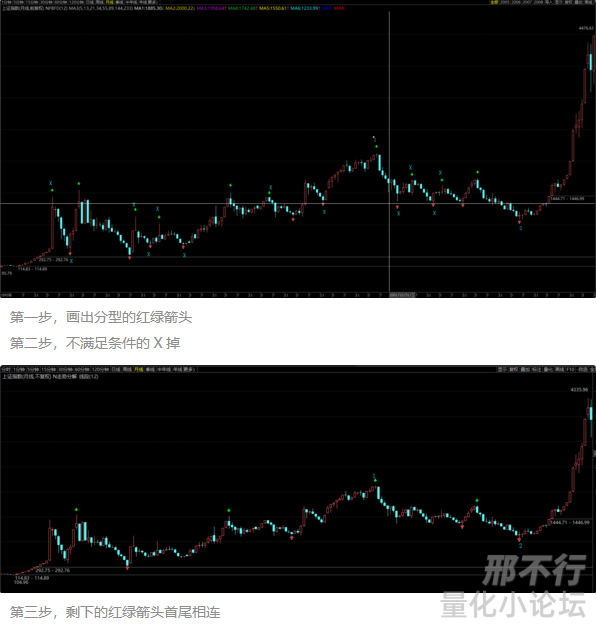
(大家仔细看,这个图里面有没有不符合操作的规则的顶底分型)
是不是,感觉很简单,但是实际操作下来,这里面有个小情况,然后缠师也有前后矛盾的地方。
先看图:
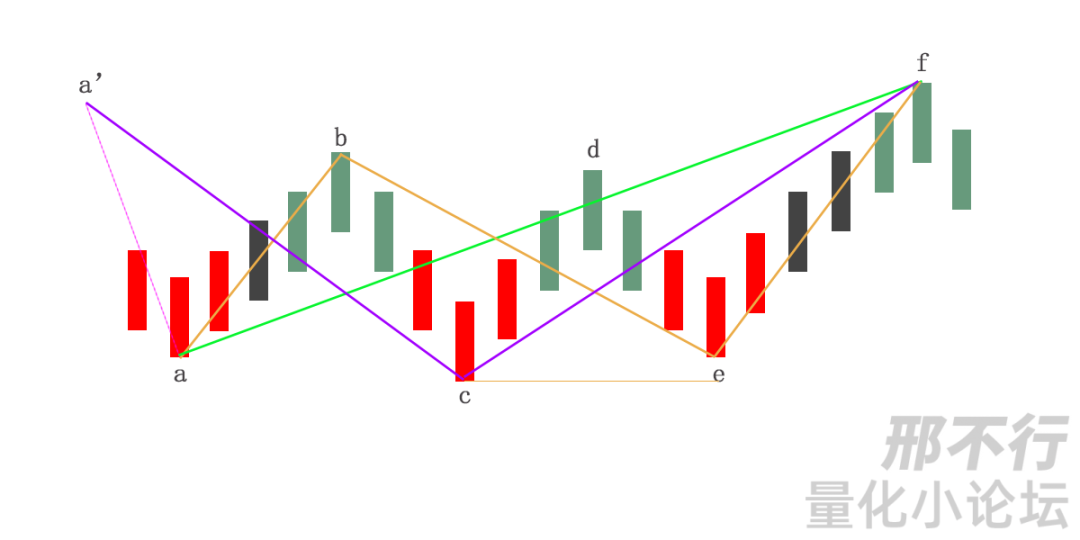
这张图,从a'到f这个笔该怎么来划分?
按照缠师的步骤,c、e这2个分型都是不符合标准的,这样说起来,应该是a'a,af这样的划分,如同图中的绿色笔。
那么问题来了,a点是比c点高的,而缠师有在61课的回复中有讲过,我贴下原文:
Q:一笔是否也有类似线段那样得三角形态或奔走形态?或者说,一笔之中的非顶、底 K 线是否允许超出顶底的范围呢?顶或底是否一定为一笔的最高点或最低点呢?
缠中说禅:一笔,是一顶一底,怎么会有三角形?顶和底,当然一定是那一笔的最高最低,如果不是,那里面一定不只一笔。
这句话:【当然一定是那一笔的最高最低】,但是图中c点是比a要低的。
ok,有问题!
后面,缠师又在77课的中有个回复,我引述一下:
Q:请问下图中的笔,是AD一笔呢?还是AB,BC,CD三笔呢?
缠中说禅:AB肯定不是一笔,BC也不是,至于AD是不是,这要看D后面的走势。
找笔,首先要找分型。A、D都满足分型的条件,但关键看D后面的分型是顶还是底,如果是顶,那么AD就是一笔。如果是底,那D肯定不是和A构成一笔的那个底。
附图:
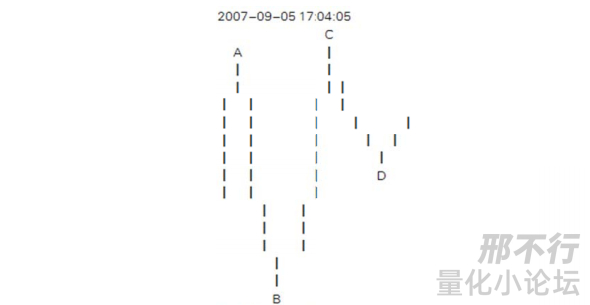
如果AD成一笔,那么这一笔的最低点在B,而不在D,和61课中的回复是矛盾的。
【注:当然这个图是有问题的,C比A高,所以连到A的这一笔,到C应该是延续,所以个人觉得,这个笔应该是到C一个上升笔,CD一个下降笔。】
【这里感谢下顾同学,因为以前CD这里我是不算笔的。】
如果按照71课的回复,那么我们上图的a'到f的划分,可以是按照黄色线的划分也是可以的。
还有个紫色的,大家看完,可以自行分析。
我们再来看看缠中说禅笔定理:
缠中说禅笔定理:任何的当下,在任何时间周期的 K 线图中,走势必然落在一确定的具有明确方向的笔当中(向上笔或向下笔),而在笔当中的位置,必然只有两种情况:
在分型构造中;
分型构造确认后延伸为笔的过程中。
根据这个定理,对于任何的当下走势,在任何一个时间周期里,我们都可以用两个变量构成的数组精确地定义当下的走势。
第一个变量,只有两个取值,1 代表向上的笔,-1 代表向下的笔;
第二个变量,只有两个取值,0 代表分型构造中,1 代表分型确认延伸为笔的过程中。
那么这两个变量,在完全分类下,只有4种情况:
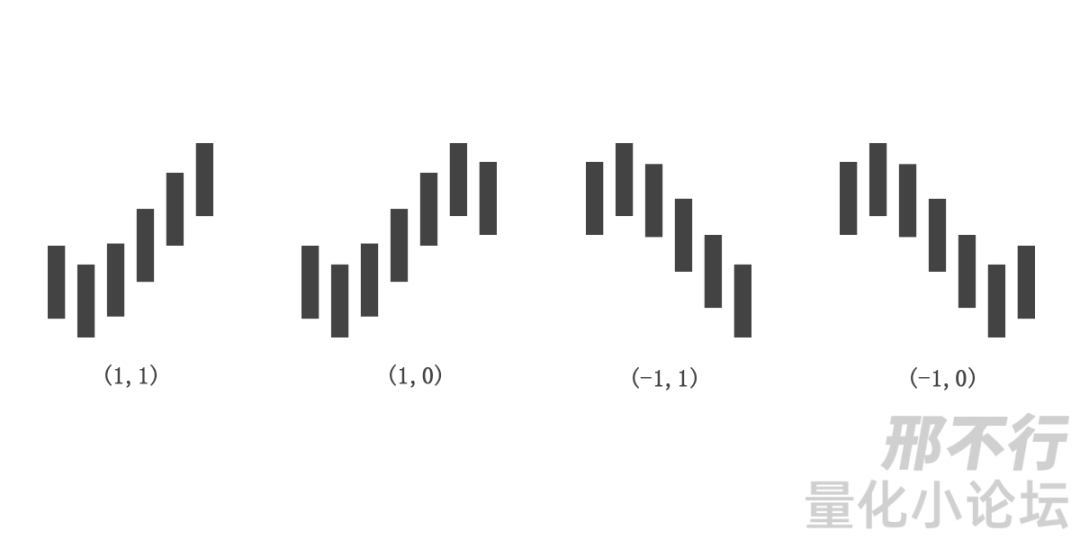
(1,1) :代表着一个向上的笔在延伸之中;
(1,0) :代表向上的笔出现了顶分型结构的构造;
(-1,1):代表向下的笔在延伸中;
(-1,0):代表向下的笔出现底分型的构造。
如下图:
这里要注意的是分型构造和分型确认的区分:
分型构造:出现顶底分型后,一直到满足笔的最低数量K线(5根K线)出现前的状态都是分型构造的状态。
分型确认,是指分型构造完成后,在满足笔的最低数量K线之后,该分型就确认了。
如下图:
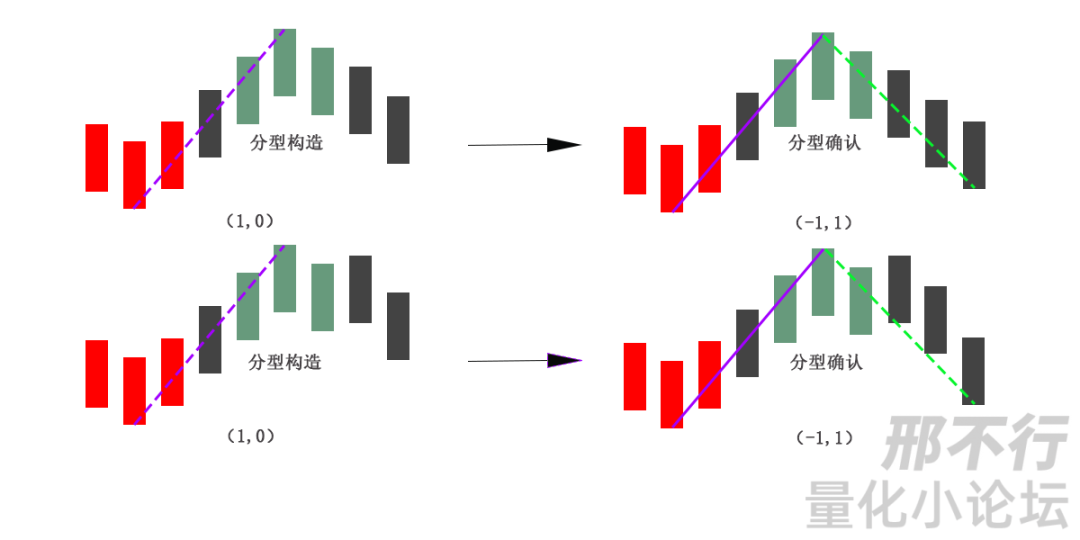
上图中:
1、所有的红色的底分型,都是已确认的状态,而左边的绿色的顶分型,都是在构造状态,右边的绿色顶分型就是确认的状态!
2、虚线表示延伸中的笔(因为分型构造没有完成),而实线表示完成的笔(分型已经确认,反向笔正在延伸)。
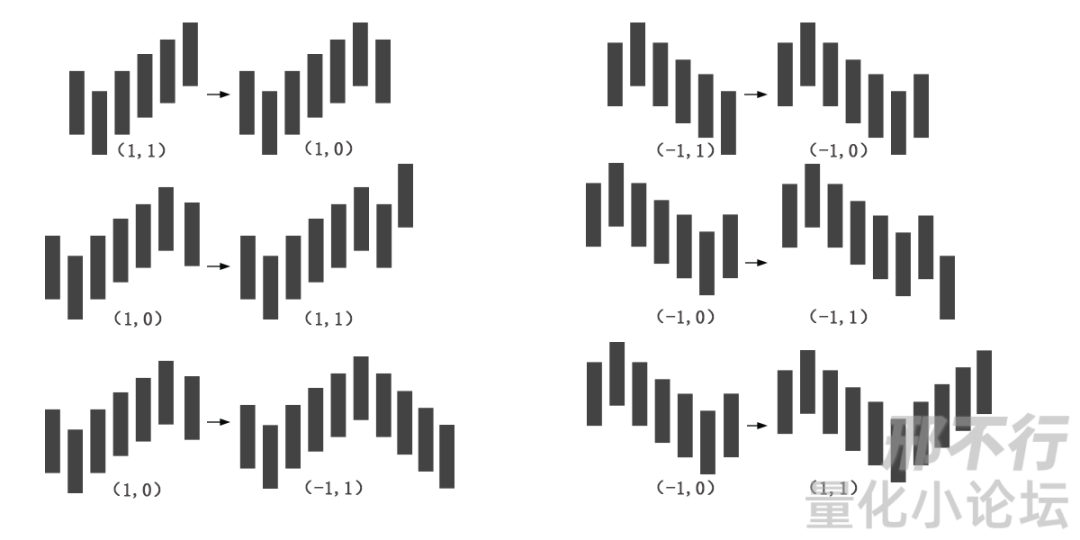
这四种状态也不是随便两两连接的,总共分为6种情况(完全分类):
(1,1) 连接 (1,0);
(-1,1) 连接 (-1,0);
(1,0) 连接 (1,1) ;
(1,0) 连接 (-1,1);
(-1,0) 连接 (-1,1);
(-1,0) 连接 (1,1) ;
如下图:
分型一旦确定,不可修改(这句话有原文);
笔的确定可以通过分型的构造和确认形成,这种方法是可以再当下去确认笔的状态的。
根据上述笔定理,讲讲我的画笔的流程: