当前位置：首页 > news >正文

LeetCode 0685.冗余连接 II：并查集（和I有何不同分析）——详细题解(附图)

news 2024/11/5 13:30:58

【LetMeFly】685.冗余连接 II：并查集（和I有何不同分析）——详细题解(附图)

力扣题目链接：https://leetcode.cn/problems/redundant-connection-ii/

在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。每个元素是一对 [u_i, v_i]，用以表示有向图中连接顶点 u_i 和顶点 v_i 的边，其中 u_i 是 v_i 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

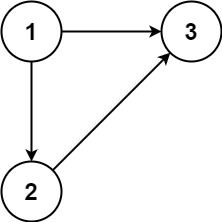
输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

示例 2：

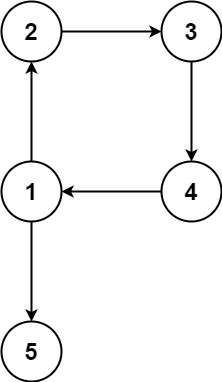
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

提示：

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= u_i, v_i <= n

解题方法：并查集

并查集

解题思路

这题和684.冗余连接的区别是：

684的无向图只需要考虑有没有形成自环，而本题有向图还需要考虑“是否形成了入度为2的节点”。

如果形成了“入度为2”的节点，例如下面两种情况，在684.冗余连接中只需要移除“首次形成(无向)环”的边，而在685.冗余连接II中就不能只移除“最后出现的导致形成(无向)环的边”：

1----->2      1------+
↑      ↑      ↑      ↓
3------+      2<-----3<---4
左图中只能移除[1,2]或[3,2]而不能移除[3,1]；右图中只能移除[1,3]而不能移除[3,2]或[2,1]。

有向边不能和无向边一概而论的本质原因是：树中一个节点不能有两个父节点，即入度不能为2。所以，一旦出现了入度为2的节点 $n o d e$ ，就要在“终点为 $n o d e$ 的两条边”里面选择一条移除。判断方法如下：

尝试移除一条边，判断剩下的边（不考虑方向）能否构成无向环，如果不构成无向环则说明这条边可以被移除。

判断方法就和684题一模一样了，使用并查集即可完成判断。

树上多一条边就一定存在入度为2的节点吗？不一定，还可能有以下这种情况：

1------+
↑      ↓
2<-----3----->4
图中节点[1,2,3]形成了一个环，但1、2、3、44个节点的入度都为1。

这样就和684题一模一样了其实，在环[1,2,3]里任意移除一条边图都能变成树。

同样使用并查集，返回第一条“形成环”的边即为所求。

解题方法

首先统计是否有入度为2的节点：

若有，则尝试移除指向2的边（若移除后图中无环则这条边可以被移除）
否则，移除第一条导致“环出现”的边

常见问题回答Q&A

Q1： 若有入度为2的节点，在判断“移除一条边后图是否为树”时，能否通过“统计每个点是否孤立(入度出度都为0)”来判断？

例如下图中终点为3的边有[1,3]和[4,3]两条，移除[4,3]的话会导致点4成为孤立点，因此只能移除[1,3]。

1------+
↑      ↓
2<-----3<---4

A1： 不能这么判断。例如下图只能移除[2,4]不能移除[5,2]，但其实移除其中的任意一条都不会产生“孤立点”。

+---+
↓   ↑
4-->2↑
1-->5-->3

建议修改为“通过判断图是否联通”的方式判断某条边是否可以移除。

时空复杂度

时间复杂度最坏 $O(n\log n)$ ，平均为 $O(n\alpha(n))$ （接近 $O (n)$ ）
空间复杂度 $O (n)$

AC代码

C++

class Solution {
private:vector<int> fa;bool couldRemoveThisEdge(vector<vector<int>>& edges, int index) {initFa(edges.size());for (int i = 0; i < edges.size(); i++) {if (i == index) {continue;}if (find(edges[i][0]) == find(edges[i][1])) {return false;}union_(edges[i][0], edges[i][1]);}return true;}vector<int> solution_indegree(vector<vector<int>>& edges, int node) {for (int i = edges.size() - 1; i >= 0; i--) {if (edges[i][1] == node && couldRemoveThisEdge(edges, i)) {return edges[i];}}return {};  // FAKE RETURN}int find(int x) {if (x != fa[x]) {fa[x] = find(fa[x]);}return fa[x];}void union_(int x, int y) {fa[find(x)] = find(y);}void initFa(int n) {fa.resize(n + 1);for (int i = 1; i <= n; i++) {fa[i] = i;}}vector<int> solution_unionFind(vector<vector<int>>& edges) {initFa(edges.size());for (vector<int>& edge : edges) {if (find(edge[0]) == find(edge[1])) {return edge;} else {union_(edge[0], edge[1]);}}return {};  // FAKE RETURN}
public:vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {vector<bool> inDegree(edges.size() + 1);for (vector<int>& edge : edges) {if (inDegree[edge[1]]) {  // 找到了入度为2的点return solution_indegree(edges, edge[1]);} else {inDegree[edge[1]] = true;}}return solution_unionFind(edges);}
};

Python

from typing import Listclass Solution:def initFa(self) -> None:for i in range(1, len(self.edges) + 1):self.fa[i] = idef find(self, x: int) -> int:if self.fa[x] != x:self.fa[x] = self.find(self.fa[x])return self.fa[x]def union(self, x: int, y: int) -> None:self.fa[self.find(x)] = self.find(y)def couldRemoveThisEdge(self, index: int) -> bool:self.initFa()for i in range(len(self.edges)):if i == index:continueif self.find(self.edges[i][0]) == self.find(self.edges[i][1]):return Falseelse:self.union(self.edges[i][0], self.edges[i][1])return Truedef solution_indegree(self, node: int) -> List[int]:for i in range(len(self.edges) - 1, -1, -1):if self.edges[i][1] == node and self.couldRemoveThisEdge(i):return self.edges[i]return []  # FAKE RETURNdef solution_unionFind(self) -> List[int]:self.initFa()for x, y in self.edges:if self.find(x) == self.find(y):return [x, y]else:self.union(x, y)return []  # FAKE RETURNdef findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:self.fa = [0] * (len(edges) + 1)self.edges = edgeshasIndegree = [False] * (len(edges) + 1)for x, y in edges:if hasIndegree[y]:return self.solution_indegree(y)else:hasIndegree[y] = Truereturn self.solution_unionFind()

Java

class UnionFind {private int[] fa;public UnionFind(int n) {fa = new int[n + 1];for (int i = 1; i <= n; i++) {fa[i] = i;}}private int find(int x) {if (fa[x] != x) {fa[x] = find(fa[x]);}return fa[x];}public boolean isUnion(int x, int y) {return find(x) == find(y);}public void union(int x, int y) {fa[find(x)] = find(y);}
}class Solution {private boolean canRemoveThisEdge(int[][] edges, int index) {UnionFind unionFind = new UnionFind(edges.length);for (int i = 0; i < edges.length; i++) {if (i == index) {continue;}if (unionFind.isUnion(edges[i][0], edges[i][1])) {return false;} else {unionFind.union(edges[i][0], edges[i][1]);}}return true;}private int[] solution_indegree(int[][] edges, int node) {for (int i = edges.length - 1; i >= 0; i--) {if (edges[i][1] == node && canRemoveThisEdge(edges, i)) {return edges[i];}}return new int[0];  // FAKE RETURN}private int[] solution_unionFind(int[][] edges) {UnionFind unionFind = new UnionFind(edges.length);for (int[] edge : edges) {if (unionFind.isUnion(edge[0], edge[1])) {return edge;} else {unionFind.union(edge[0], edge[1]);}}return new int[0];  // FAKE RETURN}public int[] findRedundantDirectedConnection(int[][] edges) {boolean[] hasIndegree = new boolean[edges.length + 1];for (int[] edge : edges) {if (hasIndegree[edge[1]]) {return solution_indegree(edges, edge[1]);} else {hasIndegree[edge[1]] = true;}}return solution_unionFind(edges);}
}

Go

package maintype UnionFind struct {fa []int
}func New(n int) UnionFind {fa := make([]int, n + 1)for th, _ := range fa {fa[th] = th}return UnionFind{fa}
}func (unionFind UnionFind) _find(x int) int {if unionFind.fa[x] != x {unionFind.fa[x] = unionFind._find(unionFind.fa[x])}return unionFind.fa[x]
}func (unionFind UnionFind) isUnion(x, y int) bool {return unionFind._find(x) == unionFind._find(y)
}func (unionFind UnionFind) union(x, y int) {unionFind.fa[unionFind._find(x)] = unionFind._find(y)
}func canRemoveThisEdge(edges [][]int, index int) bool {unionFind := New(len(edges))for i := 0; i < len(edges); i++ {if i == index {continue}if unionFind.isUnion(edges[i][0], edges[i][1]) {return false} else {unionFind.union(edges[i][0], edges[i][1])}}return true
}func solution_indegree(edges [][]int, node int) []int {for i := len(edges) - 1; i >= 0; i-- {if edges[i][1] == node && canRemoveThisEdge(edges, i) {return edges[i]}}return make([]int, 0)  // FAKE RETURN
}func solution_unionFind(edges [][]int) []int {unionFind := New(len(edges))for _, edge := range edges {if unionFind.isUnion(edge[0], edge[1]) {return edge} else {unionFind.union(edge[0], edge[1])}}return make([]int, 0)  // FAKE RETURN
}func findRedundantDirectedConnection(edges [][]int) []int {hasIndegree := make([]bool, len(edges) + 1)for _, edge := range edges {if hasIndegree[edge[1]] {return solution_indegree(edges, edge[1])} else {hasIndegree[edge[1]] = true}}return solution_unionFind(edges)
}