聚类算法综述

摘要

聚类算法旨在根据数据中的固有模式和相似性将数据组织成组或簇。它们在当今生活中扮演着重要角色，例如在市场营销和电子商务、医疗保健、数据组织和分析以及社交媒体中。现有众多聚类算法，并且不断有新的算法被引入。每个算法都有其自身的优点和缺点，截至目前，还没有适用于所有任务的通用算法。在这项工作中，我们分析了现有的聚类算法，并从五个不同维度对主流算法进行分类：基本原理和特征、数据点分配到簇、数据集容量、预定义簇数量和应用领域。这种分类有助于研究人员从不同角度理解聚类算法，并帮助他们识别适合解决特定任务的算法。最后，我们讨论了聚类算法的当前趋势和未来可能的发展方向。我们还识别并讨论了该领域中的开放挑战和未解决的问题。

1 引言

随着数字技术的快速转型，获取信息已成为日常生活中更为普遍的方面。企业和个人现在可以访问大量信息，包括互联网上的数十亿文档、视频和音频文件。大多数企业在一个互联的数据网络中运作，这些数据链接到多个信息源，能够提供大量数据点。然而，尽管我们的计算能力在迅速增长，但数据的庞大体量常常挑战我们将分散的数据转化为有用信息、实用知识和可操作见解的能力。一种成熟的解决方案是利用机器学习，特别是聚类方法。聚类算法是机器学习算法，旨在根据特定标准将相似的数据点分组，从而揭示数据集中的自然结构或模式。其主要目的是将数据分成子组或簇，其中同一组内的项比其他组的项更为相似。聚类方法有助于信息检索、推荐系统和主题发现等多个领域的进步。

聚类算法在日常生活中无处不在。它们用于垃圾邮件分类、推荐系统、针对性营销的客户细分、基于视觉相似性组织图像的图像处理等。聚类算法不仅可以聚类基于文本的数据，还适用于音频、视频和图像。音频聚类算法使用声学特征对文件进行分组，可用于如流派识别等任务。聚类视频数据通过按视觉或主题相似性组织内容，促进推荐和摘要等任务。在图像分析中，聚类对于分割和基于内容的检索任务至关重要。聚类算法还作为检测异常的方法，无论是在网络流量、金融交易还是医疗记录中。它们的多功能性突显了其在从各种数据中提取模式和见解方面的重要性。

根据学习过程的性质和标记数据的可用性，聚类算法主要分为两类：

• 半监督学习：此类别为每个数据样本提供一个带有已知簇标签的训练数据集。算法观察训练数据集中的模式，然后学习将新数据点分配到簇中。例如受限K均值（Constrained K-Means）[1]，半监督模糊C均值（Semi-Supervised Fuzzy C-Means, SSFCM）[2]。
• 无监督学习：在此类别中，不提供标记数据集。算法识别数据中的模式和结构，然后基于特征中的内在相似性将相似的数据样本分组，而无需事先了解分组情况。通常，整个数据集中的簇总数是未知的。此类别中的算法示例包括K均值（K-Means）[3, 4]，带噪声应用的基于密度的空间聚类（Density-Based Spatial Clustering of Applications with Noise, DBSCAN）[5]，和模糊C均值（Fuzzy C-Means, FCM）[6]。可以采用多种方法来确定合适的值，例如肘部法（elbow method）、轮廓系数（silhouette score）、间隙统计（gap statistics），如第3.4节所讨论。

随着新应用的出现，对能够有效处理不同类型数据和场景的聚类算法的需求不断增长。同时，随着大数据和复杂数据结构（如高维、异构数据和大规模数据集）的兴起，需要适应性强的聚类算法来有效处理这些不同类型的数据。因此，聚类方法不断发展，因此全面调查和回顾现有文献以了解最新发展变得至关重要。几篇重要的综述对此做出了显著贡献。Rui Xu和Wunsch, D. [7]研究了计算机科学、机器学习和统计数据集的聚类技术。他们展示了如何在几个基准数据集上使用这些算法：旅行商问题和生物信息学——一个相对较新的主题，受到广泛关注。他们还讨论了簇验证、接近度测量和几个相关主题。Xu和Tian [8]在2015年进行了全面的聚类算法综述，涵盖了多种技术。作者根据其基本原理、特征和应用对这些算法进行了分类。综述包括对所有讨论算法的详细和全面的比较。Ezugwu等人[9]从更实际的角度提供了对各种领域中传统和前沿聚类算法的最新、系统和深入的分析。它涵盖了聚类在大数据、人工智能和机器人等多个领域的应用。该综述还重点关注聚类在教育、市场营销、医学、生物学和生物信息学等多个学科中所起的重要作用。上述三篇论文是自2000年以来关于聚类算法的最全面和被高度引用的研究。分别于2005年、2015年和2022年发表，这些工作对该领域做出了重大贡献。

除了这些开创性工作，其他一些重要作品主要关注聚类中的特定分类或应用。Bora等人[10]对模糊聚类算法和硬聚类算法进行了比较研究。重点是评估和对比这些聚类算法的性能，提供其优缺点的见解。Sisodia等人[11]探索了数据挖掘领域的各种聚类算法，强调了基本方面，如聚类基础、要求、分类、挑战及这些算法的应用领域。Rodriguez等人[12]提供了对9种著名聚类算法的全面比较分析。作者通过系统评估评估了这些算法的性能和特征，提供了对其优缺点的见解。这项研究有助于理解聚类方法，并根据特定应用需求做出明智选择。

在这项工作中，我们对现有的聚类算法文献进行了全面总结，并从四个不同的角度对其进行分类，以帮助用户有效识别适合其特定任务的算法。此外，我们讨论了当前的研究现状，并突出未来聚类技术的发展趋势。

2 方法

在本节中，我们描述了综述的方法，详细说明了用于收集出版物的关键词以及它们的筛选过程。我们定义了一组与我们主题相关的关键词，如“聚类”、“聚类算法”、“聚类方法”、“共识聚类”、“聚类技术”。创建关键词列表后，我们在三个信誉良好的学术数据库中进行了搜索，包括Google Scholar、arXiv和Scopus。我们使用布尔运算符（AND, OR）和截断来优化搜索查询。我们选择Google Scholar是因为它包括尚未正式发表的论文，如预印本。我们观察到，一些预印本出版物由于对研究领域的重大贡献，在早期阶段就获得了许多引用。然而，由于某些期刊在正式发表前需要较长的处理时间，这些出版物可能会长时间保持预印本状态。

我们根据以下标准筛选收集到的出版物：用英语撰写、在过去五年内发表、并且专注于新颖的聚类技术。此外，我们删除了与聚类算法不直接相关的重复论文，以确保剩余内容包括算法介绍、算法技术改进文章和应用文章。接下来，我们审查了标题、摘要和关键词，进一步筛选出版物以缩小选择范围。一旦我们集中在所选出版物的全文上，我们的目标是识别算法的基本原理、算法在其应用中的使用、实验程序和关键发现。我们考虑了实验设计、样本量和统计方法等方面，以评估结果的可靠性。最后，结果（在下一节中展示）综合了文献中发现的模式和趋势。

3 结果

在本节中，我们分析了聚类算法的基本特征和方法，并根据这些原理对算法进行分类，这也是目前最公认的分类方法。随后，我们从不同维度对算法进行分类，例如算法处理不同数据集大小的能力、数据点分配到簇的方式、预定义簇数量的要求和应用领域。此分类旨在指导用户根据特定的聚类任务选择合适的算法。算法分类系统的结构在图1中直观地展示。

3.1 根据基本原理和特征对算法进行分类

根据分组数据的基本特征和方法，聚类算法可以分为以下五个不同的子集[13–15]（总结在表1中）：

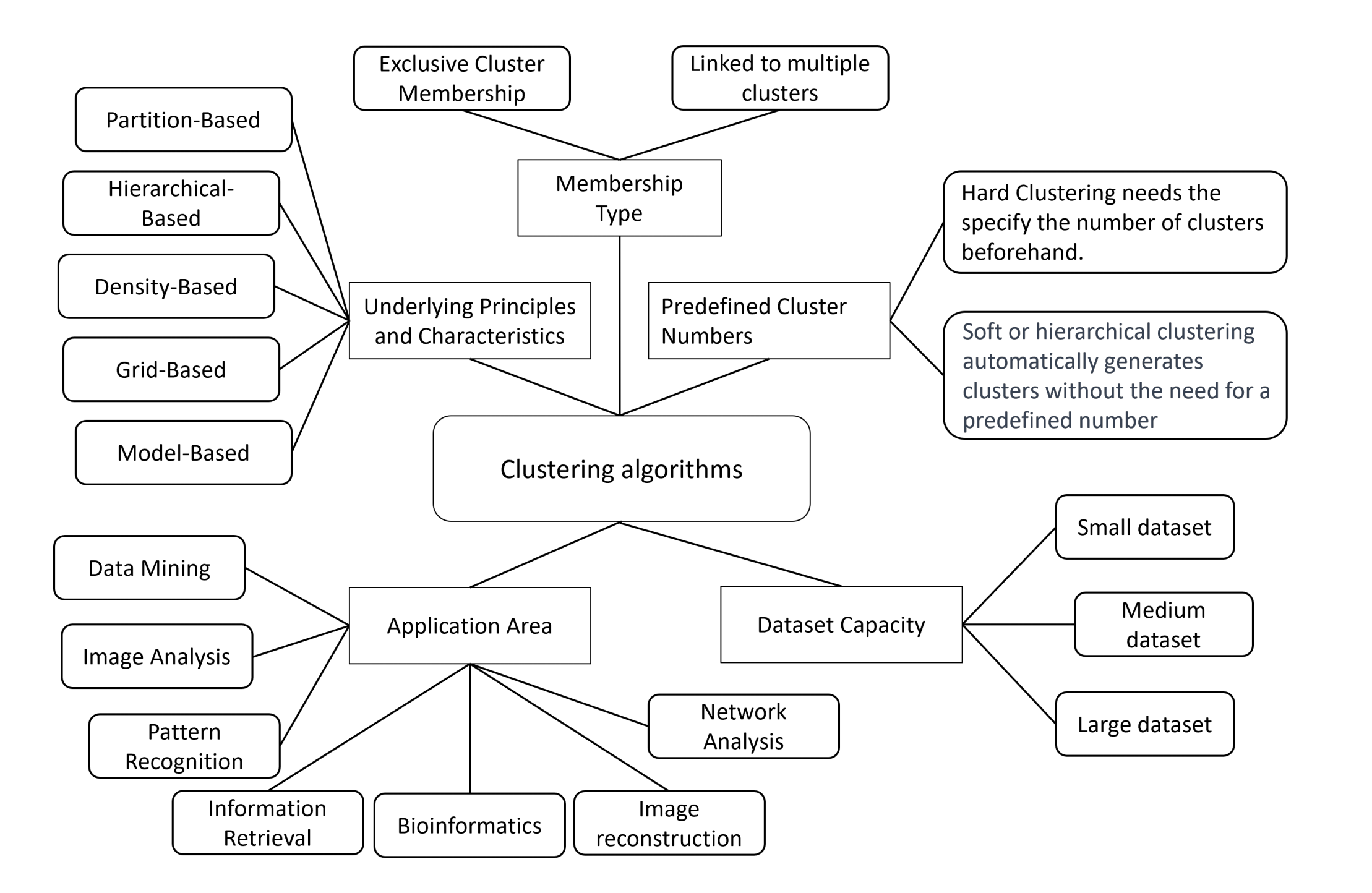
图1 聚类算法分类结构，涵盖五个维度

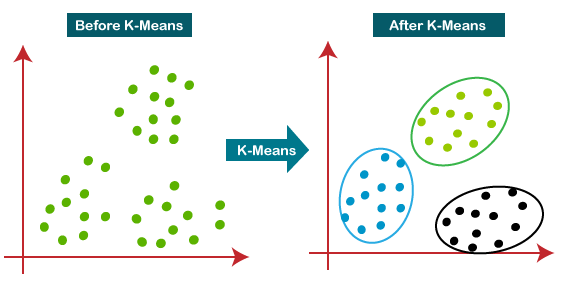
• 基于划分的聚类（例如，图2）：基于划分的聚类算法将数据划分为不重叠的簇。这些聚类算法的基本思想是将数据点的中心视为相应簇的中心，这通常具有较低的时间复杂度和较高的计算效率。然而，它们不适用于非凸数据，对离群点敏感，容易陷入局部最优，并且需要预定义簇的数量，这可能会影响聚类结果的性能。

图2 基于划分的聚类算法示例：左侧表示原始数据，右侧显示应用K-Means聚类算法后的结果簇。每个数据样本仅被分类到一个簇中。

• 基于层次的聚类（例如，图3）：层次聚类的唯一概念在于树状图的构建和分析。树状图是一种包含系统中所有数据点关系的树状结构。无需指定预定义的簇数量。这些算法可以处理各种形状和大小的簇。一旦构建了树状图，通过结构的水平切割可以在系统的最高层次定义单个簇。此切割下方的每个子分支代表一个独立的簇，将簇成员分配给每个数据样本。然而，层次聚类需要大量计算，特别是对于大型数据集，其时间复杂度通常高于其他聚类方法。这种结构对噪声和离群点敏感，如果处理不当，可能导致次优的簇。

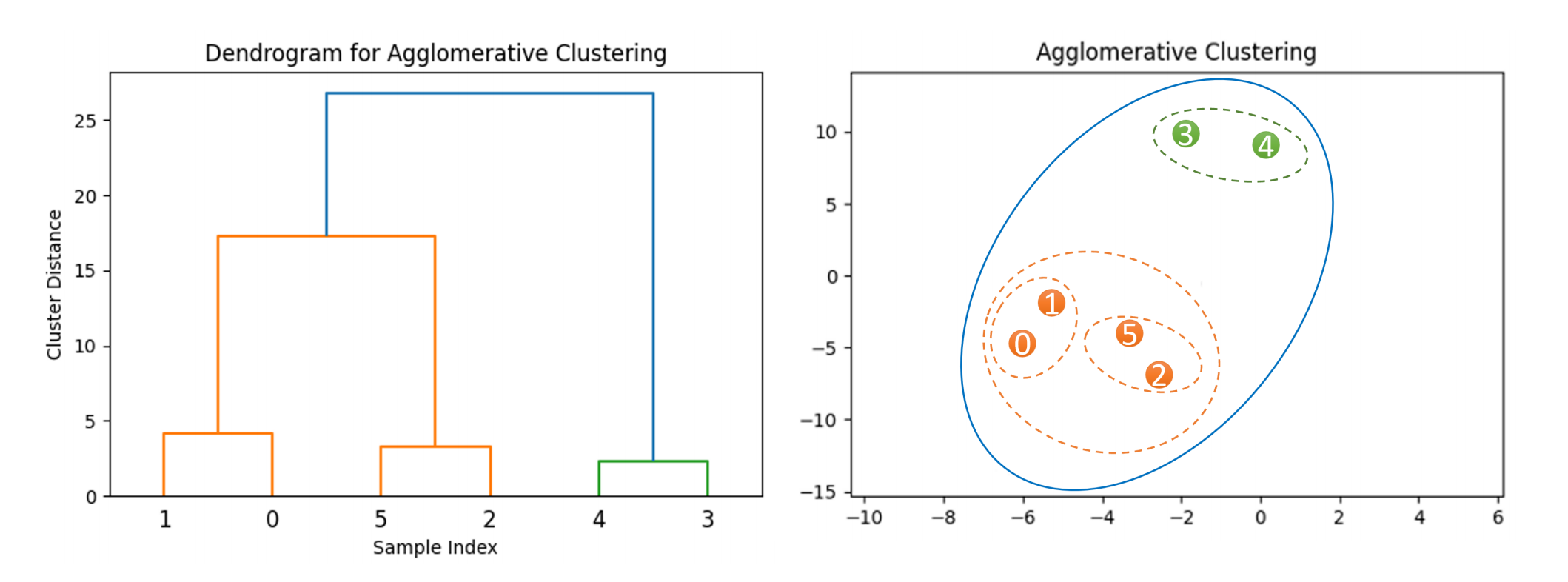
图3 层次聚类算法示意图：左侧显示了根据数据集中样本之间的关系构建的树状图，右侧展示了基于树状图的结果簇。

• 基于密度的聚类（例如，图4）：基于密度的算法旨在识别特征空间中高维区域的簇，同时将噪声点检测为离群点。这些算法具有高效的聚类效率，对参数敏感，适用于任意形状的数据集。在空间数据密度不均匀的情况下，聚类结果的质量会下降。此外，处理大型数据集时需要更高的计算资源。

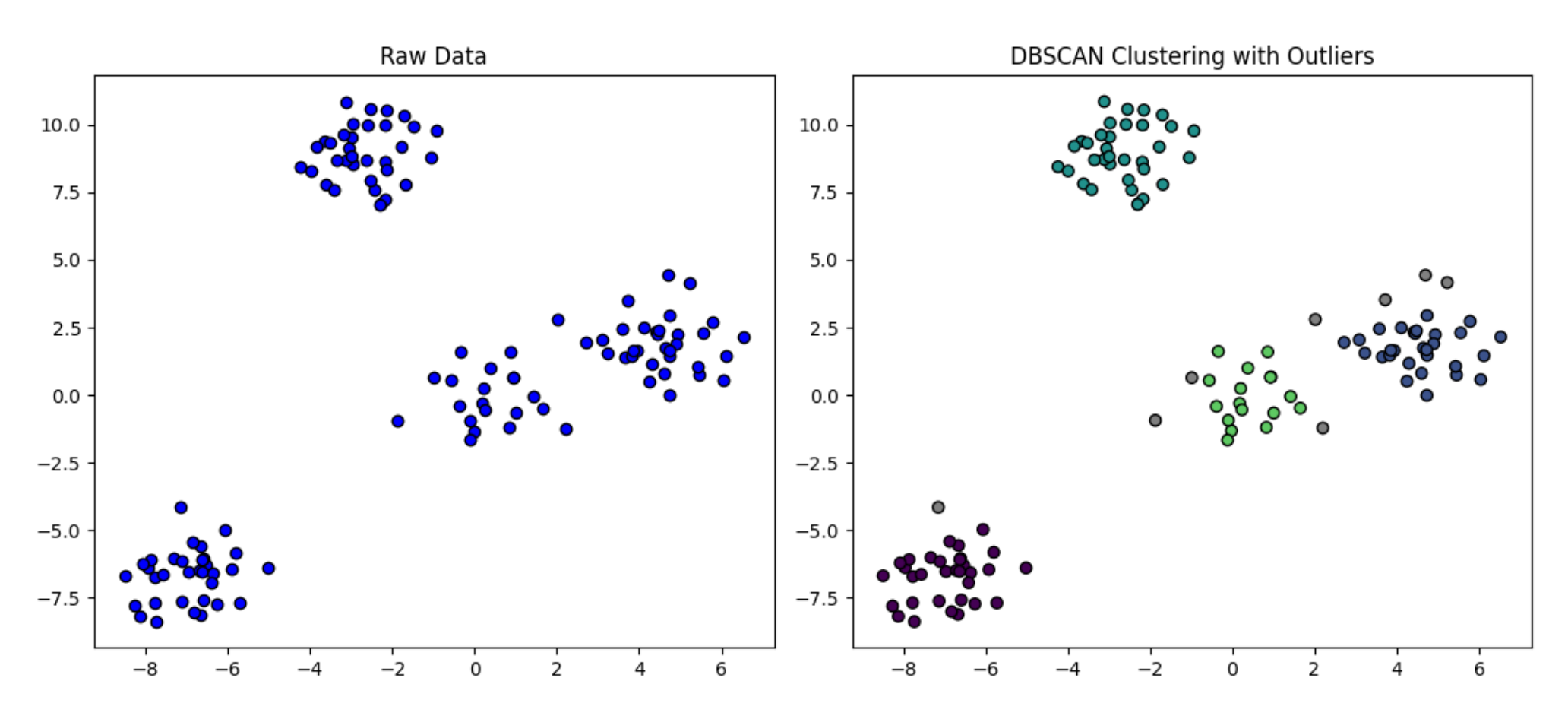
图4 基于密度的聚类算法示意图：左侧表示原始数据，右侧显示应用算法后的聚类结果。图中有一些离群点，用灰点表示。

• 基于网格的聚类（例如，图5）：这些聚类算法的基本原理是将初始数据空间划分为预定大小的网格结构进行聚类。尽管具有低时间复杂度、高可扩展性，并且兼容并行处理和增量更新，这些算法仍需考虑一些因素。聚类结果对网格大小非常敏感，追求更高的计算效率可能会以簇质量和整体聚类准确性为代价。

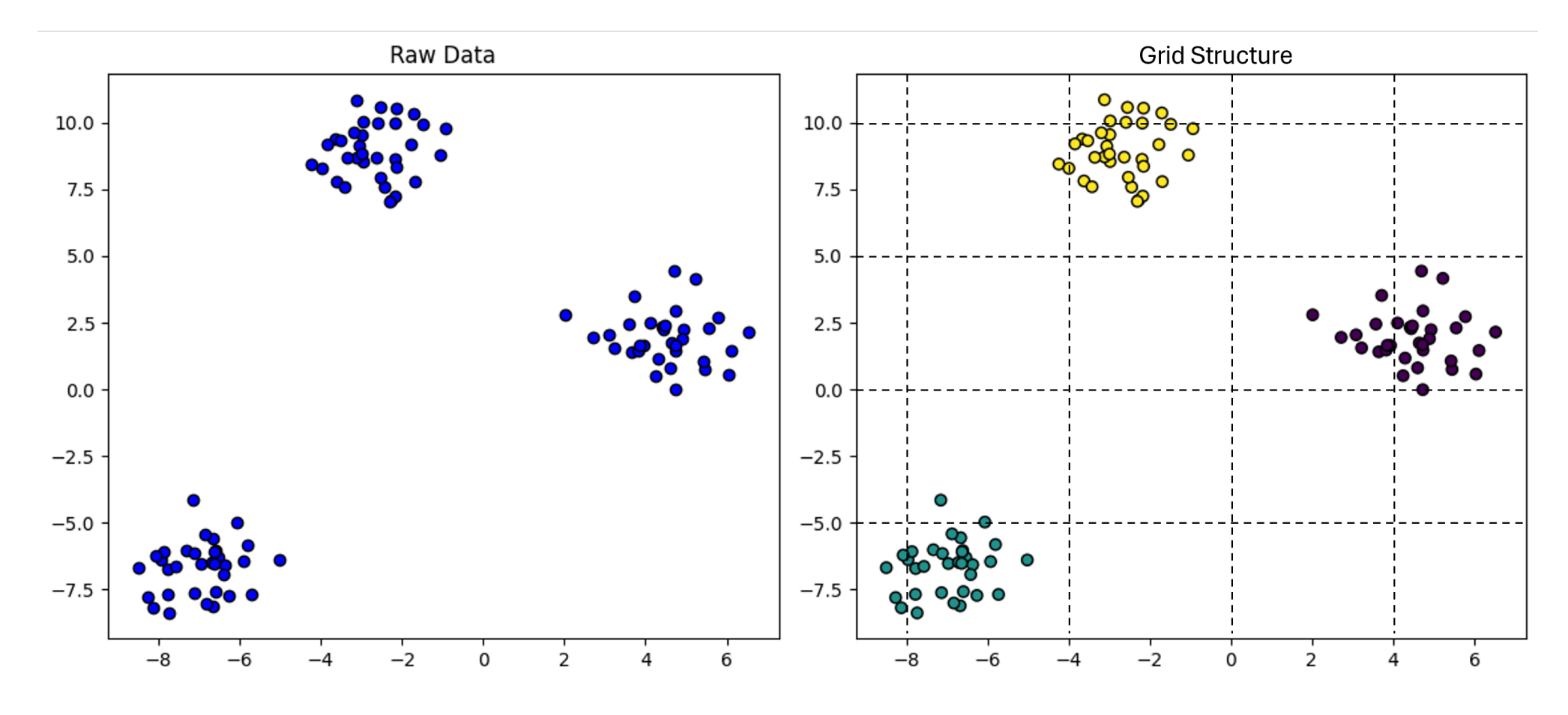
图5 基于网格的聚类算法示意图：左图表示原始数据，右图是网格算法示意图。网格可能允许任意形状或适应数据特征。簇的识别通常通过定义基于网格单元占据情况的规则或标准来完成。

• 基于模型的聚类（例如，图6）：基本思想是为每个簇选择一个特定模型，并找到该模型的最佳拟合。基于模型的聚类算法假设数据点是从概率模型生成的，并试图识别最合适的模型来解释数据分布。多样且成熟的模型提供了充分描述数据的方法，每个模型都有其独特的特性，在某些特定领域可能提供显著的优势。然而，总体而言，这些模型的时间复杂度相对较高，前提并不完全正确，并且聚类结果依赖于所选模型的参数。

图6 基于模型的聚类算法示意图。左侧表示原始数据，右侧显示应用高斯混合模型（GMM）后的聚类结果。由于不同的模型选择、参数设置和其他因素，实际的聚类结果可能会有所不同。

3.2 按数据点分配到簇的算法分类：单一 vs. 多重

聚类算法可以根据它们如何将数据点分配到簇中进行广泛分类。这导致了两种主要分类：硬聚类，其中每个数据点仅与一个簇相关联；软聚类，其中数据点可以同时与多个簇相关联。以下是每个类别中的一些经典算法。

• 硬聚类：K-Means、层次聚类（凝聚）、DBSCAN、OPTICS、K-Medoids、谱聚类（K路归一化切割）[39]、BIRCH。
• 软聚类：模糊C均值（FCM）、高斯混合模型（GMM）、可能性C均值（PCM）[40]、可能性模糊C均值（PFCM）[41]、核化模糊C均值（KFCM）[42]、层次模糊聚类（HFC）[43]。

3.3 按数据集容量分类的算法

算法在处理数据集大小的能力上有所不同，在本节中，我们根据其处理能力将所有算法分为三类。当然，定义什么是小型、中型或大型数据集在某种程度上是主观的，取决于具体任务的上下文。基于对Python开源库的概述和现有工作，我们根据处理能力将算法分为三组，如表2所示。

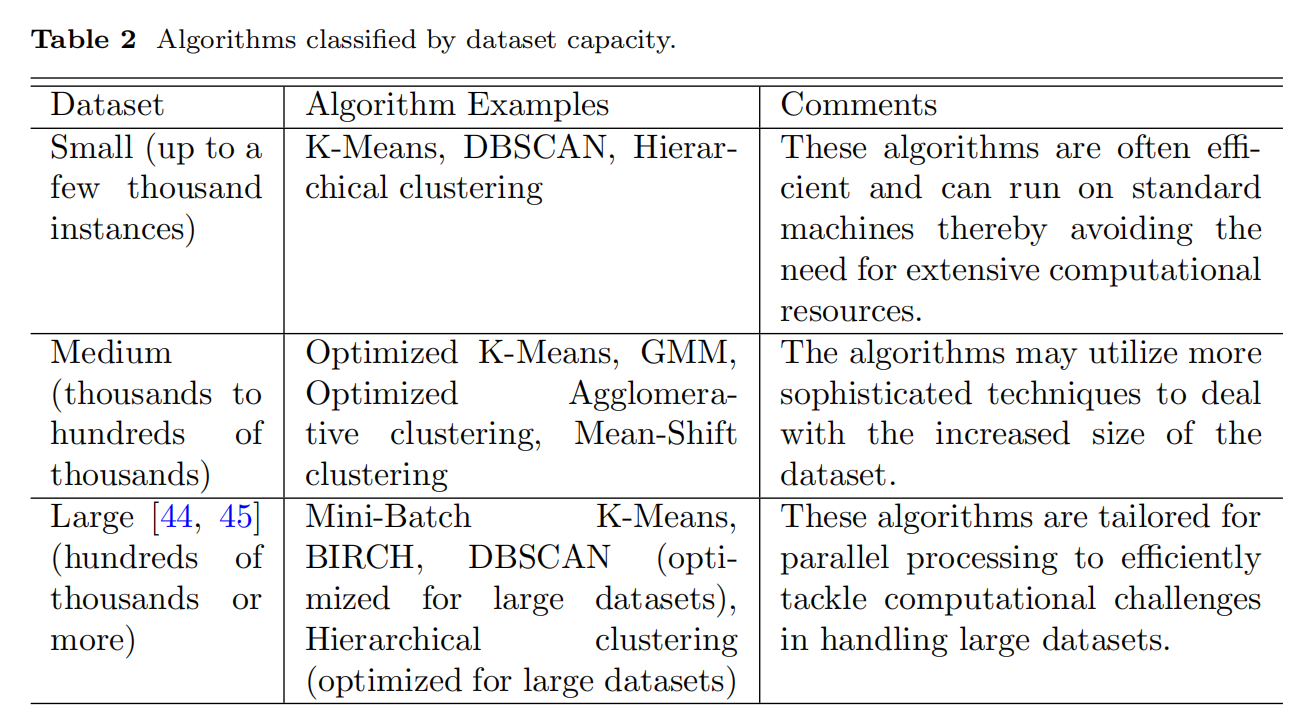
• 小型数据集：通常，小型数据集可能包含几百到几千个实例。这是一个可以轻松加载到内存中并处理而不需要显著计算资源的规模。
• 中型数据集：中型数据集的范围可能从几千到数万个实例。与小型数据集相比，它可能需要更复杂的算法和计算资源，但仍然是可管理的。
• 大型数据集：大型数据集通常包含数十万到数百万（或更多）实例。处理此类数据集通常需要专门的算法、分布式计算或并行处理，因数据量庞大。

3.4 按预定义簇数分类的算法

并非所有的聚类算法都需要预定义簇的数量。主要有两种类型的聚类算法：

• 硬聚类：此类别中的算法（如K-Means）要求用户事先指定簇的数量。
• 软聚类或层次聚类：使用层次聚类或高斯混合模型（GMM）等算法时，不需要提前指定簇的数量。聚类可以在不同的粒度或簇数量级别上进行，您可以在事后选择使用哪种级别。

硬聚类中最大的挑战是如何确定最优的簇数。聚类结果可以根据使用的簇数、在数据中发现的模式粒度以及解决方案的实用性进行不同的解释。作为聚类过程中的关键步骤，选择正确的簇数量也会影响分析得出的见解以及聚类组在实际情况中的有用性。有一些方法可以用来确定最优的簇数。

• 肘部法：运行聚类算法以获取一系列簇数，并将簇内平方和（惯性）与簇数绘制成图。寻找图中的“肘部”，即惯性减少的速度减慢的点。这个点通常被认为是最优的簇数。有多篇文献使用肘部法来确定最优簇数[46–48]。
• 轮廓系数：指一种解释和验证数据簇内一致性的方法。轮廓系数测量一个对象与其自身簇的相似度与其与其他簇的相似度。选择使轮廓系数最大的簇数。有多篇文献使用轮廓系数来评估最优簇数[49–51]。
• 间隙统计[52]：将数据集上的聚类性能与随机数据集（或较少簇数）上的性能进行比较。最优簇数应具有比随机聚类更大的性能差距。有一些文献使用间隙统计来确定簇数[53–55]。
• 层次聚类中的树状图[56]：如果任务适用于层次聚类算法，可视化树状图并寻找切割它以得到合理数量的独立簇的级别。有一些文献使用树状图进行聚类[57, 58]。

3.5 按应用领域分类的算法

在本节中，我们将比较各个主要应用领域中主要使用的聚类算法，如表3所示。在数据挖掘和信息检索等领域，K-Means和DBSCAN等算法因其处理大型数据集的效率而被频繁使用。相比之下，图像分析和生物信息学等领域通常依赖于谱聚类和层次聚类等算法，这些算法更适合这些领域的复杂模式和结构。值得注意的是，像AutoClass[59]和Superpixel[60]这样的新算法在特定复杂场景中表现良好。

4 评价指标

虽然大多数数据集缺乏聚类算法的真实标签，但仍有方法可以评估聚类质量。评价指标对于指导聚类算法的开发、选择和优化至关重要，使过程更加系统和有依据。在聚类过程中，数据样本会转化为高维空间中的向量。这些向量之间的距离复杂地反映了整体相似性，包含了数据样本中的所有相关特征。因此，“点之间的距离”在形成簇时至关重要，并作为评估聚类性能的常见标准。这一概念指的是个体数据点之间的相异或相似的数值度量，通常基于数据特征计算。典型的度量包括欧几里得距离、曼哈顿距离或文本数据的余弦相似度。

图7展示了K-Means聚类的一个示例，展示了数据点之间的距离。图中描绘了两种类型的距离：一种表示簇内数据样本之间的距离（蓝色和橙色虚线），另一种表示不同簇中心之间的距离（绿色虚线）。簇内数据点之间的距离明显小于数据点与其他簇中心之间的距离。

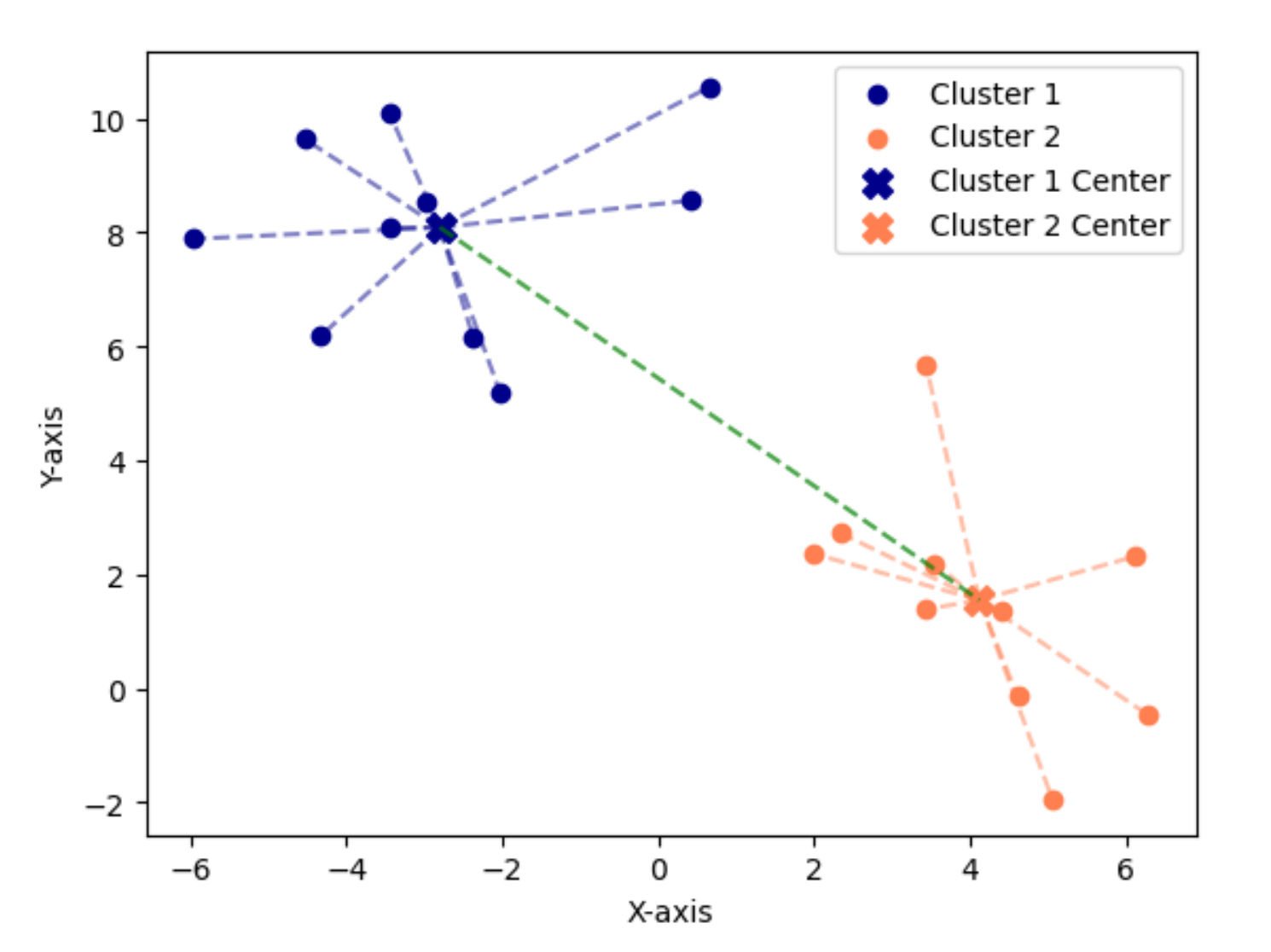
图7 K-Means聚类示例，包含两个簇，展示了数据点之间的两种不同距离类型。

通过强调评价指标的重要性和点之间距离的作用，评估和改进聚类算法的过程变得更加稳健和有意义。评价指标分为内部和外部类型。内部指标仅基于固有数据信息评估簇的质量，关注簇内数据样本的紧密性（凝聚力）和簇之间的独特性（分离度）。示例包括轮廓系数、Davies-Bouldin指数、Dunn指数和惯性（用于K-Means）。外部指标需要真实类别标签，通过使用精度、召回率和互信息来评估与已知标签的一致性。例如调整兰德指数（ARI）、归一化互信息（NMI）、Fowlkes-Mallows指数、精度、召回率和F1分数。内部指标专注于内在属性，而外部指标依赖于真实标签评估算法准确性。选择取决于数据的可用性和聚类目标。

4.1 内部评价指标

聚类算法的内部评价指标可以仅基于数据的内在特性和聚类算法的结果评估簇的质量，而不使用任何外部信息，如真实标签。这些指标可以定量地测量聚类质量的各个方面，如紧密性、分离度和方差。在选择和解释这些指标时，考虑数据的具体特性和聚类任务的目标至关重要。

4.1.1 轮廓系数

轮廓系数是一种广泛使用的内部评价指标，用于评估无监督聚类算法产生的簇的质量。它衡量簇的分离程度，并提供聚类解决方案适当性的指示。单个数据点的轮廓系数计算为数据点与同簇其他点的平均距离（a）与数据点与最近邻簇点的平均距离（b）之差，除以a和b中的最大值。对于数据点i，公式为：

S ( i ) = b ( i ) − a ( i ) max ⁡ { a ( i ) , b ( i ) } S(i) = \frac{b(i) - a(i)}{\max \{a(i), b(i)\}} S(i)=max{a(i),b(i)}b(i)−a(i)​

轮廓系数范围从-1到1，值越高表示簇定义越好。接近1的分数表示数据点与其自身簇匹配良好，与邻近簇匹配较差，表明聚类效果好。接近0的轮廓系数表示簇之间重叠。接近-1的轮廓系数表示数据点可能分配到了错误的簇。聚类解决方案的总体轮廓系数是所有数据点轮廓系数的平均值。

4.1.2 Davies-Bouldin指数

Davies-Bouldin指数是一种用于评估聚类解决方案质量的指标。它衡量簇的紧密性和分离度，旨在找到彼此分离良好的簇。Davies-Bouldin指数的公式为：

$$DBI=\frac{1}{n_c}\sum _{i=1}^{n_c}\underset{i\ne j}{\max }\left(\frac{{\text{avg-radius}}_i+{\text{avg-radius}}_j}{\text{distance}(c_i,c_j)}\right)$$

其中，$ n_c $ 是簇的数量，$ c_i $ 和 $ c_j $ 是簇i和簇j的质心，$ \text{avg-radius}_i $ 和 $ \text{avg-radius}_j $ 是从质心到簇i和簇j中点的平均距离，$ \text{distance}(c_i, c_j) $ 是簇i和簇j质心之间的距离。

Davies-Bouldin指数基于欧几里得距离，假设簇具有球形形状，在处理不规则形状的簇时可能表现不佳。此外，公式假设簇大小相等，因此可能不适用于簇大小不平衡的数据集。如果聚类算法产生不同数量的簇，或者簇的真实数量未知，可能表现不佳。尽管存在这些限制，当假设与数据特征和聚类分析目标一致时，Davies-Bouldin指数仍然是一个有用的工具。

4.1.3 Dunn指数

Dunn指数关注簇的紧密性和分离度。它旨在在最小化簇内直径（点之间的最大距离）和最大化簇中心之间的距离之间找到平衡。该指数定义为最小簇间距离与最大簇内直径的比率。

$$DI=\frac{{\min }_{i\ne j}\text{distance}(c_i,c_j)}{{\max }_{1\le k\le n}\text{diameter}(C_k)}$$

其中，$ n $ 是簇的数量，$ C_i $ 和 $ C_j $ 是簇，$ \text{diameter}(C_i) $ 是簇 $ C_i $ 内的最大距离，$ \text{distance}(c_i, c_j) $ 是簇中心 $ c_i $ 和 $ c_j $ 之间的距离。

Dunn指数对异常值敏感，并且高度依赖于距离度量。它假设簇是球形的，因此如果簇具有非球形形状，可能无法准确反映簇之间的真实分离。Dunn指数产生数值结果，但其作为“好”或“坏”的解释是主观的，并且在聚类问题中取决于具体情境。尽管存在这些缺点，Dunn指数在谨慎使用并结合其他评价指标时，仍然是一个有价值的工具。

上述三种是常用的评价指标，还有其他不太流行的评价指标，例如Calinski-Harabasz指数[61]，它评估簇间方差与簇内方差的比率，值越高表示簇定义越好。惯性（簇内平方和）[62]，它测量数据点与其簇中心之间的平方距离之和，惯性越低表示簇越密集、越紧凑。间隙统计[52]，它将数据集的聚类质量与参考随机数据集的聚类质量进行比较，间隙越大表示聚类效果越好。CH指数（Cophenetic相关系数）[25]，它测量树状图中Cophenetic距离与原始距离之间的相关性，CH指数越高表示聚类效果越好。

4.2 外部评价指标（当真实标签可用时）

4.2.1 调整兰德指数 (ARI)

调整兰德指数 (ARI) 是聚类分析和机器学习中广泛使用的评价指标，用于评估两个聚类解决方案之间的相似性。它测量真实类别标签和聚类算法分配的标签之间的一致性，并校正了随机因素的影响。ARI 的公式如下：

$$\text{ARI}=\frac{\text{RI}-\text{Expected RI}}{\max (\text{RI})-\text{Expected RI}}$$

其中，RI 是兰德指数，测量真实聚类和预测聚类之间的一致性（包括同簇和不同簇的情况）。Expected RI 是在随机聚类假设下的期望兰德指数，表示随机聚类情况下的 RI 期望值。分母中的 max(RI) 表示兰德指数的最大可能值，将 ARI 归一化到 [-1, 1] 范围内。

ARI 的局限性如下：

• 对不平衡簇大小的敏感性：ARI 对不平衡簇大小敏感。如果不同簇中的样本数量差异显著，ARI 可能偏向于较大的簇。

• 依赖簇数量：ARI 假设知道真实的簇数量。如果真实簇数量未知或聚类算法产生不同数量的簇，ARI 可能无法提供准确的评价。

• 随机聚类假设：ARI 的随机校正假设簇分配是随机进行的。在某些情况下，特别是对于某些聚类算法或数据类型，这一假设可能不成立。

• 仅限于成对比较：ARI 设计用于成对聚类比较，无法提供关于多个簇整体结构的信息。它可能无法捕捉数据中的更复杂关系。

• 依赖真实标签：ARI 需要真实类别标签，在无监督学习场景中可能无法获得。在这种情况下，可能需要使用其他评价指标。

尽管存在这些局限性，ARI 仍然是广泛使用且易于解释的聚类评价指标。在具体聚类任务中考虑这些缺点，并相应选择评价指标是很重要的。

4.2.2 归一化互信息 (NMI)

归一化互信息 (NMI) 提供了一个定量指标，用于衡量真实类别标签和聚类算法分配的标签之间的一致性，考虑了精度和召回率，提供了对聚类解决方案质量的平衡视角。

NMI 的公式如下：

$$\text{NMI}=\frac{2\cdot I(Y;C)}{H(Y)+H(C)}$$

其中，Y 是真实类别标签集合，C 是算法分配的簇标签集合，I(Y ; C) 是 Y 和 C 之间的互信息，H(Y) 和 H© 分别是 Y 和 C 的熵。

NMI 的取值范围从 0 到 1，0 表示没有互信息，1 表示真实标签和预测标签之间完全一致。较高的 NMI 表示在捕捉底层类别结构方面更好的聚类解决方案。NMI 是大多数聚类解决方案中常用的指标，因为它在聚类评价中同时考虑了同质性和完整性，并且归一化有助于在不同大小的数据集之间进行比较。

NMI 的局限性在于它假设每个簇对应一个单一类别，这在实际数据中可能并不总是成立。

5 讨论

近年来，聚类算法研究的重点从单纯改进底层算法转向在特定领域的应用。这一转变是由于各个领域中数据挑战的多样性和复杂性日益受到重视。研究人员现在积极探索如何有效地应用和调整聚类算法，以满足生物信息学、医疗保健、自然语言处理、图像和视频处理、社交网络分析、网络安全和异常检测等领域的独特需求。研究社区集中精力定制聚类解决方案，以适应特定应用环境，从而在领域特定的聚类方法应用中取得了显著进展。我们观察到，COVID-19 大流行导致 2021 年至 2022 年间医疗影像和医疗保健中聚类算法的使用显著增加。在深度学习技术迅速发展的背景下，聚类算法的发展趋势愈发明显。特别是，越来越多地将神经网络等深度学习技术整合到聚类算法中，以提高其性能，特别是在处理高维和复杂数据时。K-Means 是最古老和最知名的聚类算法之一，因其简单性和在基于相似性划分数据方面的有效性而广受欢迎。尽管历史悠久，K-Means 仍然在各种应用中广泛使用，并在聚类技术文献中占有一席之地。它常作为基准方法与新提出的方法进行比较，并且不断有改进其性能的努力。另一个值得注意的趋势是混合聚类方法的日益流行。这些方法结合了不同的聚类算法或将聚类与其他机器学习技术相结合，旨在利用多种方法的优势以提高性能。

当前，聚类算法面临的主要挑战是确定最佳簇数。现有技术生成的组通常表现出模糊的簇，即数据被分组到未知原因的未指定类别中。如果只有一个组存在，可以将其分类为异常值，但有时多个组仍未被识别。这突显了算法分组数据与人类对这些组的主观解释之间的潜在差异。在最近的学术文献中，几种不同的聚类方法被频繁使用，各有其优点和应用。因此，聚类方法的选择高度依赖于任务。没有一种方法能够在所有类型的数据和应用中普遍胜出。我们的综述从多个角度对算法进行分类，可以帮助用户选择适合特定应用的聚类算法。