推断统计——抽样分布、中心极限定理和置信区间
目录
一、介绍
二、 抽样分布
2.1 例子
2.2. 样本比例的抽样分布
三、中心极限定理
四、 置信区间
4.1 要点:
4.2 例子:
五、 比例和平均值推断的条件
一、介绍
统计学领域包括描述和建模变异性的方法以及在存在变异性时做出决策的方法。在推论统计中,我们通常希望对某个总体做出决策。总体是指我们希望得出结论或做出决策的宇宙中所有元素的测量值集合。
在大多数统计学应用中,可用数据均来自从感兴趣的范围中选择的单位样本。
二、 抽样分布
假设我们有一个总体,其总体参数为 (µ,σ)。我们可能不知道总体参数,甚至可能不容易找到总体参数。因此,我们尝试通过抽取大小为 n 的样本来估计总体参数,并计算用于估计参数的统计数据。
如果我们再次随机抽取大小为 n 的样本,然后再次计算统计数据,我们很可能会得到不同的值。
那么,我们可以得到的统计数据的分布是什么样的呢?对于试图估计总体参数的统计数据,我可以得到不同值的频率是多少呢?这个分布就是抽样分布。
2.1 例子
假设我们有一个包含三个数字的总体——1、2 和 3。总体的平均值(用 µ 表示)为 (1+2+3)/3,即 2。现在,我们从总体中随机抽取大小为 2 的样本,并每次报告样本统计量,即样本的 x̅。
| 已选 # 人 | 腳 |
| 1,1 | 1 |
| 1,2 | 1.5 |
| 1,3 | 2 |
| 2,1 | 1.5 |
| 2,2 | 2 |
| 2,3 | 2.5 |
| 3,1 | 2 |
| 3,2 | 2.5 |
| 3,3 | 3 |
2.2. 样本比例的抽样分布
假设我们有一个大碗,里面有 10,000 个不同颜色的球,其中 60% 是黄色的球。那么总体参数就是 p = 0.6。假设 Y 是一个随机变量,当我们从碗里取出一个黄色球时,取值为 1,当我们取出一个不同颜色的球时,取值为 0。显然,Y 服从伯努利分布。Y 的平均值和标准差分别为 0.6 和 0.49。
假设 X 是另一个随机变量,表示 10 条独立伯努利轨迹的总和。X 的均值和方差为 10×0.6 = 6,标准差为 1.55

请注意,如果 np >= 10 且 n(1-p) >= 10,则样本比例的抽样分布近似于正态分布。
三、中心极限定理
中心极限定理 (CLT) 指出,假设所有样本的大小相同,并且不管总体分布形状如何,样本均值的分布随着样本量变大而趋近于正态分布。也就是说,当一个随机变量(可以是任何随机变量,不一定是我们在前面的例子中采用的二项式随机变量)的抽样分布的均值绘制在频率分布曲线上时,它趋近于正态分布
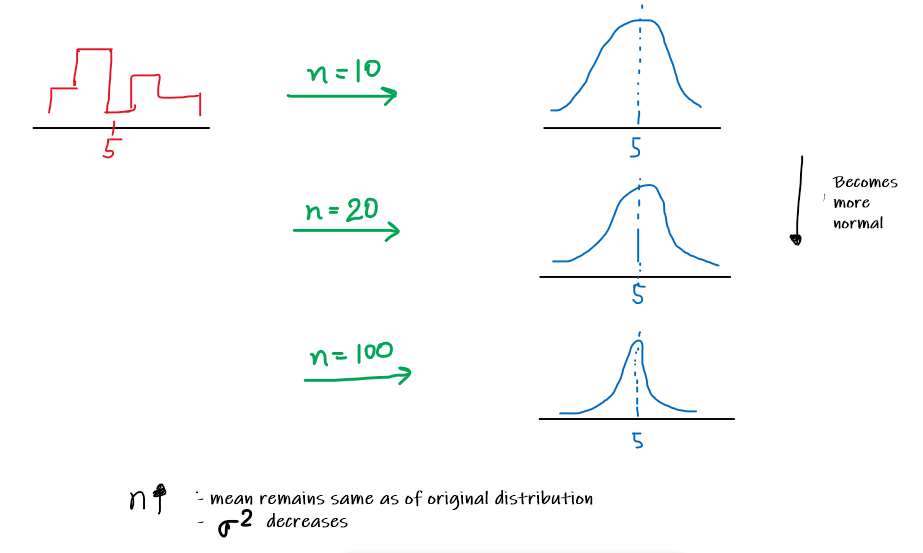
需要注意以下几点:
1. CLT 指出,随着样本量增大,样本均值的分布趋近于正态分布
2. 样本量 >= 30 被认为足以使 CLT 保持
3.

四、 置信区间
假设有10万选民,有2个候选人A和B参加选举。我们想知道候选人A赢得选举的可能性。
由于总体比例(即支持 A 的比例)未知,为了估计总体比例,我们从总体中抽取许多样本(样本量为 n = 100)并计算每个样本的样本比例。
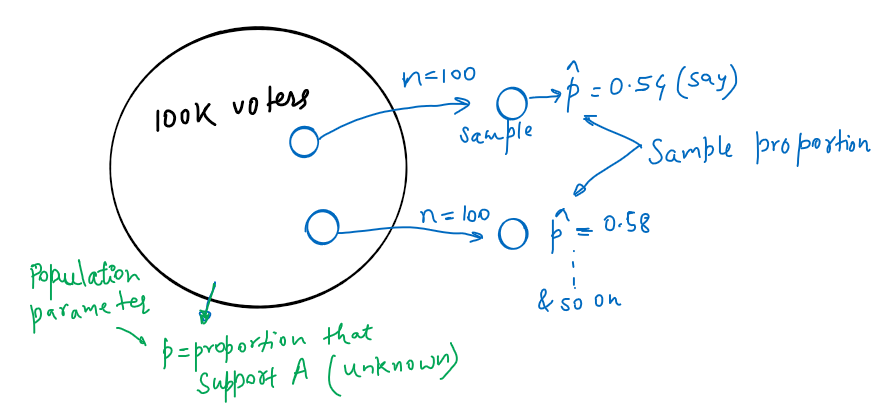
由于我们的样本量比总体小得多(远低于 10%),我们可以假设我们询问的每个人对 A 和 B 的偏好大致是独立的。我们实际上不知道实际的总体参数是什么(即 p)。
因此,对于第一种情况,即 n = 100 和 p-hat = 0.54,我们可能会得到各种结果。样本比例 p-hat = 0.54 可能高于“p”(总体参数)或低于 p。我们之所以有这种不确定性,是因为我们实际上不知道实际的总体比例(参数)是多少。

现在,我们感兴趣的是 - p-hat = 0.54 在 p 的 2 个标准差内的概率是多少?(即 95%)即,如果我取 100 个样本并计算样本比例,那么 95% 的时间在 2 个标准差内的概率是多少。
由于 p 未知,无法计算样本比例的标准差。相反,我们将计算样本比例的标准误差
因此,对于 95% 的置信度,

它将产生间隔(并且间隔不会总是相同,因为它取决于我们的样本比例),其中将包括真实比例,即 95% 的人口比例“p”。
如果我们想要缩小间隔,即我们必须降低误差幅度,即我们必须增加 n(样本大小),因为标准误差与 n 成反比。
因此,我们用置信区间来回答的问题是:对于任何给定的估计值(样本),我们对该样本周围的一定范围实际上包含真实的人口比例有多大信心?
4.1 要点:
1. 置信度“水平”是指该方法的长期成功率,即这种间隔捕获感兴趣的参数的频率。
2. 特定的置信区间为感兴趣的参数提供了一系列合理的值。
3. 误差幅度越大,置信区间越宽,越有可能包含感兴趣的参数(置信度增加)
4. 增加置信度将会增加误差幅度,从而导致区间变宽。
4.2 例子:
假设一位棒球教练对他所在联盟的快球投球的真实平均速度感到好奇。教练随机记录了 100 次投球中每个快球的速度(以公里/小时为单位),并为平均速度建立了 95% 的置信区间。结果区间为 (110,120)。我们能否说真实平均值在 110 到 120 公里/小时之间的概率为 95%?
在这种情况下,我们不会说这个特定区间包含真实平均值的概率为 95%,因为这意味着平均值可能在这个区间内,也可能在其他地方。这种表述让人觉得总体平均值是可变的,但事实并非如此。这个区间要么捕捉到了平均值,要么没有。区间因样本而异,但我们试图捕捉的总体参数不会改变。
更安全的说法是,我们有 95% 的信心认为这个区间捕获了平均值,因为这种表述更接近于置信水平的长期捕获率。
五、 比例和平均值推断的条件
1. 随机条件:随机样本为我们提供了来自总体的无偏数据。当样本不是随机选择的,数据通常会有某种形式的偏差,因此使用非随机选择的数据来推断总体可能会有风险。
2. 正常条件:只要成功和失败的预期次数都至少为 10,p-hat 的抽样分布就近似于正常。当我们的样本量 n 相当大时,就会发生这种情况。
因此,预期成功:np >= 10 预期失败:n(1-p) >= 10
如果我们正在建立置信区间,我们没有可以插入的 p 值,因此我们改为计算样本数据中观察到的成功和失败次数,以确保它们都至少为 10。
3. 独立性条件:要使用 p-hat 标准差公式,我们需要独立的个体观测值。当我们进行无放回抽样时,个体观测值在技术上并不独立,因为移除每个项目都会改变总体。
但 10% 条件表示,如果我们抽样 10% 或更少的总体,我们可以认为个别观察结果不会显著改变总体。这使我们能够使用 p-hat 标准差公式。

在显著性检验中,我们使用样本大小n和假设值p。
如果我们要为 p 建立置信区间,我们实际上并不知道 p 是什么,因此我们用 p-hat 代替 p 的估计值。当我们这样做时,我们称之为 p-hat 的标准误差,以区别于标准差。因此,p-hat 标准误差的公式为


