当前位置： 首页 > news >正文

【查找算法概念】与【线性表的相关查找算法】

news 2025/4/21 16:25:37

1.知识回顾

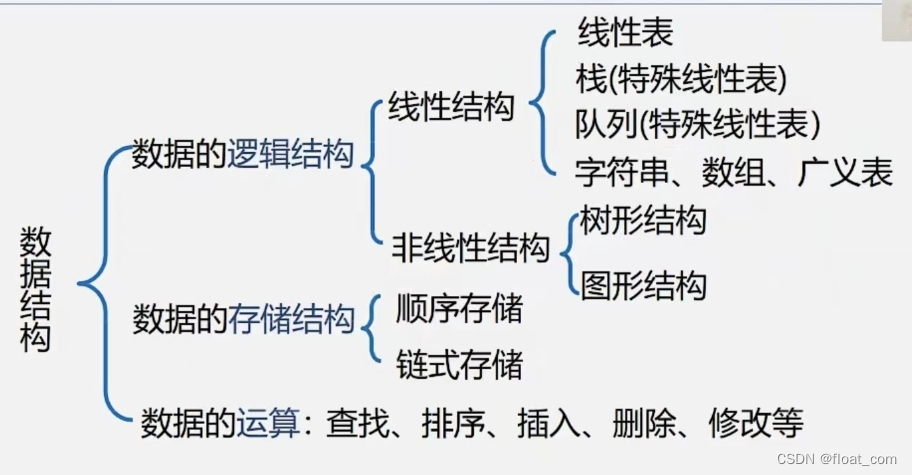
在这里插入图片描述

2.查找算法相关问题汇总

2.1在哪里查找

查找表

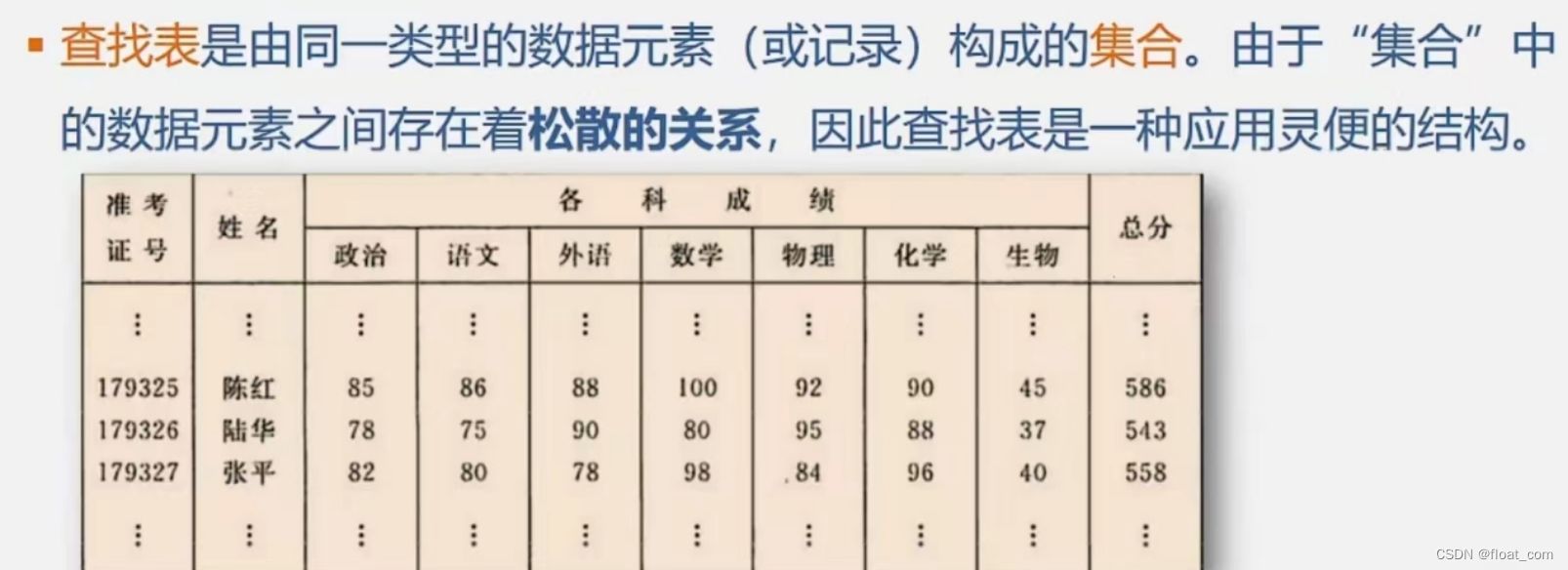
在这里插入图片描述

2.2通过什么进行查找

关键字的对应
在这里插入图片描述
主关键字：比如我们可以通过一个学号来唯一确定一名学生
这里的学号就是一种主关键字。

次关键字：而通过一个名字李华，我们可能会确定不止一名学生
这里的名字李华就是一种次关键字。

实际上我们只需要明白
主关键字唯一确定一个元素
次关键字可能确定多个元素
即可

2.3查找是否成功

在这里插入图片描述

2.4查找的目的

在这里插入图片描述

2.5查表找的分类

在这里插入图片描述

2.6评价查找算法–平均查找长度

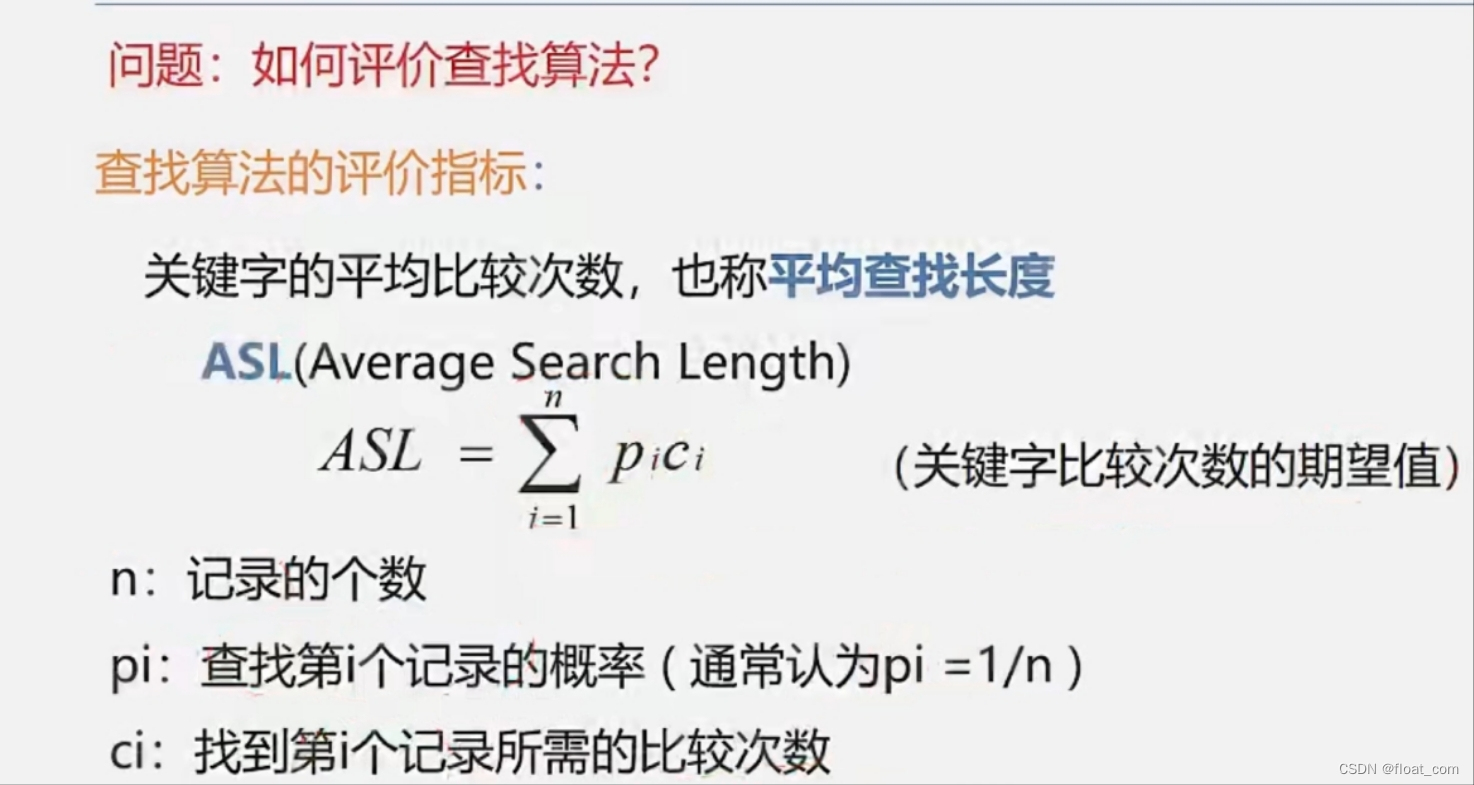
在这里插入图片描述

2.7查找过程中的研究目标

在这里插入图片描述

3.线性表的查找

3.1分类：

顺序查找（线性查找），折半查找（二分或对分查找），分块查找

3.2线性表的顺序查找

实际上就是暴力遍历，从表头遍历到表尾，直至查找到对应元素
当然我们也可以从表尾遍历到表头直至查找到对应元素

3.2.1顺序查找的应用范围：

  • 顺序表或线性链表表示的静态查找表
  • 表内元素之间可以无序

3.2.2顺序表的表示

//定义动态顺序表初始默认最大容量
#define InitSize 12typedef int KeyType ;
//KeyType:是顺序表中每个关键字的类型//1.顺序表的表示：//1.1数据元素类型定义
typedef struct
{KeyType key;//关键字域//除了关键字域以外，还可以定义其他域
}ElemType;//ElemType:是顺序表中的数据类型//1.2顺序表的结构类型定义typedef struct 
{ElemType * elem;//顺序表的基地址（动态数组存储）int length;//表长int maxsize;//顺序表的最大容量
}SSTable;//SSTable:用来定义一个顺序表

3.2.3 顺序表的顺序查找算法：

  • 1.一般的顺序查找算法：
    在这里插入图片描述
三种基本形式的代码
//在顺序表L中,查找值为key的数据元素，若成功返回其位置信息，否则返回0；
//注意这里的位置信息就是顺序表数组下标：从1开始（因为我们是从下标1开始存储第一个有效数据的）//1.不带监视哨的顺序查找法
//思路：从后往前比较，直到找到key或比较到最后一个元素
//时间复杂度：O(n)
//空间复杂度：O(1)//方式1：
int Search1(SSTable L, KeyType key)
{for (int i = L.length; i >= 1; i--){if (L.elem[i].key == key){return i;}}return 0;
}//其他方式：（主要包含了边界条件的判断）
//方式2：
int Search2(SSTable L, KeyType key)
{int i;for (i = L.length; L.elem[i].key!=key; i--){if (i <= 0){break;}}if (i > 0){return i;}else{return 0;}}//方式3：
int Search3(SSTable L, KeyType key)
{int i;for (i = L.length; L.elem[i].key != key && i > 0; i--);//这里实际上就是将两个判断条件合并了 一定要注意这里的for循环没有循环体，需要加引号。if (i > 0){return i;}else{return 0;}}
  • 改进过后的顺序查找（添加了监视哨）：
    在这里插入图片描述
    如下图：
    在这里插入图片描述
    代码如下：
//2.改进后带监视哨的顺序查找法
//思路：把待查关键字key存入表头（哨兵，监视哨）从后往前比较，直到找到key或比较到最后一个元素，直接返回i的值
//可以减少查找过程中每一步都要检测是否查找完毕，加快了查找速度int Search4(SSTable L, KeyType key)
{//[1]初始化监视哨L.elem[0].key = key;//[2]顺序查找操作：int i;for ( i = L.length; L.elem[i].key != key; i--);//[3]返回最后的i值：//如果能找到key，那么i就是key的位置，否则i就是0（即监视哨位置的下标）return i;
}

3.2.4顺序查找法操作一览：

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>//定义动态顺序表初始默认最大容量
#define InitSize 12typedef int KeyType ;//KeyType:是顺序表中每个关键字的类型//1.顺序表的表示：//1.1数据元素类型定义
typedef struct
{KeyType key;//关键字域//除了关键字域以外，还可以定义其他域
}ElemType;//ElemType:是顺序表中的数据类型//1.2顺序表的结构类型定义typedef struct 
{ElemType * elem;//顺序表的基地址（动态数组存储）int length;//表长int maxsize;//顺序表的最大容量
}SSTable;//SSTable:用来定义一个顺序表//2.顺序表的一些基本操作：（与之前所学完全一致）
//这里仅涉及初始化，与输出（重点是查找算法）//2.1顺序表的初始化（动态顺序表）
bool InitSeqList(SSTable* L)
{//[0]防止程序潜在异常if (L == NULL){return false;}//[1]初始化动态数组的内存空间//注意：因为动态顺序表定义时只定义了一个指针，没有给指针分配空间，这是一个极其危险的野指针//所以我们需要为它分配一片空间，而且这片空间的大小应该由初始化时定义的InitSize来决定L->elem = (ElemType*)malloc(sizeof(ElemType) * InitSize);//sizeof(ElemType)*InitSize):本程序中的ElemType是结构体类型（包含了int 类型的 关键字域），所以这里分配了InitSize个结构体类型的空间//[2]检查内存分配是否成功if (L->elem == NULL){printf("顺序表内存分配失败！");return false;}//[3]初始化表长L->length = 0;//[4]初始化动态顺序表的最大容量//注意这里的最大容量是初始值（即前面定义过的InitSize），后续有需求的时候可以进行扩容L->maxsize = InitSize;return true;
}//6.动态顺序表的元素插入
//可以类比静态顺序表的插入操作
bool SeqListInsert(SSTable* L, int i, KeyType e)//在顺序表的第i个【元素位序】位置插入一个新元素e
{//[1]确保顺序表指针和数据指针不为空if (L == NULL || L->elem == NULL){printf("顺序表指针为空或数据指针为空！\n");return false;}//[2]判断插入操作是否合法//<1>插入位置不合法// （比如一个顺序表长度为8，而插入位置是【元素位序】第0位【即数组下标】[-1]，插入位置是【元素位序】第10位【即数组下标】[9]等）//注意：数组末的下一个元素的位置是可以插入的（即在顺序表的末尾添加一个元素）此时【元素位序】第Length+1位//但是数组末的下下个元素及以后位置不能插入if (i<1 || i>L->length + 1){printf("插入位置不合法！\n");// return false;}//<2>顺序表已经存满了，不能再插入if (L->length >= L->maxsize)//最大容量为可变值maxsize{printf("顺序表已满！\n");return false;}//[3]将新元素插入到正确的位置------区分数组下标[i-1]和元素位序[i]的排列（元素位序比数组下标大1）//<1>将【元素位序】第i位以及第i位之后的所有元素后移一位for (int j = L->length; j >= i; j--){L->elem[j] = L->elem[j - 1];}//现在的j就是数组下标//<2>在【元素位序】第i位【即数组下标】第i-1位插入新元素eL->elem[i-1].key = e;//[4]顺序表长度+1L->length++;//[5]返回true,插入成功return true;}//2.2动态顺序表的输出
bool SeqListPrint(SSTable L)
{//[1]判断是否为空表if (L.length == 0){printf("该顺序表是空表!\n");return false;}//[2]输出顺序表的元素printf("SeqList:\n");for (int i = 0; i < L.length; i++){printf("%d-->", L.elem[i].key);}printf("end\n");return true;
}//顺序表的查找算法：(从最后一个元素开始比较)
//在顺序表L中,查找值为key的数据元素，若成功返回其位置信息，否则返回0；
//注意这里的位置信息就是顺序表数组下标：从1开始（因为我们是从下标1开始存储第一个有效数据的）//1.不带监视哨的顺序查找法
//思路：从后往前比较，直到找到key或比较到最后一个元素
//时间复杂度：O(n)
//空间复杂度：O(1)//方式1：
int Search1(SSTable L, KeyType key)
{for (int i = L.length; i >= 1; i--){if (L.elem[i].key == key){return i;}}return 0;
}//其他方式：（主要包含了边界条件的判断）
//方式2：
int Search2(SSTable L, KeyType key)
{int i;for (i = L.length; L.elem[i].key!=key; i--){if (i <= 0){break;}}if (i > 0){return i;}else{return 0;}}//方式3：
int Search3(SSTable L, KeyType key)
{int i;for (i = L.length; L.elem[i].key != key && i > 0; i--);//这里实际上就是将两个判断条件合并了 一定要注意这里的for循环没有循环体，需要加引号。if (i > 0){return i;}else{return 0;}}//2.改进后带监视哨的顺序查找法
//思路：把待查关键字key存入表头（哨兵，监视哨）从后往前比较，直到找到key或比较到最后一个元素，直接返回i的值
//可以减少查找过程中每一步都要检测是否查找完毕，加快了查找速度int Search4(SSTable L, KeyType key)
{//[1]初始化监视哨L.elem[0].key = key;//[2]顺序查找操作：int i;for ( i = L.length; L.elem[i].key != key; i--);//[3]返回最后的i值：//如果能找到key，那么i就是key的位置，否则i就是0（即监视哨位置的下标）return i;
}//注意：我们将有效数据从数组中下标为1的位置开始存储，即元素位序为2的位置开始存储
int main()
{SSTable L;InitSeqList(&L);//这里直接初始化11个数据，不考虑动态扩容SeqListInsert(&L, 1, -99);//第一个数据，即插入到数组下标为0的位置，是垃圾值-99SeqListInsert(&L, 2, 5);SeqListInsert(&L, 3, 7);SeqListInsert(&L, 4, 19);SeqListInsert(&L, 5, 21);SeqListInsert(&L, 6, 13);SeqListInsert(&L, 7, 56);SeqListInsert(&L, 8, 64);SeqListInsert(&L, 9, 92);SeqListInsert(&L, 10, 88);SeqListInsert(&L, 11, 80);SeqListInsert(&L, 12, 75);SeqListPrint(L);printf("13查找结果：%d\n", Search4(L, 13));printf("60查找结果：%d\n", Search4(L, 60));return 0;
}

在这里插入图片描述

3.2.5顺序查找算法的分析：

  • 效率分析：

如下图，共11个元素，查找失败，比较12次
在这里插入图片描述
则有结论：比较次数与key位置有关

查找第i个元素，需要比较n-i+1次
查找失败，需比较n+1次
在这里插入图片描述
在这里插入图片描述

  • 效率优化方法：
    在这里插入图片描述

3.3线性表的二分查找

本篇前提：

  • 每个元素按非递减有序排列
  • 有效数据从下标为1开始存储

3.3.3二分查找的非递归算法

在这里插入图片描述

算法核心思路：

  • （1）初始化上下界（注意这里从下标1开始存储有效数据）
  • （2）循环查找key值
  • （2.1）更新中点下标
  • 若中点元素等于key，返回中点下标
  • 若中点元素大于key，证明待查找元素在前半区间，缩小上界
  • 若中点元素小于key，证明待查找元素在后半区间，缩小下界
  • 若没有找到返回0
//[0]非递归算法只需要传入  顺序表  和  待查找数据key 这两个参数
int Search1(SSTable L,KeyType key)
{//[1]初始化上下界int low = 1, high = L.length;//[2]循环查找key值while (low<=high)//注意终止条件为low>high{//[2.1]更新中点下标KeyType mid = (low + high) / 2;//[2.2]若中点元素等于key，返回中点下标if (L.elem[mid].key == key){return mid;}//[2.3]若中点元素大于key，证明待查找元素在前半区间，缩小上界else if(L.elem[mid].key > key){high = mid - 1;}//[2.4]若中点元素小于key，证明待查找元素在后半区间，缩小下界else{low = mid + 1;}}//没有找到返回0return 0;
}

3.3.4二分查找的递归算法

核心思路与非递归完全一致，只不过传参时需要传入low,high（递归的前提条件）

算法核心思路：

  • （1）先写递归结束条件
  • （2）更新中点下标
  • （3）递归寻找对应元素
  • 若中点元素等于key，返回中点下标
  • 若中点元素大于key，递归查找前半区间
  • 若中点元素等于key，递归查找后半区间
//2.顺序表的二分查找算法（递归）
//有效数据从下标1开始存储//[0]注意传入  顺序表  和  待查找数据key  起始元素下标 最后一个元素下标 这四个参数（后两个参数是为了递归做准备）
int Search2(SSTable L, KeyType key,int low,int high)
{//[1]递归结束条件if (low > high){return 0;}//[2]更新中点下标KeyType mid = (low + high) / 2;//递归寻找对应元素//[2.1]若中点元素等于key，返回中点下标if (L.elem[mid].key == key){return mid;}//[2.2]若中点元素大于key，递归查找前半区间else if (L.elem[mid].key > key){return Search2(L, key, low, mid - 1);}//[2.3]若中点元素等于key，递归查找后半区间else{return Search2(L, key, mid + 1, high);}
}

3.3.5二分查找的实例分析与相关总结

3.3.5.1实例分析：

以查找21成功为实例：
在这里插入图片描述
在这里插入图片描述
中点值大于key，缩短上半区间
在这里插入图片描述
中间值小于key，缩短下半区间
在这里插入图片描述
找到key值
在这里插入图片描述

3.3.5.2相关总结如下：

以非递减有序排列为实例：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.3.6 两种算法操作一览：

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>//定义动态顺序表初始默认最大容量
#define InitSize 13typedef int KeyType;
//KeyType:是顺序表中每个关键字的类型//1.顺序表的表示：//1.1数据元素类型定义
typedef struct
{KeyType key;//关键字域//除了关键字域以外，还可以定义其他域
}ElemType;//ElemType:是顺序表中的数据类型//1.2顺序表的结构类型定义typedef struct
{ElemType* elem;//顺序表的基地址（动态数组存储）int length;//表长int maxsize;//顺序表的最大容量
}SSTable;//SSTable:用来定义一个顺序表//2.顺序表的一些基本操作：（与之前所学完全一致）
//这里仅涉及初始化，与输出（重点是查找算法）//2.1顺序表的初始化（动态顺序表）
bool InitSeqList(SSTable* L)
{//[0]防止程序潜在异常if (L == NULL){return false;}//[1]初始化动态数组的内存空间//注意：因为动态顺序表定义时只定义了一个指针，没有给指针分配空间，这是一个极其危险的野指针//所以我们需要为它分配一片空间，而且这片空间的大小应该由初始化时定义的InitSize来决定L->elem = (ElemType*)malloc(sizeof(ElemType) * InitSize);//sizeof(ElemType)*InitSize):本程序中的ElemType是结构体类型（包含了int 类型的 关键字域），所以这里分配了InitSize个结构体类型的空间//[2]检查内存分配是否成功if (L->elem == NULL){printf("顺序表内存分配失败！");return false;}//[3]初始化表长L->length = 0;//[4]初始化动态顺序表的最大容量//注意这里的最大容量是初始值（即前面定义过的InitSize），后续有需求的时候可以进行扩容L->maxsize = InitSize;return true;
}//6.动态顺序表的元素插入
//可以类比静态顺序表的插入操作
bool SeqListInsert(SSTable* L, int i, KeyType e)//在顺序表的第i个【元素位序】位置插入一个新元素e
{//[1]确保顺序表指针和数据指针不为空if (L == NULL || L->elem == NULL){printf("顺序表指针为空或数据指针为空！\n");return false;}//[2]判断插入操作是否合法//<1>插入位置不合法// （比如一个顺序表长度为8，而插入位置是【元素位序】第0位【即数组下标】[-1]，插入位置是【元素位序】第10位【即数组下标】[9]等）//注意：数组末的下一个元素的位置是可以插入的（即在顺序表的末尾添加一个元素）此时【元素位序】第Length+1位//但是数组末的下下个元素及以后位置不能插入if (i<1 || i>L->length + 1){printf("插入位置不合法！\n");// return false;}//<2>顺序表已经存满了，不能再插入if (L->length >= L->maxsize)//最大容量为可变值maxsize{printf("顺序表已满！\n");return false;}//[3]将新元素插入到正确的位置------区分数组下标[i-1]和元素位序[i]的排列（元素位序比数组下标大1）//<1>将【元素位序】第i位以及第i位之后的所有元素后移一位for (int j = L->length; j >= i; j--){L->elem[j] = L->elem[j - 1];}//现在的j就是数组下标//<2>在【元素位序】第i位【即数组下标】第i-1位插入新元素eL->elem[i - 1].key = e;//[4]顺序表长度+1L->length++;//[5]返回true,插入成功return true;}//2.2动态顺序表的输出
bool SeqListPrint(SSTable L)
{//[1]判断是否为空表if (L.length == 0){printf("该顺序表是空表!\n");return false;}//[2]输出顺序表的元素printf("SeqList:\n");for (int i = 0; i < L.length; i++){printf("%d-->", L.elem[i].key);}printf("end\n");return true;
}//顺序表的查找算法：
//在顺序表L中,查找值为key的数据元素，若成功返回其位置信息，否则返回0；
//注意这里的位置信息就是顺序表数组下标：从1开始（因为我们是从下标1开始存储第一个有效数据的）//1.顺序表的二分查找算法（非递归）
//有效数据从下标1开始存储//[0]非递归算法只需要传入  顺序表  和  待查找数据key 这两个参数
int Search1(SSTable L,KeyType key)
{//[1]初始化上下界int low = 1, high = L.length;//[2]循环查找key值while (low<=high)//注意终止条件为low>high{//[2.1]更新中点下标KeyType mid = (low + high) / 2;//[2.2]若中点元素等于key，返回中点下标if (L.elem[mid].key == key){return mid;}//[2.3]若中点元素大于key，证明待查找元素在前半区间，缩小上界else if(L.elem[mid].key > key){high = mid - 1;}//[2.4]若中点元素小于key，证明待查找元素在后半区间，缩小下界else{low = mid + 1;}}//没有找到返回0return 0;
}//2.顺序表的二分查找算法（递归）
//有效数据从下标1开始存储//[0]注意传入  顺序表  和  待查找数据key  起始元素下标 最后一个元素下标 这四个参数（后两个参数是为了递归做准备）
int Search2(SSTable L, KeyType key,int low,int high)
{//[1]递归结束条件if (low > high){return 0;}//[2]更新中点下标KeyType mid = (low + high) / 2;//[2.1]若中点元素等于key，返回中点下标if (L.elem[mid].key == key){return mid;}//[2.2]若中点元素大于key，递归查找前半区间else if (L.elem[mid].key > key){return Search2(L, key, low, mid - 1);}//[2.3]若中点元素等于key，递归查找后半区间else{return Search2(L, key, mid + 1, high);}
}//注意：我们将有效数据从数组中下标为1的位置开始存储，即元素位序为2的位置开始存储
//同时需要注意二分查找的前提是：顺序表已排序（非递减有序排列  或者非递增有序排列）
int main()
{SSTable L;InitSeqList(&L);//这里我们直接构造1个非递减有序排列的顺序表//有效数据从顺序表下标为1开始存储SeqListInsert(&L, 1, -99);//第一个数据，即插入到数组下标为0的位置，是垃圾值-99SeqListInsert(&L, 2, 5);SeqListInsert(&L, 3, 13);SeqListInsert(&L, 4, 19);SeqListInsert(&L, 5, 21);SeqListInsert(&L, 6, 37);SeqListInsert(&L, 7, 56);SeqListInsert(&L, 8, 64);SeqListInsert(&L, 9, 75);SeqListInsert(&L, 10, 80);SeqListInsert(&L, 11, 88);SeqListInsert(&L, 12, 92);SeqListPrint(L);printf("21查找结果：%d\n", Search1(L, 21));printf("60查找结果：%d\n", Search2(L, 60,1,L.length));return 0;
}

在这里插入图片描述

3.3.7二分查找算法的分析：

3.3.7.1使用二叉判定树进行分析：

以这11个元素为实例：在这里插入图片描述
我们将每次查找的元素下标放在二叉树中的对应位置
（下半区间的元素放在左子树中，上半区间的元素放在右子树中）

则分析结果如图所示：
在这里插入图片描述
得到结论：二分查找的时间复杂度为O(logn)

3.3.7.2二分查找的平均查找长度：（成功时）

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.4线性表的分块查找（了解）

分块查找-----为索引查找的一种方法，广泛应用于数据库中：

分块查找的特征：

  • 块内无序
  • 块间有序
    在这里插入图片描述
    查找效率与优缺点分析如下：
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

http://www.mrgr.cn/news/44690.html

相关文章：

  • WPF|依赖属性SetCurrentValue方法不会使绑定失效， SetValue方法会使绑定失效？是真的吗？
  • Vue2电商平台(五)、加入购物车，购物车页面
  • 黑马头条（10-1开始学习）
  • 【计算机网络 - 基础问题】每日 3 题（二十九）
  • 数据结构与算法笔记：概念与leetcode练习题
  • 手术器械检测系统源码分享
  • 如何给父母安排体检？
  • Cherno游戏引擎笔记（61~72）
  • jwt认证课件讲解
  • 2014/10/7 408 20题
  • C# 泛型编程基础：自定义泛型类、方法与接口的应用
  • pip丢了怎么办！不用怕，教你用get-pip.py来下载
  • Nacos
  • Vue基础练习|ref
  • 【微服务】springboot 实现动态修改接口返回值
  • Nacos 推送配置到本地的原理与新增、修改的区别详解
  • 大模型基础架构
  • C语言 | 第十一章 | static 日期函数 数学函数
  • 【无人机设计与控制】基于蜣螂优化算法的无人机三维路径规划Matlab程序
  • Codeforces Round 945 (Div. 2) A-C