最大似然估计，存在即合理

一、感性认识

认识的第一步来自感性的认识，先来感性的了解一下最大似然估计。现在，假设有两个学院，物理和外语学院。两个学院都各有特点，物理学院的男生占比大，外语学院女生占比大。如果在一次实验从两个学院中随机的抽取出一个人，结果取出的是男生。现在问你，男生从哪个学院中取出？我们的第一印象就是，此男生最可能从物理学院抽取的，因为物理学院出男生的概率最大，这种估计的想法就是最大似然估计的原理。

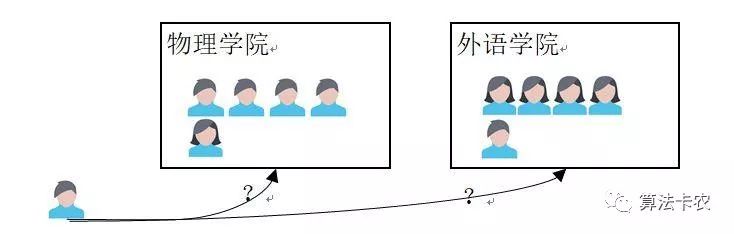
在模型的参数估计中也是一样的，已知某个随机样本满足某种概率分布，即知道样本的描述模型，但是其中具体的参数未知。参数估计就是通过若干次试验并记录样本结果，最后认为出现的样本结果就是模型最真实的表现，即样本结果对于这个模型来说出现的概率最大(存在即合理)，通过极大化这种概率来获得估计的参数，这就是最大似然估计的核心。

最大似然估计是遗传学家以及统计学家罗纳德·费雪在1921年至1922年间开始使用，是频率学派的主张，利用已知的样本结果，反推最有可能导致这样结果的参数值，它与回归模型一样是参数估计的方法之一。在参数估计上，相对于贝叶斯学派，频率主义学派认为参数虽然未知，但确实客观存在的固定值，因此，可通过优化似然函数等准则来确定参数值。

二、最大似然函数

简单起见，我们假设这些观测值都是相同独立的，也就是这些观测值独立分布。由于样本集中的样本都是独立分布，可以只考虑一类样本集D，来估计参数向量 。记已知的样本集为：

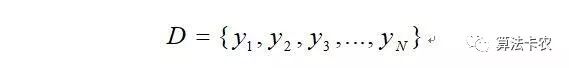
我们将样本的联合概率密度函数称为相对于θ的似然函数。

如果θ'是参数空间中能使似然函数l(θ)最大的θ值，那么θ'就是θ的最大似然估计量，也就是我们要求的估计参数向量。它是样本集的函数，记作：

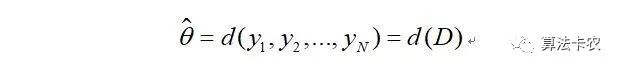
称作最大似然函数估计值。

三、求解最大似然函数

目标是求使得出现该样本概率最大的 值(arg max解释为后面表达式中取最大值时参数的取值，毕竟我们是参数估计)。

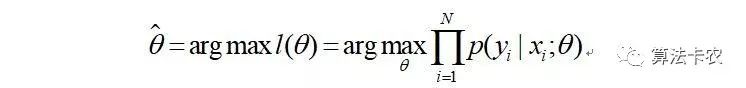
这里运用了一点技巧，定义了一个对数似然函数，将连乘转为求和从而方便计算。

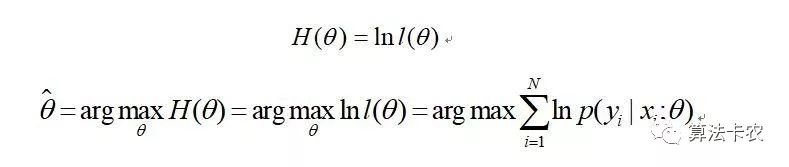
接下来就好处理了，对 求偏导获得参数。

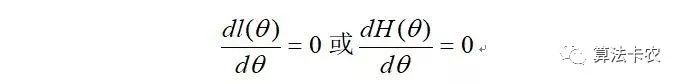
最大似然估计只是一种粗略的数学期望，要知道它的误差大小还需要做区间估计。最大似然估计在样本趋于无穷大时，就收敛率而言是最好的渐近估计，最大似然估计通常是机器学习中的首选估计方法。

四、最大似然函数与最小二乘法

二者的都是参数估计的方法，都把参数估计问题变成了最优化问题。最小二乘法是一个凸优化问题，最大似然估计却不一定是。另外，样本误差服从高斯分布的情况下，最小二乘法等价于极大似然估计。

假设有:

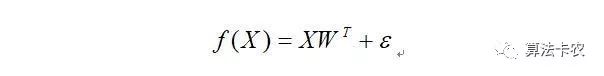
样本误差服从高斯分布的情况下有：

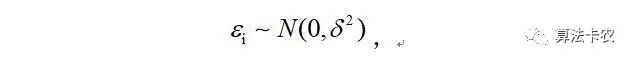
两边都加一个yi，那么，则有：

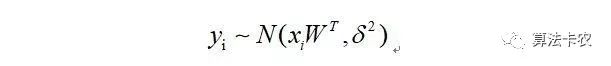
那么：

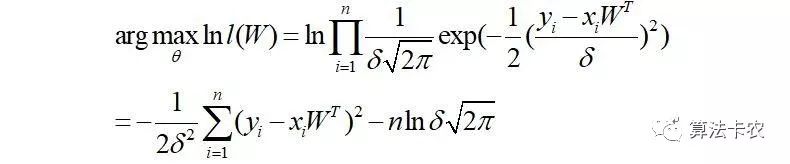
最终化简为：

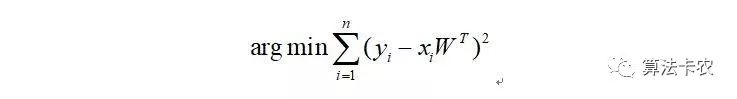
这正是最小二乘法的目标函数。

将会将《算法成长之路》写成一个系列，喜欢的加关注，精彩内容