当前位置：首页 > news >正文

2024年研赛-华为杯数模竞赛C题论文首发+论文讲解+代码分享

news 2024/11/13 22:03:20

2024年华为杯-研赛分享资料（论文分享+部分代码）（已更新部分代码）：链接：https://pan.baidu.com/s/1HGIYjV3lqzUc_3H0vg5H8w 提取码：sxjm

题目： _基于数据驱动下磁性元件的磁芯损耗建模

摘要：

随着国民经济发展和社会进步，基于电力电子技术的电能变换（得到迅速发展，尤其是新能源和信息通讯领域。本文将基于数据驱动下磁性元件的磁芯损耗建模。

针对问题一，基于实验数据，提取反映磁通密度分布和波形特征的变量，进而对三种波形（正弦波、三角波、梯形波）进行分类。通过提取磁通密度随时间变化的特征量，建立了一个特征提取机制。随后，采用随机森林分类器作为模型，对这些特征进行分类建模。训练集中的数据用于拟合分类器，而测试集数据用于验证模型的效果。模型成功对三种波形进行了分类，并得到了准确的分类结果。

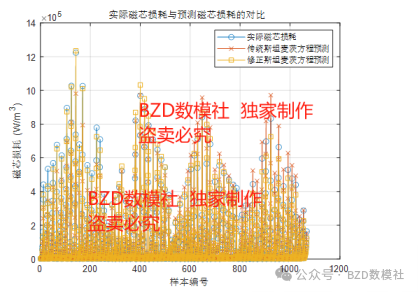
针对问题二，基于实验数据，修正斯坦麦茨方程，增加温度修正项，以适应不同温度条件下的损耗预测。使用实验数据，分别拟合传统斯坦麦茨方程和修正后的方程，利用最小二乘法（lsqcurvefit）对参数 k1、a、b和温度修正系数c 进行拟合。修正后的斯坦麦茨方程能够更准确地预测不同温度下的磁芯损耗。对比传统斯坦麦茨方程与修正模型，后者的预测误差显著降低，最终模型的均方误差（MSE）也得到了显著改善。

针对问题三，分析这些因素对损耗的独立及协同影响，并找到使磁芯损耗最小的最优条件。采用多元回归模型分析材料、温度、励磁波形和频率对磁芯损耗的影响，模型考虑了独立效应以及两两因素之间的交互作用。通过对不同组合的实验数据进行分析，计算出每种材料和波形在不同温度下的平均损耗。同时，利用可视化工具进一步分析这些因素的交互作用。通过回归模型的预测与分析，找到了使磁芯损耗最小的最优条件：在材料4、温度为90℃、频率为50010Hz、正弦波形下，磁芯损耗最小值。

一、问题重述

1.1 问题背景

1.2 问题回顾

二、问题分析

2.1 数据分析

2.2 问题一分析

2.3 问题二分析

2.4 问题三分析

2.5 问题四分析

2.6 问题五分析

三、模型假设

四、符号说明

五、模型的建立与求解

5.1 数据预处理

5.1.1 数据清洗

5.1.2 数据转码

5.1.3 数据描述性分析

5.2 问题一模型的建立与求解

5.2.1 分类模型的建立

5.2.2 分类结果

5.3 问题二模型的建立与求解

5.3.1 修正模型的建立

5.3.1 修正模型求解

5.4 问题三模型的建立与求解

5.4.1 回归模型的建立与求解

5.4.2 交互模型的建立与求解

5.4.3 极值的求解

5.5 问题四模型的建立与求解

5.5.1 数据处理

5.5.2 预测模型的选择

5.5.3 加权预测模型

5.5.4 预测结果的比对

5.6 问题五模型的建立与求解

5.6.1 优化模型的建立

5.6.2 优化模型的求解

六、模型总结

6.1 模型优点

6.2 模型缺点

6.3 模型推广

七、参考文献

八、附录

一、模型的建立与求解

5.1 数据预处理

5.1.1 数据清洗

利用matlab的find函数对数据集的缺失值进行查找，得到题目给出数据并没有存在缺失值。对于异常值的判定，题目给出的数据，例如题目中存在极端异常的数据，例如无论是存在极端数据，需对该极端数据进行处理，首先对数据进行正态分布的检验。为了更加直观的观察异常数据，利用matlab绘制了三种指标的数据柱状图如下所示

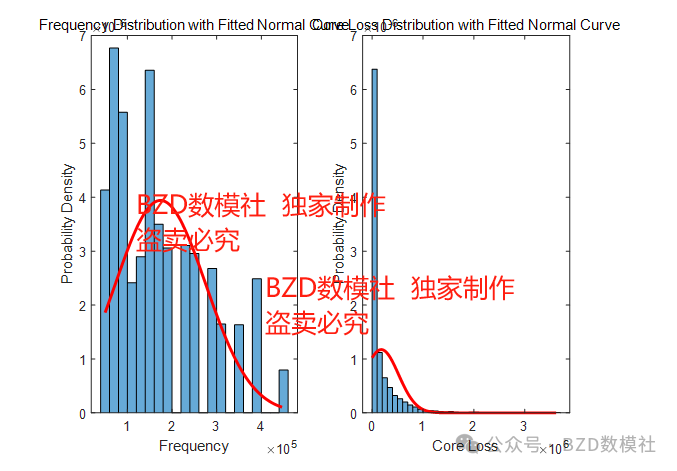
对数据进行箱型图检验，使用MATLAB中boxplot 函数来生成箱型图并标识异常值。箱型图是一种用于显示一组数据分布的图表，其中“异常值”通常被定义为小于 Q1 1.5IQR 或大于 Q3 + 1.5IQR 的值（其中 Q1 是第一四分位数，Q3 是第三四分位数，IQR 是四分位间距）。

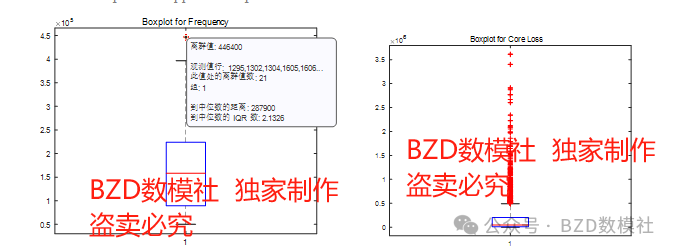
对于得到的异常值，根据实际情况进行人为判定。

5.1.2 数据转码

别型变量的编码：如励磁波形（正弦波、三角波、梯形波）和磁芯材料（材料1、材料2、材料3、材料4），这些类别特征在建模时不能直接用于数值计算，因此需要进行编码。

名称	转码后结果	名称	转码后结果
正弦波	1	材料1	1
三角波	2	材料2	2
梯形波	3	材料3	3
		材料4	4

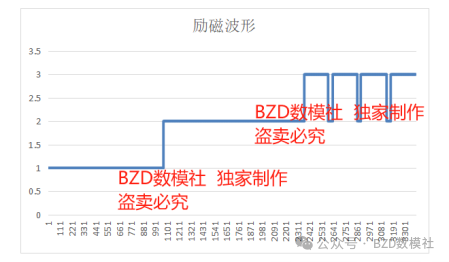
为了更加直观地展示转码后结果，绘制可视化结果如下所示

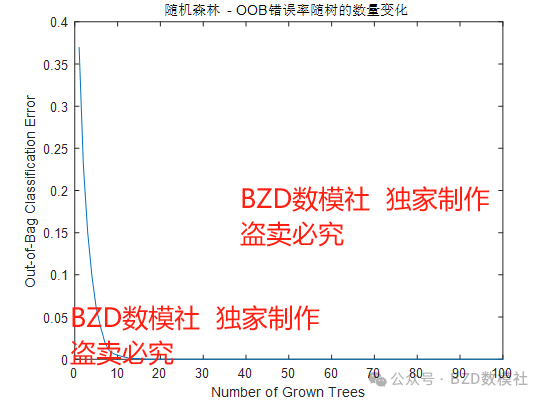
袋外错误率（Out-of-Bag Error）曲线展示了随着随机森林中树的数量增加，模型的分类错误率是如何变化的。横轴代表决策树的数量，纵轴代表袋外错误率。可以看到：

在最开始时，随着树的数量增加，错误率迅速下降。

当树的数量达到20棵后，错误率趋于平稳并接近零，表明模型几乎没有错误。

袋外错误率的下降趋势表明，模型在增加更多树的初期阶段能够显著提高性能，但在树的数量达到一定程度后，更多的树对模型性能的提升已经不再明显。

结论：随机森林在包含约20棵树时，袋外错误率已接近零，说明此时模型的泛化能力已经非常好，继续增加树的数量对提升模型性能的作用有限。
4. 特征重要性

随机森林具有自动计算特征重要性的能力。通过对特征的随机扰动来观察模型性能的变化，能够得出每个特征在分类中的贡献度。具体过程如下:

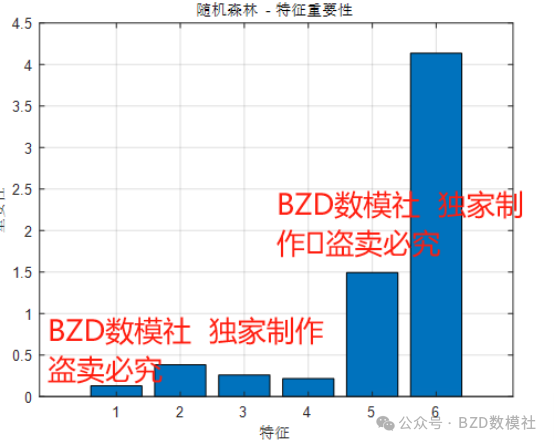
结论：决策树展示了模型分类时的逻辑，树的分裂主要依赖特征5和特征6。树的深度较浅，表明模型的复杂度较低，分类规则简单。

表1：问题一结果

序号	类型	序号	类型	序号	类型	序号	类型
1	三角波	21	正弦波'	41	正弦波'	61	正弦波'
2	三角波	22	正弦波'	42	三角波'	62	正弦波'
3	三角波	23	正弦波'	43	正弦波'	63	正弦波'
4	三角波	24	正弦波'	44	正弦波'	64	正弦波'
5	三角波	25	正弦波'	45	正弦波'	65	正弦波'
6	梯形波	26	三角波'	46	梯形波'	66	正弦波'
7	梯形波	27	三角波'	47	梯形波'	67	正弦波'
8	梯形波	28	三角波'	48	梯形波'	68	正弦波'
9	梯形波	29	三角波'	49	梯形波'	69	正弦波'
10	梯形波	30	三角波'	50	梯形波'	70	正弦波'
11	正弦波	31	梯形波'	51	三角波'	71	正弦波'
12	正弦波	32	梯形波'	52	三角波'	72	三角波'
13	正弦波	33	梯形波'	53	三角波'	73	三角波'
14	正弦波	34	梯形波'	54	三角波'	74	正弦波'
15	正弦波	35	梯形波'	55	三角波'	75	正弦波'
16	三角波	36	正弦波'	56	三角波'	76	梯形波'
17	三角波	37	正弦波'	57	三角波'	77	梯形波'
18	三角波	38	正弦波'	58	三角波'	78	梯形波'
19	三角波	39	正弦波'	59	三角波'	79	梯形波'
20	三角波	40	正弦波'	60	三角波'	80	梯形波'