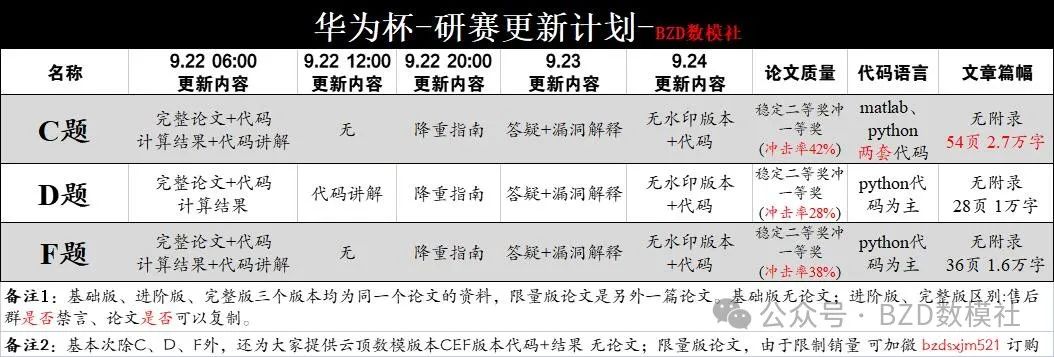
2024年研赛 C、D、F三题论文首发+部分代码分享
本届研赛助攻题目 C D F三题论文均已经全部完成。后更新计划 如图所示。
免费给大家分享 三个问题的论文+部分代码
2024年华为杯-研赛分享资料(论文+部分代码)(已更新部分代码):
链接:https://pan.baidu.com/s/1HGIYjV3lqzUc_3H0vg5H8w
提取码:sxjm



题 目: _基于数据驱动下磁性元件的磁芯损耗建模
摘 要:
随着国民经济发展和社会进步,基于电力电子技术的电能变换(得到迅速发展,尤其是新能源和信息通讯领域。本文将基于数据驱动下磁性元件的磁芯损耗建模。
针对问题一,基于实验数据,提取反映磁通密度分布和波形特征的变量,进而对三种波形(正弦波、三角波、梯形波)进行分类。通过提取磁通密度随时间变化的特征量,建立了一个特征提取机制。随后,采用随机森林分类器作为模型,对这些特征进行分类建模。训练集中的数据用于拟合分类器,而测试集数据用于验证模型的效果。模型成功对三种波形进行了分类,并得到了准确的分类结果。
针对问题二,基于实验数据,修正斯坦麦茨方程,增加温度修正项,以适应不同温度条件下的损耗预测。使用实验数据,分别拟合传统斯坦麦茨方程和修正后的方程,利用最小二乘法(lsqcurvefit)对参数 k1、a、b和温度修正系数c 进行拟合。修正后的斯坦麦茨方程能够更准确地预测不同温度下的磁芯损耗。对比传统斯坦麦茨方程与修正模型,后者的预测误差显著降低,最终模型的均方误差(MSE)也得到了显著改善。
针对问题三,分析这些因素对损耗的独立及协同影响,并找到使磁芯损耗最小的最优条件。采用多元回归模型分析材料、温度、励磁波形和频率对磁芯损耗的影响,模型考虑了独立效应以及两两因素之间的交互作用。通过对不同组合的实验数据进行分析,计算出每种材料和波形在不同温度下的平均损耗。同时,利用可视化工具进一步分析这些因素的交互作用。通过回归模型的预测与分析,找到了使磁芯损耗最小的最优条件:在材料4、温度为90℃、频率为50010Hz、正弦波形下,磁芯损耗最小值。
针对问题四,在磁芯损耗预测的研究中,本文结合多种机器学习模型,包括随机森林、线性回归、梯度提升树、人工神经网络、K-最近邻回归、决策树、贝叶斯回归以及 Lasso 回归,构建了多
题 目: 大数据驱动的地理综合问题
摘 要:
地理系统是自然、人文多要素综合作用的复杂巨系统,地理学家常用地理综合的方式对地理系统进行主导特征的表达,本文利用大数据的手段对地理系统进行综合,探索全球气候变化下中国地理环境的演化。
针对问题一,本文首先对数据进行清洗,替换一些取值较大或较小的特殊值,并利用准则确定一些离群点,然后使用数字、图表等方式,对原始数据进行定量总结、概括,得出了一些降水量、土地利用/土地覆被面积两个变量的在1990至2020年间中国范围内的时空演化特征。
针对问题二,首先利用逻辑回归模型量化地形-气候相互作用在极端天气形成过程中的作用,再用格兰杰因果检验和斯皮尔曼相关系数加以检验,确定它们之间的相互作用,验证了本文模型建立的有效性,为后文预测的准确性奠定基础。
针对问题三,首先对题目中提到的自变量进行量化,建立逻辑回归模型,再利用移动平均线模型和LSTM神经网络进行预测,将预测的数据代入前面建立的逻辑回归模型进行降水量的预测,利用不同的成灾临界值可确定不同的防范政策。若需要推广至多分类问题,为不同地区制定不同政策,也即对全国所有城市分类出应对暴雨灾害能力最为脆弱、较为脆弱、一般、不脆弱等类的话,只需将本文中的成灾临界值
X射线脉冲星光子到达时间建模
摘要
脉冲星是一类高速自转的中子星,其自转形成规律性脉冲信号,类似于“宇宙中的灯塔”,因此被认为是极为精确的时钟。X射线脉冲星导航利用脉冲星信号为航天器提供时间和空间参考。通过比较脉冲信号到达航天器和太阳系质心的时间差,能够实现航天器的精确定位。为了准确计算该时间差,需要考虑卫星的轨道运动、脉冲星光子传播过程中的几何时延、Shapiro时延、引力红移效应及相对论效应等多种复杂因素。
2016年,我国发射的XPNAV-1卫星观测了蟹状星云脉冲星(PSR B0531+21)的X射线信号。该任务要求通过光子到达时间模拟和折叠,得到脉冲星的精确计时轮廓,为脉冲星导航系统的发展提供重要数据支持。
针对问题1,首先,利用给定的轨道根数 (偏心率 、角动量 、轨道倾角 、升交点赤经 、近地点幅角 、和真近点角 ),通过公式计算卫星在轨道平面内的径向距离 以及径向速度 和切向速度 。接着,通过旋转矩阵将卫星的二维轨道位置和速度从轨道平面转换到地心天球参考系 (GCRS) 中的三维位置和速度。最终,计算出卫星在特定时刻的三维位置 和速度分量 ,验证卫星的三维位置和速度计算是准确的,且与轨道参数吻合。
针对问题2,建立一个脉冲星光子到达卫星与太阳系质心之间的几何传播时延模型。针对问题2,首先利用脉冲星辐射平行光的假设,忽略太阳系天体的自转和扁率,简化光子的传播路径问题。其次,光子到达卫星的时刻为MJD 57062.0(TT时间尺度),我们需要将卫星在地心天球参考系(GCRS)中的坐标转换为太阳系质心参考系(SSB)。通过DE系列历表和卫星的GCRS坐标,
