算法工程师面试常考手撕题

最近这一两周看到不少互联网公司都已经开始秋招提前批了。

不同以往的是，当前职场环境已不再是那个双向奔赴时代了。求职者在变多，HC 在变少，岗位要求还更高了。

最近，我们又陆续整理了很多大厂的面试题，帮助一些球友解惑答疑，分享技术面试中的那些弯弯绕绕。

• 《大模型面试宝典》(2024版) 正式发布！
• 持续火爆！！！《AIGC 面试宝典》已圈粉无数！

喜欢本文记得收藏、关注、点赞。更多实战和面试交流，文末加入我们

技术交流

---

算法工程师面试常考手撕题

• 注意力（Attention）篇

  • 手撕单头注意力机制（ScaledDotProductAttention）函数

  • 手撕多头注意力（MultiHeadAttention）

  • 手撕自注意力机制函数（SelfAttention）

  • GPT2 解码中的KV Cache

  • 手撕 MQA 算法

• 基础机器学习算法篇

  • 手撕 numpy写线性回归的随机梯度下降（stochastic gradient descent，SGD）

  • 手撕 k-means 算法

  • 手撕 Layer Normalization 算法

  • 手撕 Batch Normalization 算法

• 解码算法篇

  • 手撕 贪心搜索 （greedy search）

  • 手撕 集束搜索 beamsearch 算法

  • 手撕 温度参数采样（Temperature Sampling）算法

  • 手撕 Top-K Sampling算法

  • 手撕 Top-P (Nucleus) Sampling 算法

• 神经网络篇

  • 手撕反向传播(backward propagation，BP)法

  • 手撕 卷积神经网络(CNN)法

  • 手撕 循环神经网络(RNN)法

  • 手撕 LSTM法

  • 手撕 二维卷积 算法

• 位置编码篇

  • 手撕 绝对位置编码 算法

  • 手撕 可学习位置编码 算法

  • 手撕 相对位置编码 算法

  • 手撕 rope 算法

• 面试题汇总

注意力（Attention）篇

手撕单头注意力机制（ScaledDotProductAttention）函数

输入是query和 key-value，注意力机制首先计算query与每个key的关联性（compatibility），每个关联性作为每个value的权重（weight），各个权重与value的乘积相加得到输出。

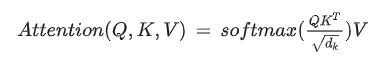
class ScaledDotProductAttention(nn.Module):""" Scaled Dot-Product Attention """def __init__(self, scale):super().__init__()self.scale = scaleself.softmax = nn.Softmax(dim=2)def forward(self, q, k, v, mask=None):u = torch.bmm(q, k.transpose(1, 2)) # 1.Matmulu = u / self.scale # 2.Scaleif mask is not None:u = u.masked_fill(mask, -np.inf) # 3.Maskattn = self.softmax(u) # 4.Softmaxoutput = torch.bmm(attn, v) # 5.Outputreturn attn, outputif __name__ == "__main__":n_q, n_k, n_v = 2, 4, 4d_q, d_k, d_v = 128, 128, 64q = torch.randn(batch, n_q, d_q)k = torch.randn(batch, n_k, d_k)v = torch.randn(batch, n_v, d_v)mask = torch.zeros(batch, n_q, n_k).bool()attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))attn, output = attention(q, k, v, mask=mask)print(attn)print(output)

手撕多头注意力（MultiHeadAttention）

class MultiHeadAttention(nn.Module):""" Multi-Head Attention """def __init__(self, n_head, d_k_, d_v_, d_k, d_v, d_o):super().__init__()self.n_head = n_headself.d_k = d_kself.d_v = d_vself.fc_q = nn.Linear(d_k_, n_head * d_k)self.fc_k = nn.Linear(d_k_, n_head * d_k)self.fc_v = nn.Linear(d_v_, n_head * d_v)self.attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))self.fc_o = nn.Linear(n_head * d_v, d_o)def forward(self, q, k, v, mask=None):n_head, d_q, d_k, d_v = self.n_head, self.d_k, self.d_k, self.d_vbatch, n_q, d_q_ = q.size()batch, n_k, d_k_ = k.size()batch, n_v, d_v_ = v.size()q = self.fc_q(q) # 1.单头变多头k = self.fc_k(k)v = self.fc_v(v)q = q.view(batch, n_q, n_head, d_q).permute(2, 0, 1, 3).contiguous().view(-1, n_q, d_q)k = k.view(batch, n_k, n_head, d_k).permute(2, 0, 1, 3).contiguous().view(-1, n_k, d_k)v = v.view(batch, n_v, n_head, d_v).permute(2, 0, 1, 3).contiguous().view(-1, n_v, d_v)if mask is not None:mask = mask.repeat(n_head, 1, 1)attn, output = self.attention(q, k, v, mask=mask) # 2.当成单头注意力求输出output = output.view(n_head, batch, n_q, d_v).permute(1, 2, 0, 3).contiguous().view(batch, n_q, -1) # 3.Concatoutput = self.fc_o(output) # 4.仿射变换得到最终输出return attn, outputif __name__ == "__main__":n_q, n_k, n_v = 2, 4, 4d_q_, d_k_, d_v_ = 128, 128, 64q = torch.randn(batch, n_q, d_q_)k = torch.randn(batch, n_k, d_k_)v = torch.randn(batch, n_v, d_v_)    mask = torch.zeros(batch, n_q, n_k).bool()mha = MultiHeadAttention(n_head=8, d_k_=128, d_v_=64, d_k=256, d_v=128, d_o=128)attn, output = mha(q, k, v, mask=mask)print(attn.size())print(output.size())

手撕自注意力机制函数（SelfAttention）

Self-Attention。和Attention类似，他们都是一种注意力机制。不同的是Attention是source对target，输入的source和输出的target内容不同。例如英译中，输入英文，输出中文。而Self-Attention是source对source，是source内部元素之间或者target内部元素之间发生的Attention机制，也可以理解为Target=Source这种特殊情况下的注意力机制。

class SelfAttention(nn.Module):""" Self-Attention """def __init__(self, n_head, d_k, d_v, d_x, d_o):self.wq = nn.Parameter(torch.Tensor(d_x, d_k))self.wk = nn.Parameter(torch.Tensor(d_x, d_k))self.wv = nn.Parameter(torch.Tensor(d_x, d_v))self.mha = MultiHeadAttention(n_head=n_head, d_k_=d_k, d_v_=d_v, d_k=d_k, d_v=d_v, d_o=d_o)self.init_parameters()def init_parameters(self):for param in self.parameters():stdv = 1. / np.power(param.size(-1), 0.5)param.data.uniform_(-stdv, stdv)def forward(self, x, mask=None):q = torch.matmul(x, self.wq)   k = torch.matmul(x, self.wk)v = torch.matmul(x, self.wv)attn, output = self.mha(q, k, v, mask=mask)return attn, outputif __name__ == "__main__":n_x = 4d_x = 80x = torch.randn(batch, n_x, d_x)mask = torch.zeros(batch, n_x, n_x).bool()selfattn = SelfAttention(n_head=8, d_k=128, d_v=64, d_x=80, d_o=80)attn, output = selfattn(x, mask=mask)print(attn.size())print(output.size())

GPT2 解码中的KV Cache

无论是encoder-decoder结构，还是现在我们最接近AGI的decoder-only的LLM，解码生成时都是自回归auto-regressive的方式。

也就是，解码的时候，先根据当前输入 ，生成下一个 ，然后把新生成的 拼接在 后面，获得新的输入 ，再用 生成 ，依此迭代，直到生成结束。

我们可以注意到，下一个step的输入其实包含了上一个step的内容，而且只在最后面多了一点点（一个token）。那么下一个step的计算应该也包含了上一个step的计算。

但是模型在推理的时候可不管这些，无论你是不是只要最后一个字的输出，它都把所有输入计算一遍，给出所有输出结果。

也就是说中间有很多我们用不到的计算，这样就造成了浪费。

而且随着生成的结果越来越多，输入的长度也越来越长，上面这个例子里，输入长度就从step0的10个，每步增长1，直到step5的15个。如果输入的instruction是让模型写作文，那可能就有800个step。这个情况下，step0被算了800次，step1被算了799次…这样浪费的计算资源确实不容忽视。

有没有什么办法可以重复利用上一个step里已经计算过的结果，减少浪费呢？

答案就是KV Cache，利用一个缓存，把需要重复利用的中间计算结果存下来，减少重复计算。

而 k 和 v 就是我要缓存的对象。

因为第l层的 o0、o1、o2本来会经过FNN层之后进到 l十1 层，再经过新的投影变换，成为 l + 1 层的 k、υ 值，但是l十 1 层的 k、

这样就节省了attention和FFN的很多重复计算。

transformers中，生成的时候传入use_cache=True就会开启KV Cache。

也可以简单看下GPT2中的实现，中文注释的部分就是使用缓存结果和更新缓存结果

Class GPT2Attention(nn.Module):......def forward(self,hidden_states: Optional[Tuple[torch.FloatTensor]],layer_past: Optional[Tuple[torch.Tensor]] = None,attention_mask: Optional[torch.FloatTensor] = None,head_mask: Optional[torch.FloatTensor] = None,encoder_hidden_states: Optional[torch.Tensor] = None,encoder_attention_mask: Optional[torch.FloatTensor] = None,use_cache: Optional[bool] = False,output_attentions: Optional[bool] = False,) -> Tuple[Union[torch.Tensor, Tuple[torch.Tensor]], ...]:if encoder_hidden_states is not None:if not hasattr(self, "q_attn"):raise ValueError("If class is used as cross attention, the weights `q_attn` have to be defined. ""Please make sure to instantiate class with `GPT2Attention(..., is_cross_attention=True)`.")query = self.q_attn(hidden_states)key, value = self.c_attn(encoder_hidden_states).split(self.split_size, dim=2)attention_mask = encoder_attention_maskelse:query, key, value = self.c_attn(hidden_states).split(self.split_size, dim=2)query = self._split_heads(query, self.num_heads, self.head_dim)key = self._split_heads(key, self.num_heads, self.head_dim)value = self._split_heads(value, self.num_heads, self.head_dim)# 过去所存的值if layer_past is not None:past_key, past_value = layer_pastkey = torch.cat((past_key, key), dim=-2)  # 把当前新的key加入value = torch.cat((past_value, value), dim=-2)  # 把当前新的value加入if use_cache is True:present = (key, value)  # 输出用于保存else:present = Noneif self.reorder_and_upcast_attn:attn_output, attn_weights = self._upcast_and_reordered_attn(query, key, value, attention_mask, head_mask)else:attn_output, attn_weights = self._attn(query, key, value, attention_mask, head_mask)attn_output = self._merge_heads(attn_output, self.num_heads, self.head_dim)attn_output = self.c_proj(attn_output)attn_output = self.resid_dropout(attn_output)outputs = (attn_output, present)if output_attentions:outputs += (attn_weights,)return outputs  # a, present, (attentions)

总的来说，KV Cache是以空间换时间的做法，通过使用快速的缓存存取，减少了重复计算。（注意，只有decoder结构的模型可用，因为有mask attention的存在，使得前面的token可以不用关注后面的token）

手撕 MQA 算法

MQA 让所有的头之间 共享 同一份 Key 和 Value 矩阵，每个头只单独保留了一份 Query 参数，从而大大减少 Key 和 Value 矩阵的参数量。

class MultiQueryAttention(nn.Module):"""Multi-Query self attention.Using torch or triton attention implemetation enables user to also useadditive bias."""def __init__(self,d_model: int,n_heads: int,attn_impl: str = 'triton',clip_qkv: Optional[float] = None,qk_ln: bool = False,softmax_scale: Optional[float] = None,attn_pdrop: float = 0.0,low_precision_layernorm: bool = False,verbose: int = 0,device: Optional[str] = None,):super().__init__()self.attn_impl = attn_implself.clip_qkv = clip_qkvself.qk_ln = qk_lnself.d_model = d_modelself.n_heads = n_headsself.head_dim = d_model // n_headsself.softmax_scale = softmax_scaleif self.softmax_scale is None:self.softmax_scale = 1 / math.sqrt(self.head_dim)self.attn_dropout_p = attn_pdropself.Wqkv = nn.Linear(d_model,d_model + 2 * self.head_dim,device=device,)fuse_splits = (d_model, d_model + self.head_dim)self.Wqkv._fused = (0, fuse_splits)  # type: ignoreself.attn_fn = scaled_multihead_dot_product_attentionself.out_proj = nn.Linear(self.d_model, self.d_model, device=device)self.out_proj._is_residual = True  # type: ignoredef forward(self,x,past_key_value=None,attn_bias=None,attention_mask=None,is_causal=True,needs_weights=False,):qkv = self.Wqkv(x)                                      # (1, 512, 960)if self.clip_qkv:qkv.clamp_(min=-self.clip_qkv, max=self.clip_qkv)query, key, value = qkv.split(                                  # query -> (1, 512, 768)[self.d_model, self.head_dim, self.head_dim],               # key   -> (1, 512, 96)dim=2                                                       # value -> (1, 512, 96))key_padding_mask = attention_maskif self.qk_ln:# Applying layernorm to qkdtype = query.dtypequery = self.q_ln(query).to(dtype)key = self.k_ln(key).to(dtype)context, attn_weights, past_key_value = self.attn_fn(query,key,value,self.n_heads,past_key_value=past_key_value,softmax_scale=self.softmax_scale,attn_bias=attn_bias,key_padding_mask=key_padding_mask,is_causal=is_causal,dropout_p=self.attn_dropout_p,training=self.training,needs_weights=needs_weights,multiquery=True,)return self.out_proj(context), attn_weights, past_key_value

基础机器学习算法篇

手撕 numpy写线性回归的随机梯度下降（stochastic gradient descent，SGD）

在每次更新时用1个样本，可以看到多了随机两个字，随机也就是说我们用样本中的一个例子来近似我所有的样本，来调整θ，因而随机梯度下降是会带来一定的问题，因为计算得到的并不是准确的一个梯度，对于最优化问题，凸问题，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

# 数据加载
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_splitX, Y = fetch_california_housing(return_X_y=True)
X.shape, Y.shape  # (20640, 8), (20640, )# 数据预处理
ones = np.ones(shape=(X.shape[0], 1))
X = np.hstack([X, ones])
validate_size = 0.2
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=validate_size, shuffle=True)# batch 函数
def get_batch(batchsize: int, X: np.ndarray, Y: np.ndarray):assert 0 == X.shape[0]%batchsize, f'{X.shape[0]}%{batchsize} != 0'batchnum = X.shape[0]//batchsizeX_new = X.reshape((batchnum, batchsize, X.shape[1]))Y_new = Y.reshape((batchnum, batchsize, ))for i in range(batchnum):yield X_new[i, :, :], Y_new[i, :]# 损失函数
def mse(X: np.ndarray, Y: np.ndarray, W: np.ndarray):return 0.5 * np.mean(np.square(X@W-Y))def diff_mse(X: np.ndarray, Y: np.ndarray, W: np.ndarray):return X.T@(X@W-Y) / X.shape[0]# 模型训练
lr = 0.001          # 学习率
num_epochs = 1000   # 训练周期
batch_size = 64     # |每个batch包含的样本数
validate_every = 4  # 多少个周期进行一次检验
def train(num_epochs: int, batch_size: int, validate_every: int, W0: np.ndarray, X_train: np.ndarray, Y_train: np.ndarray, X_test: np.ndarray, Y_test: np.ndarray):loop = tqdm(range(num_epochs))loss_train = []loss_validate = []W = W0# 遍历epochfor epoch in loop:loss_train_epoch = 0# 遍历batchfor x_batch, y_batch in get_batch(64, X_train, Y_train):loss_batch = mse(X=x_batch, Y=y_batch, W=W)loss_train_epoch += loss_batch*x_batch.shape[0]/X_train.shape[0]grad = diff_mse(X=x_batch, Y=y_batch, W=W)W = W - lr*gradloss_train.append(loss_train_epoch)loop.set_description(f'Epoch: {epoch}, loss: {loss_train_epoch}')if 0 == epoch%validate_every:loss_validate_epoch = mse(X=X_test, Y=Y_test, W=W)loss_validate.append(loss_validate_epoch)print('============Validate=============')print(f'Epoch: {epoch}, train loss: {loss_train_epoch}, val loss: {loss_validate_epoch}')print('================================')plot_loss(np.array(loss_train), np.array(loss_validate), validate_every)# 程序运行
W0 = np.random.random(size=(X.shape[1], ))  # 初始权重
train(num_epochs=num_epochs, batch_size=batch_size, validate_every=validate_every, W0=W0, X_train=X_train, Y_train=Y_train, X_test=X_test, Y_test=Y_test)