CF 231 E Cactus 题解（仙人掌图上找环）

codeforces 提交记录

题意

有一个点仙人掌图（每个点都只属于至多一个简单环），给出 $k$ 个询问，问点 $x$ 到点 $y$ 有多少条简单路径（经过的边不能重复，点可以）。

思路

一看这个样例输出，就感觉有猫腻，肯定和 $2$ 有关。我们画出一个仙人掌图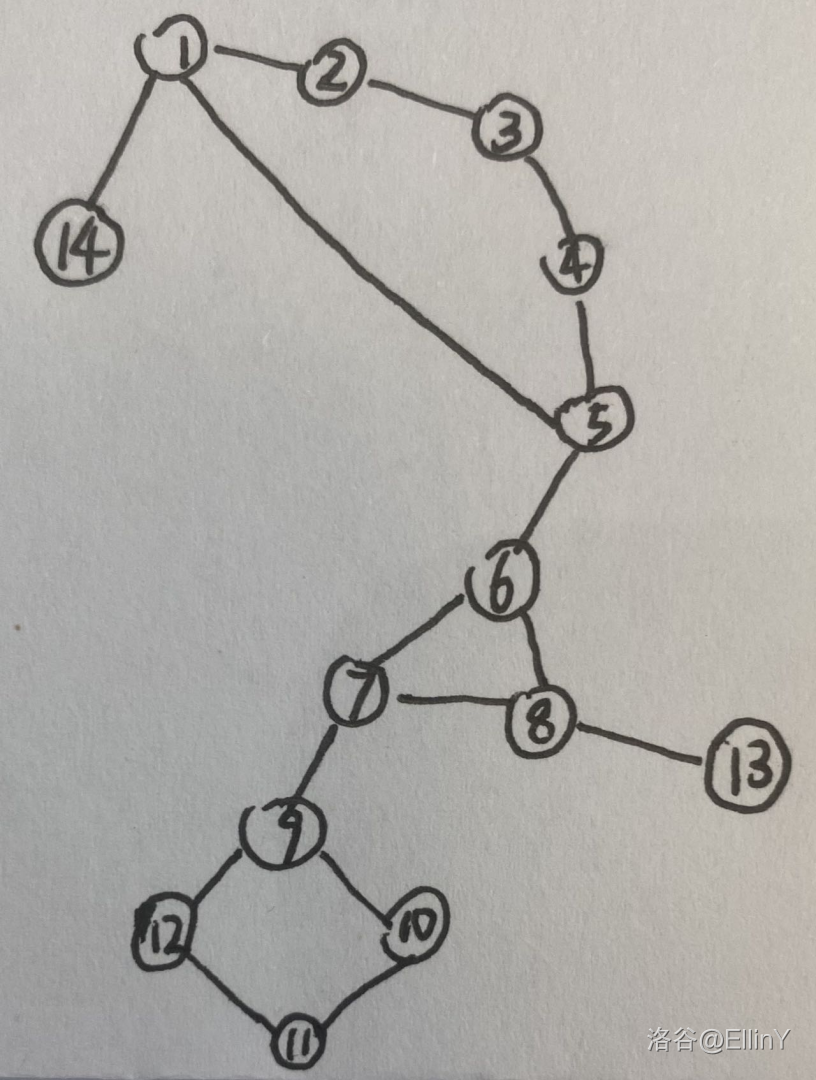：图中有三个简单环：1,2,3,4,5；6,7,8；9,10,11,12。如果问点 3 到点 8 的路径，有 4 条：3,4,5,6,8；3,2,1,5,6,8；3,4,5,6,7,8；3,2,1,5,6,7,8。发现这个路径可以分为三段：第一段在第一个环里从 3 走到 5，有两种走法；第二段从 5 走到 6，进入第二个环；第三段在第二个环里从 6 走到 8。那如果是问 3 到 6 呢？是不是没有第三段了？简单路径只是边不能重复，所以从 6 走到 6 有两种走法，绕一圈（6，7，8，6）或者直接停在 6。走过的边的集合不同则路径不同，所以顺时针绕和逆时针绕没有区别。从 5 走到 6 也是 4 种。可以再模拟一下从 3 走到 12，发现是 8 种。得出结论：经过了几个环，就是 2 的几次方，这里的环包括起点和终点所在的环。

实现

由于这张图是一个仙人掌，所以当把每个环都缩成一个点的时候，图就会变成一棵树。我们先用 dfs 找到所有环，在同一个环里的用 $b_i$ 标记为相同的数值（数值从 $n+1$ 开始，方便区分原来的点和缩点得到的点）。重新建图，对树进行前缀和，用 $su{m}_i$ 表示从根节点（$b_1$）到 $i$ 有多少个环，用 dfs 预处理。要统计 $x$ 到 $y$ 有几个环，就计算 $su{m}_x+su{m}_y-2\ast su{m}_{\mathrm{lca}(x,y)}+(\mathrm{lca}(x,y)>n)$。原理：$su{m}_x+su{m}_y$ 包括了 $x$ 到 $\mathrm{lca}(x,y)$ 的环，$y$ 到 $\mathrm{lca}(x,y)$ 的环和 $\mathrm{lca}(x,y)$ 到根的环乘上 2。减掉两倍的 $\mathrm{lca}(x,y)$ 到根的环的数量之后还要再加上 $\mathrm{lca}(x,y)$ 的环。$\mathrm{lca}(x,y)$ 用倍增法就可以啦。

代码

温馨提示：一定要用 scanf，否则会 TLE（本人以为是找环太慢，换了一种写法 qwq）。找环过程建议手动模拟帮助理解。

#include<bits/stdc++.h>
using namespace std;
#define maxlog 18 
#define mod 1000000007 
int n,m,x,y,k,b[100005],sum[200005],tot;
int anc[200005][20],dep[200005];
vector<int> go[100005],e[200005],st;
long long mi[100005];
bool vis[100005];
void dfs(int ps,int fa){if(vis[ps]){bool flag=0;for(int i=0;i<st.size();i++){if(st[i]==ps) flag=1,tot++;if(flag) b[st[i]]=tot;}return;}vis[ps]=1;st.push_back(ps);for(auto g:go[ps]){if(g==fa) continue;dfs(g,ps);}st.pop_back();
}
void pre(int ps,int fa){//sum 和 LCA 的前处理sum[ps]=sum[fa]+(ps>n);dep[ps]=dep[fa]+1;anc[ps][0]=fa;for(int i=1;i<maxlog;i++)anc[ps][i]=anc[anc[ps][i-1]][i-1];for(auto g:e[ps]) if(g!=fa) pre(g,ps);
}
int lca(int x,int y){if(x==y) return x;if(dep[x]<dep[y]) swap(x,y);for(int i=maxlog-1;i>=0;i--)if(dep[anc[x][i]]>=dep[y]) x=anc[x][i];if(x==y) return x;for(int i=maxlog-1;i>=0;i--)if(anc[x][i]!=anc[y][i])x=anc[x][i],y=anc[y][i];return anc[x][0];
}
int main(){scanf("%d%d",&n,&m);tot=n;mi[0]=1;for(int i=1;i<=n;i++){mi[i]=mi[i-1]*2%mod;b[i]=i;}for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);go[x].push_back(y);go[y].push_back(x);}dfs(1,0);for(int i=1;i<=n;i++)for(auto g:go[i])if(b[i]!=b[g])e[b[i]].push_back(b[g]);pre(b[1],0);scanf("%d",&k);for(int i=1;i<=k;i++){scanf("%d%d",&x,&y);x=b[x],y=b[y];int z=lca(x,y);int res=sum[x]+sum[y]-2*sum[z]+(z>n);printf("%lld\n",mi[res]);}return 0;
}